[Python] Get used to Keras while implementing Reinforcement Learning (DQN)
Introduction
This article is a reminder of what I was addicted to when trying to modify the algorithm a little, such as customizing objective functions, adding optimizers, and multiple inputs, while proceeding with the implementation of reinforcement learning (DQN) using Keras. This is what I left behind. Therefore, it is a Keras Tips for beginners rather than a commentary article on DQN.
Execution environment
Python3.5.2 Keras 1.2.1 tensorflow 0.12.1
What is DQN
It's been over two years since DQN (DeepQ Network) was announced by DeepMind, so there are commentary articles and implementation samples everywhere, so I don't think detailed explanations here are necessary. I will. However, roughly speaking, it is a learning method that makes it possible to estimate the Q value directly from a moving image by approximating the Q function part of the reinforcement learning method called Q-Learning by deep learning. As a theory of DQN
-Reinforcement learning from zero to deep -Reinforcement learning starting with Python -I tried to confront artificial intelligence with all my strength (Theory) [Nico Nico Douga] -History of DQN + Deep Q-Network written in Chainer
The commentary articles around here are very polite and easy to understand, so please take a look there. Similar to other deep learning studies. Research on reinforcement learning has progressed at a stretch in the last few years, and DQN announced in 2013 is not the latest method, but since the algorithm is simple, easy to understand, and easy to implement, we will deal with it this time.
What is Keras
Keras is a deep learning wrapper library based on Theano and TensorFlow. Thanks to Theano and TensorFlow, it has become much easier to get into deep learning, but it is still difficult to write algorithms. So, Keras is a library that makes it possible to write a network structure quite simply. Even beginners of machine learning like me can write code relatively easily. If you are new to Keras, I wrote the basic part in the article Sine wave prediction using RNN in deep learning library Keras. , If you don't mind, please see that.
DQN implementation in Keras (Tensorflow)
There are many articles explaining DQN implementation in Keras and Tensorflow.
-Implementing DQN (complete version) with Tensorflow -DQN with TensorFlow-Artificial Intelligence Bug in Hakodate- -Implement DQN with Keras, TensorFlow and OpenAI Gym -Ultra-simple implementation of DQN (Deep Q Network) with TensorFlow ~ Introduction ~ -Write Reversi AI with Keras + DQN -I want DQN Puniki to hit a home run
So, if you know Keras and want to see the DQN implementation, I think you should read the above article.
Also, the algorithm implementation is good, and I want to try reinforcement learning with Keras quickly! For those who say, there is a keras library specializing in reinforcement learning called keras-rl, so please have a look there. About how to use [Python] Easy Reinforcement Learning (DQN) with Keras-RL I think that the article of is helpful.
Let's implement DQN with Keras very simply
I made a long introduction, but this is the main subject. This time, as I get used to Keras, I think it is easier to understand if I modify what was originally implemented in Tensorflow etc., so I will use the one that has already been implemented and published in Tensorflow. The chapter title remains the same, but ALGO GEEKS's Super Simple TensorFlow DQN (Deep Try to implement Q Network) ~ Introduction ~ I borrowed the code given in To do. It is a very compact and easy-to-understand implementation, and since the learning time is short and the results can be seen immediately, we will convert this to Keras.
The code implemented this time is given to github.
game

(State after turning 1000 epoch)
The learning environment is very simple, and as shown in the figure, it is a game in which you catch the falling balls one after another in the 8x8 square with the bar at the bottom. In implementing this time, the rules have been slightly changed from the original site.
--+1 reward for catching the ball --If you drop the ball -1 reward --Three types of actions (1: move to the right, 0: do not move, -1: move to the left) ――The place where the ball falls is random, the interval is 4 frames --The game is over when you drop the ball
It is.
Rewrite
In tensorflow
# input layer (8 x 8)
self.x = tf.placeholder(tf.float32, [None, 8, 8])
# flatten (64)
x_flat = tf.reshape(self.x, [-1, 64])
# fully connected layer (32)
W_fc1 = tf.Variable(tf.truncated_normal([64, 64], stddev=0.01))
b_fc1 = tf.Variable(tf.zeros([64]))
h_fc1 = tf.nn.relu(tf.matmul(x_flat, W_fc1) + b_fc1)
# output layer (n_actions)
W_out = tf.Variable(tf.truncated_normal([64, self.n_actions], stddev=0.01))
b_out = tf.Variable(tf.zeros([self.n_actions]))
self.y = tf.matmul(h_fc1, W_out) + b_out
# loss function
self.y_ = tf.placeholder(tf.float32, [None, self.n_actions])
self.loss = tf.reduce_mean(tf.square(self.y_ - self.y))
# train operation
optimizer = tf.train.RMSPropOptimizer(self.learning_rate)
self.training = optimizer.minimize(self.loss)
# saver
self.saver = tf.train.Saver()
# session
self.sess = tf.Session()
self.sess.run(tf.global_variables_initializer())
It was.

In the original DQN, after sandwiching 3 layers of Conv layer, Relu is applied by fully coupling, but this time the number of pixels is small as 8x8, and the Conv layer takes time to learn, so like this I think it has become. If you rewrite this with Keras
self.model = Sequential()
self.model.add(InputLayer(input_shape=(8, 8)))
self.model.add(Flatten())
self.model.add(Dense(32, activation='relu'))
self.model.add(Dense(self.n_actions))
optimizer=RMSprop(lr=self.learning_rate)
self.model.compile(loss='mean_squared_error',
optimizer=optimizer,
metrics=['accuracy'])
It looks like. The best thing about Keras is that the network code is fairly simple. Now you have a model that outputs 3 Q values for each action when you input 8x8 game screen pixels.
Use the predict function to get the Q value
def Q_values(self, states):
res = self.model.predict(np.array([states]))
return res[0]
It's okay, and the experience memory part is
# training
self.model.fit(np.array(state_minibatch), np.array(y_minibatch), batch_size=minibatch_size,nb_epoch=1,verbose=0)
It becomes. The save and load of the model are
def load_model(self, model_path=None):
yaml_string = open(os.path.join(f_model, model_filename)).read()
self.model = model_from_yaml(yaml_string)
self.model.load_weights(os.path.join(f_model, weights_filename))
self.model.compile(loss='mean_squared_error',
optimizer=RMSProp(lr=self.learning_rate),
metrics=['accuracy'])
def save_model(self, num=None):
yaml_string = self.model.to_yaml()
model_name = 'dqn_model{0}.yaml'.format((str(num) if num else ''))
weight_name = 'dqn_model_weights{0}.hdf5'.format((str(num) if num else ''))
open(os.path.join(f_model, model_name), 'w').write(yaml_string)
self.model.save_weights(os.path.join(f_model, weight_name))
It looks like. It's compact.
Since this implementation emphasized clarity and compactness, there are some differences from the original DQN.
--No target network --No clipping with loss function --Do not use convolution in the network --I am using normal RMS Prop as an optimizer, not RMS Prop Graves recommended by DQN -(Start learning after filling up the replay memory) -(Randomly decrease the rate of action selection from 1 regardless of the Q value)
This time, I will explain these points and the points that I got stuck when implementing with Keras.
Tips1: Copy the model
In DQN, in order not to overestimate the selected action, a measure is taken to separate the model used when performing experience memory (evaluating the action) and when selecting the action selection. In the original paper [1], both used the same model, and in the 2015 paper [2] published in nature, both were separated and a new target network was introduced. This will create a teacher signal using the old parameters, the explanation around here is
introduction to double deep Q-learning
It is explained in a very easy-to-understand manner, so please have a look there.
On the implementation side, once every few frames, you have to copy the model used for action selection and pass it to the target model. What to do with Keras
from keras.models import model_from_config
def clone_model(model, custom_objects={}):
config = {
'class_name': model.__class__.__name__,
'config': model.get_config(),
}
clone = model_from_config(config, custom_objects=custom_objects)
clone.set_weights(model.get_weights())
return clone
self.target_model = clone_model(self.model)
You can copy by passing the model and weight to the new model respectively.
However,
import copy
self.target_model = copy.copy(self.model)
##deepcopy results in an error
# self.target_model = copy.deepcopy(self.model)
It seems that the model and parameters are copied even with the standard copy function (I could not find it officially), but the behavior is a little scary, so the previous method is better.
This time, clone_model is used to periodically copy the current model to target_model, and target_model is used when evaluating and updating the Q value. (As an aside, in the improved version of DQN, DDQN, the Q value obtained by putting the state in the target model corresponds to A in search of'action that takes the maximum Q value obtained by putting the state in the current model'(A). I am using what I do)
def Q_values(self, states, isTarget=False):
model = self.target_model if isTarget else self.model
res = model.predict(np.array([states]))
return res[0]
def store_experience(self, states, action, reward, states_1, terminal):
self.D.append((states, action, reward, states_1, terminal))
return (len(self.D) >= self.replay_memory_size)
def experience_replay(self):
state_minibatch = []
y_minibatch = []
action_minibatch = []
# sample random minibatch
minibatch_size = min(len(self.D), self.minibatch_size)
minibatch_indexes = np.random.randint(0, len(self.D), minibatch_size)
for j in minibatch_indexes:
state_j, action_j, reward_j, state_j_1, terminal = self.D[j]
action_j_index = self.enable_actions.index(action_j)
y_j = self.Q_values(state_j)
if terminal:
y_j[action_j_index] = reward_j
else:
if not self.use_ddqn:
v = np.max(self.Q_values(state_j_1, isTarget=True))
else: # for DDQN
v = self.Q_values(state_j_1, isTarget=True)[action_j_index]
y_j[action_j_index] = reward_j + self.discount_factor * v
state_minibatch.append(state_j)
y_minibatch.append(y_j)
action_minibatch.append(action_j_index)
# training
self.model.fit(np.array(state_minibatch), np.array(y_minibatch), verbose=0)
Tips2: Customization of loss function
In the previous example,'mean_squared_error' was simply used, but in DQN, in order to improve the stability of learning, the value of the error target − Q (s, a; θ) is changed from -1 to 1. Clip in the range of. This area
Implement DQN with Keras, TensorFlow and OpenAI Gym
It is explained in a very easy-to-understand manner, so please have a look there.
Keras provides several types of loss functions by default, and you can use them just by writing a name like 'mean_squared_error', but there are times when you want to define the loss function yourself like this time.
Of course, Keras has a way to do that (although it's a bit tricky).
def loss_func(y_true, y_pred):
error = tf.abs(y_pred - y_true)
quadratic_part = tf.clip_by_value(error, 0.0, 1.0)
linear_part = error - quadratic_part
loss = tf.reduce_sum(0.5 * tf.square(quadratic_part) + linear_part)
return loss
self.model.compile(loss=loss_func, optimizer='rmsprops', metrics=['accuracy'])
You can define your own loss function like this (y_true is the teacher data and y_pred is the model output). This function is used when calling model.fit or model.evaluate.
[Reference] How to use a custom objective function for a model? # 369
It's a little tricky because it's very difficult to introduce external parameters other than y_true and y_pred into the loss function.
In this example, as the value to be assigned to y_true in experience memory, the output Q value list from the current model is assigned as it is (only the part with update is updated) ([1.2, 0.5, 0.1]-> [1.3". , 0.5, 0.1] ), The absolute value difference from the output Q value list from the current model is taken inside the loss function. Therefore, in ʻerror, the value remains only in the updated part, and the others are 0 ([1.3, 0.5, 0.1]-[1.2, 0.5, 0.1] = [0.1, 0, 0]`. ). In the end, only the updated part affects the loss value, and no other external variables are needed.
However, pass the teacher signal (update value only) (1.3), model output ([1.2, 0.5, 0.1] ), and selection action ( 0) to the loss function, and calculate the loss value from them in the model. As soon as you try to calculate, it becomes troublesome. In Tensorflow
state = tf.placeholder(tf.float32, [None, 8, 8]) #Status
a = tf.placeholder(tf.int64, [None]) #Action
supervisor = tf.placeholder(tf.float32, [None]) #Teacher signal
output = self.inference(state)
loss = lossfunc(output, supervisor)
...
loss_val = sess.run(loss, feed_dict={
self.state: np.float32(np.array(state_batch),
self.action: action_batch,
self.super_visor: y_batch
})
def lossfunc(self, a, output, supervisor)
a_one_hot = tf.one_hot(a, self.num_actions, 1.0, 0.0) #Convert behavior to one hot vector
q_value = tf.reduce_sum(tf.mul(output, a_one_hot), reduction_indices=1) #Calculation of Q value of behavior
#Error clip
error = tf.abs(supervisor - q_value)
quadratic_part = tf.clip_by_value(error, 0.0, 1.0)
linear_part = error - quadratic_part
loss = tf.reduce_mean(0.5 * tf.square(quadratic_part) + linear_part) #Error function
It's very simple like this, but Keras doesn't do that. What to do is to create a model that takes y_true, y_pred, and other external functions as inputs and outputs the loss value.
Tips3: Multiple inputs, multiple outputs
from keras.layers.core import Dense, Dropout, Activation, Flatten
from keras.layers import Lambda, Input
losses = {'loss': lambda y_true, y_pred: y_pred, #dummy loss func
'main_output': lambda y_true, y_pred: K.zeros_like(y_pred)}
def customized_loss(args):
import tensorflow as tf
y_true, y_pred, action = args
a_one_hot = tf.one_hot(action, K.shape(y_pred)[1], 1.0, 0.0)
q_value = tf.reduce_sum(tf.mul(y_pred, a_one_hot), reduction_indices=1)
error = tf.abs(q_value - y_true)
quadratic_part = tf.clip_by_value(error, 0.0, 1.0)
linear_part = error - quadratic_part
loss = tf.reduce_sum(0.5 * tf.square(quadratic_part) + linear_part)
return loss
...
def init_model(self):
state_input = Input(shape=(1, 8, 8), name='state')
action_input = Input(shape=[None], name='action', dtype='int32')
x = Flatten()(state_input)
x = Dense(32, activation='relu')(x)
y_pred = Dense(3, activation='linear', name='main_output')(x)
y_true = Input(shape=(1, ), name='y_true')
loss_out = Lambda(customized_loss, output_shape=(1, ), name='loss')([y_true, y_pred, action_input])
self.model = Model(input=[state_input, action_input, y_true], output=[loss_out, y_pred])
self.model.compile(loss=losses,
optimizer=RMSprop(lr=self.learning_rate),
metrics=['accuracy'])
slef.init_model()
...
res = model.predict({'state': np.array([states]),
'action': np.array([0]), #dummy
'y_true': np.array([[0] * self.n_actions]) #dummy
})
return res[1][0]
...
self.model.fit({'action': np.array(action_minibatch),
'state': np.array(state_minibatch),
'y_true': np.array(y_minibatch)},
[np.zeros([minibatch_size]),
np.array(y_minibatch)],
batch_size=minibatch_size,
nb_epoch=1,
verbose=0)
... overwhelmingly troublesome. Keras has a fairly simple mechanism by default, but if you try to do something a little different from that, it will become troublesome at once.
What has changed is that
--A new action_input has been added to the input. --y_true is also treated as input (three inputs) --I'm using Lambda, which is used to define my own layer, to calculate loss --The loss value and Q value are output as output.
It is a point. It's hard. This is unavoidable as long as it is not possible to make major customizations such as changing the arguments of the loss function. By the way, this method is described in the official Keras example (https://github.com/fchollet/keras/blob/master/examples/image_ocr.py).
As a point
--By using Lambda, you can freely design the input, the processing in the layer, and the shape of the output. --Names are used for input and output using name, and are used for prediction and fit. --When there are multiple outputs, the loss function can be applied to each. --Since the loss value is included in the output of the model, the loss function specified at model.compile can be a dummy, the function to be applied to the loss value outputs the value as it is, and the function to be applied to the Q value always outputs 0. It has become. --Specify a dummy value for the input that is not used when calling predict (unnecessary?), And treat the teacher signal as an input when calling fit.
What a place, such as. To be honest, there is a theory that it is better to use Tensorflow than to write like this, but if you write with Keras only, will it be like this? You can also use Keras for only the model set and Tensorflow for the rest.
Tips4: Change optimizer
Since the article has become longer than I expected, I will omit a detailed explanation (maybe I will add it later?), But in DQN, it is said that performance is likely to come out if RMS PopGraves is used as the optimizer instead of the usual RMS Drop. I'm a beginner in machine learning, so I'm not sure why it's faster when I look at the formula (please tell me ...), but if it's faster to learn, I definitely want to use it (except for DQN + RNN papers, etc.) It seems that you are using the optimizer of). However, this RMSPropsGraves is included in Chainer by default, but it is not included in Tensorflow and Keras (I have not tried it, but it may be usable if it is Keras in the Chainer background). Therefore, you need to implement optimizer yourself. Tensorflow version
Implementing DQN (complete version) with Tensorflow
Please refer to the detailed explanation here. It can be implemented by looking at the formula in the paper [3].
The difference in the transition of the loss value when epoch is repeated is as follows.
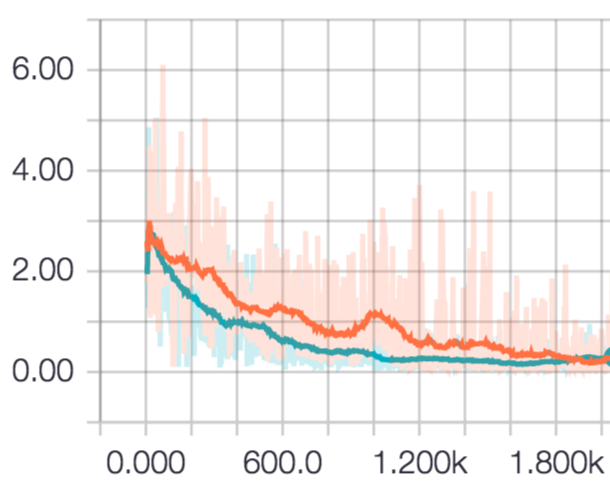
Red is the one turned by RMS Prop, and blue is the one turned by RMS Prop Graves. At first, RMS PopGraves seemed to be superior, but after turning 2000 times, both settled down to the same level. It may be because the task was easy.
In Keras, the definition of optimizer is all in https://github.com/yukiB/keras/blob/master/keras/optimizers.py, so it seems good to rewrite it. Regarding WIP, I will give the code to github.
Try in a slightly more complicated game
The performance of the Oita model should have improved so far, so let's increase the number of pixels and add three Conv layers before full coupling.

The result of turning 1000 times is as follows.

Next, let's make a slightly more complicated game and use the same model for learning. I easily implemented a game called CAVE, which I played very much during the feature phone era, with matplotlib. This is a game in which the urine that rises when the button is pressed and descends when released is advanced so as not to hit the wall as much as possible.
The game screen is 48x48, using the network (Conv3 layer + fully connected Relu) created earlier,
--Input: Downsampled last 4 frames --Output: Button input (ON, OFF)
I made it so that.
As a result, I rarely hit the upper and lower walls, but I didn't learn much about avoiding blocks along the way, and my score didn't improve. For the time being, 4 frames are taken as input data, but depending on the positional relationship between blocks, it is possible that more retroactive frame data will be effective, so it may be better to consider DQN etc. combined with LSTM. not. I will talk about this again next time

(It's dangerous because the time has passed infinitely just by looking at the learning results)
in conclusion
This time, when building DQN with Keras, I picked up the places where beginners are likely to stumble. I dealt with DQN this time because it was my first reinforcement learning, but I'm quite behind the times (the combination of DDQN and LSTM is still active), so next time I'd like to use A3C etc. I think.
The code for this time can be found at here.
References
[1] V. Mnih, K. Kavukcuoglu, D. Silver, A. Graves I. Antonoglou, D. Wierstra, M. Riedmiller. “Playing Atari with Deep Reinforcement Learning” arXiv:1312.5602, 2013. [2] V. Mnih, et al. “Human-level control through deep reinforcement learning” nature, 2015. [3] Alex Graves, “Generating Sequences With Recurrent Neural Networks” arXiv preprint arXiv http://arxiv.org/abs/1308.0850
Recommended Posts