First posted an article as a job hunting story.

I read and implemented an unsupervised learning, IIC (Invariant Information Clustering) paper, which is said to be highly accurate. IIC is a method of clustering by maximizing the amount of mutual information. The IIC paper is here

Invariant Information Clustering for Unsupervised Image Classification and Segmentation Xu Ji, João F. Henriques, Andrea Vedaldi

The framework used is TensorFlow 2.0. The target data is the familiar MNIST.

About mutual information

There are multiple interpretations of mutual information, but we will choose a simple method that is easy to explain this machine learning.

The information entropy H (X) for the probability distribution X is defined below.

H(X) = -\sum_{i}x_{i} \ln x_{i}

This amount increases as the distribution is closer to a uniform distribution, and becomes 0 when the distribution converges to one point. The mutual information $ I $ can be said to be the amount in which the sets of information entropies of two ** non-independent ** probability distributions $ X $ and $ Y $ match.

I(X, Y) = H(X) + H(Y) - H(X,Y)

As you can see from the figure, maximizing the mutual information amount $ I $ brings the information entropy of $ X $ and $ Y $ closer, and increases the information entropy of $ X $ and $ Y $. By bringing the information entropy closer, the expression learning of the network progresses, and by increasing the information entropy, there is an effect of preventing clustering from concentrating on one point (degeneration).

In actual learning, when the softmax output from the network for an image pair ($ X $, $ X') is ( Z $, $ Z'$), the simultaneous probability of $ Z $, $ Z'$ is calculated. Maximizes the mutual information about the marginal probabilities $ P_ {x}, P_ {y} $ of the symmetrized matrix $ P $. The specific formula of the loss function is as follows.

\begin{align}
I(P_{x}, P_{y}) &= -\sum_{i}P_{x(i)} \ln P_{x(i)}-\sum_{j}P_{y(j)} \ln P_{y(j)}+\sum_{i}\sum_{j}P_{(i, j)} \ln P_{(i, j)}\\
&=\sum_{i}\sum_{j}\bigl(P_{(i, j)}(-\ln P_{x(i)}-\ln P_{y(j)}+\ln P_{(i, j)})\bigr)\\
&=\sum_{i}\sum_{j}P_{(i, j)}・\ln \frac{P_{(i, j)}}{P_{x(i)} P_{y(j)}}
\end{align}

Make a pair of images

For learning, it is necessary to make a pair of $ X'$ for the image $ X $. $ X $ and $ X'$ are pairs of data that contain the same object, but it is desirable that the instance-specific details are different. The point is that the network outputs $ Z and Z'$ are highly dependent and not independent because they are the same pair of objects.

Generally, $ X $ is made into $ X'$ by adding operations such as scaling, skewing (distorting), rotation, inversion, and changing contrast and saturation. This time, the following 4 operations were performed.

Original image	Rotation	distortion	Binarization	Noise

This operation will greatly affect learning.

Network structure

Needless to say, it is better to do transfer learning, but this time it is a simple task, so I simply made a familiar form of Conv and BN. Outputs a softmax prediction vector for an input 28x28x1 image. Output $ Z $ is MNIST clustering, 10 dimensions equal to the number of labels. The other is the output used in a technique called Overclustering in the paper, which is 50 dimensions, which is five times the label. Overclustering is a mechanism in which the network acquires more features by simultaneously performing more clustering than the expected number of clustering. The convolution layer weights are shared for these two learnings, but the fully connected layers use different weights.

def create_model(self):
    inputs = layers.Input((28,28,1))

    x = layers.Conv2D(32, 3, padding="same")(inputs)
    x = layers.BatchNormalization()(x)
    x = layers.Activation("relu")(x)
    x = layers.MaxPooling2D(2)(x)

    x = layers.Conv2D(64, 3, padding="same")(x)
    x = layers.BatchNormalization()(x)
    x = layers.Activation("relu")(x)
    x = layers.MaxPooling2D(2)(x)

    x = layers.Conv2D(128, 3, padding="same")(x)
    x = layers.BatchNormalization()(x)
    x = layers.Activation("relu")(x)
    x = layers.MaxPooling2D(2)(x)

    x = layers.Conv2D(256, 3, padding="same")(x)
    x = layers.BatchNormalization()(x)
    x = layers.Activation("relu")(x)
    conv_out = layers.GlobalAveragePooling2D()(x)

    x = layers.Dense(128, activation="relu")(conv_out)
    x = layers.Dense(64, activation="relu")(x)
    Z = layers.Dense(10, activation="softmax")(x)

    x = layers.Dense(128, activation="relu")(conv_out)
    x = layers.Dense(64, activation="relu")(x)
    overclustering = layers.Dense(50, activation="softmax")(x)

    return Model(inputs, [Z, overclustering])

Definition of loss function

Give the model batch data of image pairs $ X, X'$, get the output of $ Z, Z'$ and Overclustering, and perform mutual information calculation for each with the IIC method. The paper has an implementation example in Pytrch, and when rewritten to TenosrFlow 2.0, it becomes the following code. We aim to maximize the amount of mutual information, but since machine learning minimizes it, we multiply the entire loss function by a minus. The final loss is the average of clustering and overclustering, and the gradient is calculated with this value.

def IIC(self, z, z_, c=10):
    z = tf.reshape(z, [-1, c, 1])
    z_ = tf.reshape(z_, [-1, 1, c])
    P = tf.math.reduce_sum(z * z_, axis=0)  #Simultaneous probability
    P = (P + tf.transpose(P)) / 2  #Symmetrization
    P = tf.clip_by_value(P, 1e-7, tf.float32.max)  #Bias to prevent log divergence
    P = P / tf.math.reduce_sum(P)  #Standardization
    
    #Peripheral probability
    Pi = tf.math.reduce_sum(P, axis=0)
    Pi = tf.reshape(Pi, [c, 1])
    Pi = tf.tile(Pi, [1,c])
    Pj = tf.math.reduce_sum(P, axis=1)
    Pj = tf.reshape(Pj, [1, c])
    Pj = tf.tile(Pj, [c,1])

    loss = tf.math.reduce_sum(P * (tf.math.log(Pi) + tf.math.log(Pj) - tf.math.log(P)))

    return loss

@tf.function
def train_on_batch(self, X, X_):
    with tf.GradientTape() as tape:
        z, overclustering = self.model(X, training=True)
        z_, overclustering_ = self.model(X_, training=True)
        loss_cluster = self.IIC(z, z_)
        loss_overclustering = self.IIC(overclustering, overclustering_, c=50)

        loss = (loss_cluster + loss_overclustering) / 2

    graidents = tape.gradient(loss, self.model.trainable_weights)
    self.optim.apply_gradients(zip(graidents, self.model.trainable_weights))
    return loss_cluster, loss_overclustering

Learning results

Learning parameters optimizer is Adam's rate 0.0001 batch_size is 1000 The results of learning up to epoch100 using the image pairs in each conversion operation are as follows.

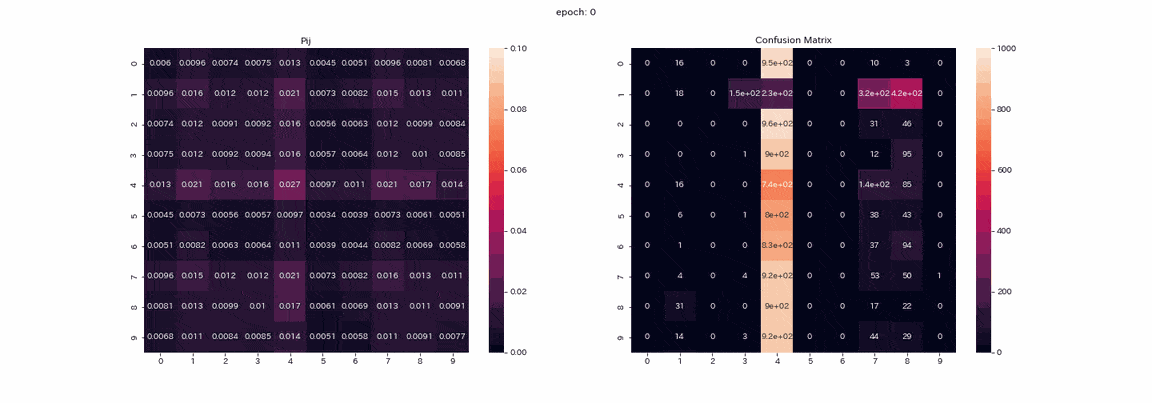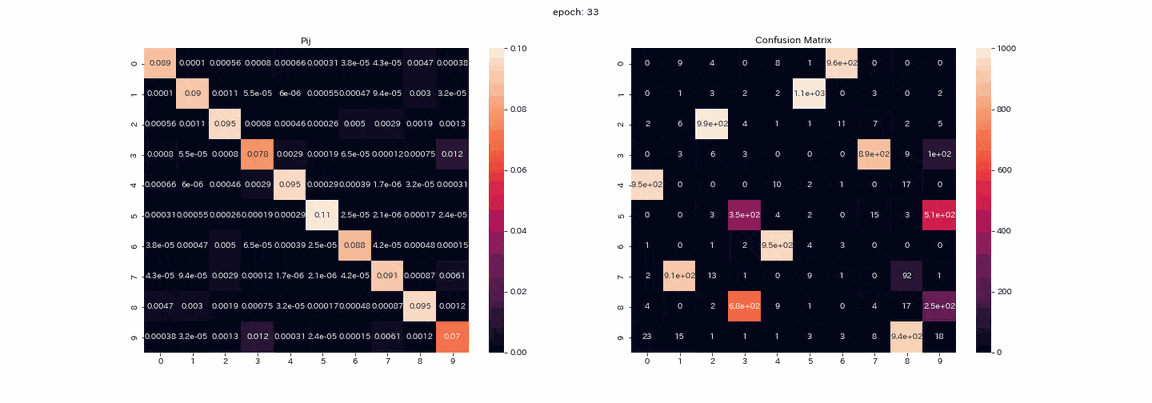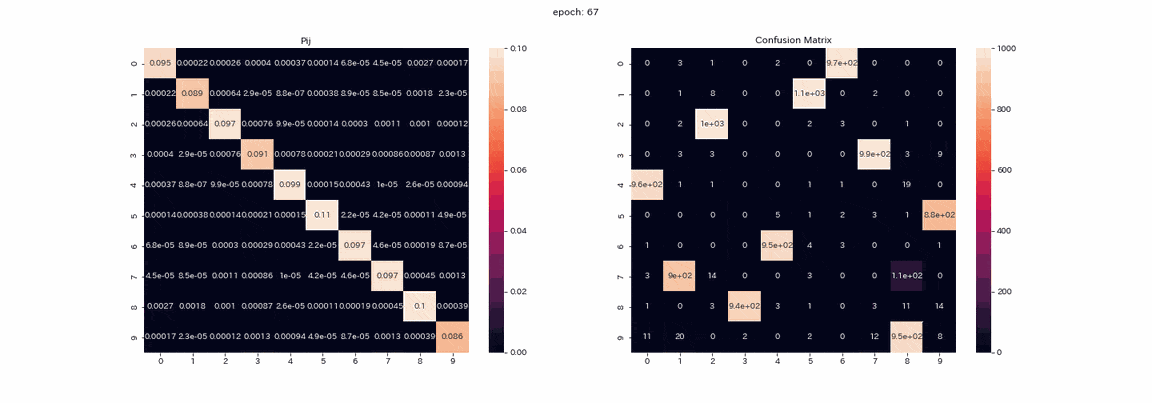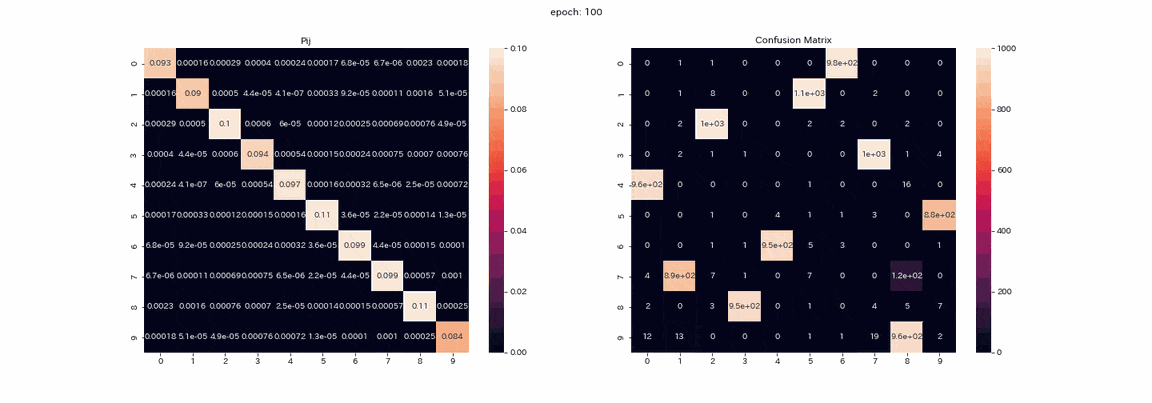
Looking at the graph, we can see that it is better to combine multiple conversions than to perform the conversion alone. The following is training with an image pair that has undergone all four transformations with the best results. The matrix $ P $ being trained and the mixed matrix of test data prediction (vertical axis is the true label, horizontal axis is the output index). ) Is a recorded gif.

Actually, I learned more than 500 epochs, but I think that the learning was almost completed because there was not much change in more than 100 epochs. In the matrix $ P $, the values are arranged diagonally as the learning progresses, because $ Z and Z'$ will output the same distribution. You can also see that the value in column 1 is higher than the others. Labels 2 and 3 cannot be distinguished in the mixed matrix, and there are two columns that output label 8. Although not perfect, the accuracy rate was 85% without a teacher.

Improvement

Now, it is a good idea to find a conversion that makes better $ X'$ in order to increase the accuracy rate, but we will improve the accuracy by devising the loss function. Looking at the learning process earlier, it seems that the cause of the clustering error is that the peripheral probabilities of the matrix $ P $ are not even. If you check the mutual information formula, you can see that the terms $ H (X) and H (Y) $ equalize the marginal probabilities. Therefore, I decided to add a weight alpha to this section and use it as a parameter.

    #loss plus alpha
    loss = tf.math.reduce_sum(P * (alpha * tf.math.log(Pi) + alpha * tf.math.log(Pj) - tf.math.log(P)))

The result of learning with alpha set to 10 is as follows.

![rsbn_loss_matrix-compressor.gif](https://qiita-image-store.s3.ap-northeast-1.amazonaws.com/0/340563/7c501a33-c153-b365-5d7e-7e8cea89fa58.gif)

Learning is stable and almost all clustering is successful. The highest accuracy rate was about 97.5%, which was quite accurate.

bonus

I was curious about what kind of classification Overclustering is, so check it. Below is the mixed matrix of Overclustering (50 dimensions) in the most accurate model. It can be confirmed that all labels can be classified here as well. A part of columns 9, 23, 40 of label 7 is displayed.

Column 9	Column 23	Column 40

Each captures the characteristics of how to write "7". Is the difference between column 9 and column 40 the thickness of the line? When I looked up other numbers, the clusters were often separated by the difference in thickness, but this seems to be due to the nature of the convolution layer. It is column 23 that I would like to pay attention to. I checked everything, but almost all of the "7" I wrote in two strokes, which I'm not familiar with, fit in column 23. I felt that being able to classify and retrieve this "7" has the potential to create new labels beyond the teacher data.

The IIC paper shows that it is a method that can also be applied to segmentation, and it seems that it can be applied to various tasks as long as mutual information can be calculated. It was a method full of romantic performance that did not require teacher data.

A simple method to get MNIST correct answer rate of 97% or more by unsupervised learning (without transfer learning)