Linear regression with statsmodels
I used to use scipy.stats.linregress as a linear regression in Python, but I introduced statsmodels because it has few functions and is difficult to use. I've only used it for 2 hours, so I may have misunderstood something fundamentally. I've only used it for 2 hours, so I'm sorry.
The following describes how to use OLS (ordinary least square) of statsmodels. Click here for official materials http://statsmodels.sourceforge.net/stable/regression.html
Installation
Normally with pip.
$ sudo pip install statsmodels
The code below also uses numpy and matplotlib, so install them if you don't have them.
$ sudo pip install numpy
$ sudo pip install matplotlib
Simple example
For the time being, as the simplest example
y = a + bx + \varepsilon
Consider linear regression in the model. In other words, given the data of $ (x_i, y_i) $, the parameter $ (a, b) $ is determined so that the error $ \ sum \ varepsilon_i ^ 2 $ is minimized.
For example, suppose you have the following data. This is the data I made now, and if I answered first, it would be a = 1.0, b = 3.0, but I pretend I don't know and find it by regression.
data.txt
# x y
-1.000 -1.656
-0.900 -0.734
-0.800 -3.036
-0.700 -1.026
-0.600 -1.104
-0.500 0.023
-0.400 0.246
-0.300 1.817
-0.200 0.651
-0.100 0.082
-0.000 2.524
0.100 2.231
0.200 0.783
0.300 2.489
0.400 1.892
0.500 3.207
0.600 1.868
0.700 3.954
0.800 4.447
0.900 4.024
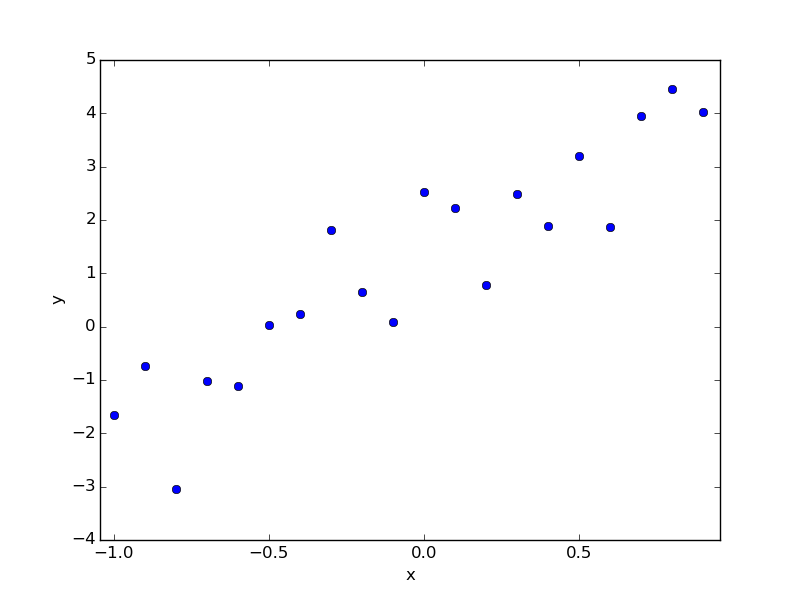
The regression for this is as follows.
regression.py
# coding: utf-8
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
#Read data
data = np.loadtxt("data.txt")
x = data.T[0]
y = data.T[1]
#Number of samples
nsample = x.size
#Magic(Commentary later)
X = np.column_stack((np.repeat(1, nsample), x))
#Regression execution
model = sm.OLS(y, X)
results = model.fit()
#View result summary
print results.summary()
#Get parameter estimates
a, b = results.params
#Show plot
plt.plot(x, y, 'o')
plt.plot(x, a+b*x)
plt.text(0, 0, "a={:8.3f}, b={:8.3f}".format(a,b))
plt.show()
When executed, the following text and graph will be displayed.
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.831
Model: OLS Adj. R-squared: 0.822
Method: Least Squares F-statistic: 88.59
Date: Thu, 25 Dec 2014 Prob (F-statistic): 2.25e-08
Time: 14:07:16 Log-Likelihood: -24.450
No. Observations: 20 AIC: 52.90
Df Residuals: 18 BIC: 54.89
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------------------------------------------
const 1.2922 0.194 6.647 0.000 0.884 1.701
x1 3.1611 0.336 9.412 0.000 2.455 3.867
==============================================================================
Omnibus: 0.801 Durbin-Watson: 2.495
Prob(Omnibus): 0.670 Jarque-Bera (JB): 0.653
Skew: -0.402 Prob(JB): 0.721
Kurtosis: 2.628 Cond. No. 1.74
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

It will be like this.
Linear basis function model
In the model mentioned above, the relationship between x and y was a linear expression, but in life we often want to consider a more complicated relationship between x and y. Therefore, by using a linear basis function model, it becomes possible to express a relatively diverse relationship between x and y.
y = \beta_0 + \beta_1 \phi_1(x) + \beta_2\phi_2(x) + \cdots + \beta_{M-1}\phi_{M-1}(x) + \varepsilon
Here, $ x and y $ are data, $ \ phi_j (x) $ is a known function, and $ \ beta_j $ is a parameter to be obtained. Note that this formula can be easily set to $ \ phi_0 (x) \ equiv 1 $.
y = \sum_{j=0}^{M-1} \beta_j\phi_j(x) + \varepsilon
Can also be written. For example, if $ M = 3, \ phi_1 (x) = x, \ phi_2 (x) = x ^ 2 $, then the quadratic function $ y = \ beta_0 + \ beta_1x + \ beta_2x ^ 2 + \ varepsilon $ ..
When performing regression with statsmodels, you need to enter the data $ (x_i, y_i) $ and the information of the known function $ \ phi_j (x) $, but it is awkward to insert the function information directly, so $ Enter the following matrix that summarizes the information of x_i $ and $ \ phi_j (x_i) $. (When M = 3)
X = \begin{Bmatrix}
\phi_0(x_0) & \phi_1(x_0) & \phi_2(x_0) \\
\phi_0(x_1) & \phi_1(x_1) & \phi_2(x_1) \\
\phi_0(x_2) & \phi_1(x_2) & \phi_2(x_2) \\
& \vdots & \\
\end{Bmatrix}
Here, $ \ phi_0 (x) \ equiv 1 $, so the first column of this matrix is all 1. That's why I added the column `` `np.repeat (1, nsample) ``` in the previous code as "magic".
So, if we change the way this matrix X is created, linear regression of any model is possible.
Somewhat complicated example
As an example
y = a + bx + cx^2 + \varepsilon
Consider the model. All you have to do is add a column corresponding to $ x ^ 2 $ to the matrix X part of the previous code. First, prepare the data set. As usual, the answer is a = 3.0, b = 1.0, c = 2.0.
data.txt
# x y
-2.000 10.260
-1.800 7.403
-1.600 7.779
-1.400 4.310
-1.200 4.051
-1.000 4.577
-0.800 3.416
-0.600 3.628
-0.400 3.968
-0.200 3.780
-0.000 1.873
0.200 2.741
0.400 2.106
0.600 5.286
0.800 8.138
1.000 5.316
1.200 9.159
1.400 9.748
1.600 7.585
1.800 10.726
The code is below. However, I changed only the part where the matrix X was created and the number of the last parameters.
regression_2.py
# coding: utf-8
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
#Data read
data = np.loadtxt("data.txt")
x = data.T[0]
y = data.T[1]
#Number of samples
nsample = x.size
#Creating matrix X
X = np.column_stack((np.repeat(1, nsample), x, x**2))
#Perform regression
model = sm.OLS(y, X)
results = model.fit()
#View result summary
print results.summary()
#Get parameter estimates
a, b, c = results.params
#Display as a graph
plt.plot(x, y, 'o')
plt.plot(x, a+b*x+c*x**2)
plt.title("a={:.4f}, b={:.4f}, c={:.4f}".format(a,b,c))
plt.show()
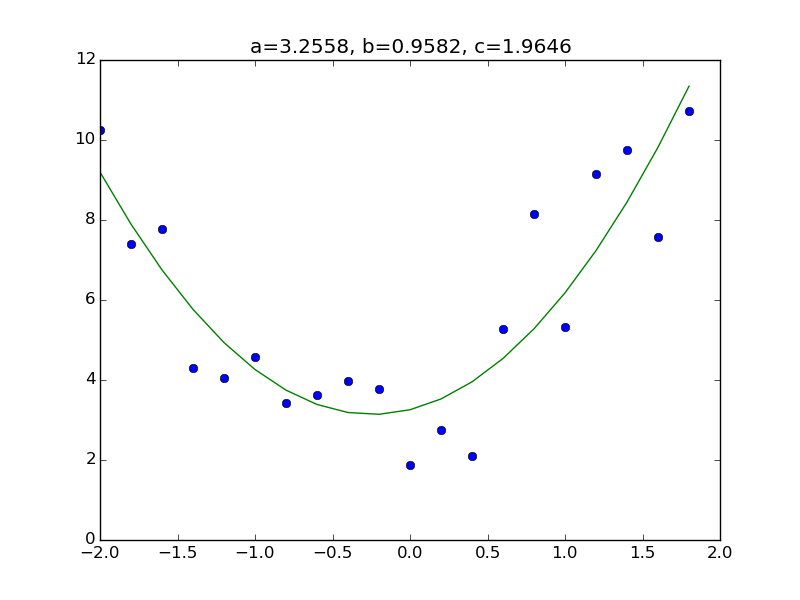
Other
In addition to OLS (ordinary least squares), statsmodels also has WLS (weighted least squares), so write it if you like.
Recommended Posts