2. Multivariate analysis spelled out in Python 7-2. Decision tree [difference in division criteria]
- There are several classification criteria for decision trees.
- Commonly used are two impurity measurements, gini impurities and entropy, and a division criterion called misclassification error.
- Let's see these differences.
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
Comparison of each index in 2 class classification
- In 2 class classification, if the ratio of one class is p, each index can be calculated as follows.
- ** Gini: $ 2p * (1-p) $ **
- ** entropy: $ -p * \ log p-(1-p) * log (1-p) $ **
- ** misclassification rate: $ 1-max (p, 1-p) $ **
#Generate arithmetic progression corresponding to p
xx = np.linspace(0, 1, 50) #Start value 0, end value 1, number of elements 50
plt.figure(figsize=(10, 8))
#Calculate each index
gini = [2 * x * (1-x) for x in xx]
entropy = [-x * np.log2(x) - (1-x) * np.log2(1-x) for x in xx]
misclass = [1 - max(x, 1-x) for x in xx]
#Show graph
plt.plot(xx, gini, label='gini', lw=3, color='b')
plt.plot(xx, entropy, label='entropy', lw=3, color='r')
plt.plot(xx, misclass, label='misclass', lw=3, color='g')
plt.xlabel('p', fontsize=15)
plt.ylabel('criterion', fontsize=15)
plt.legend(fontsize=15)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.grid()
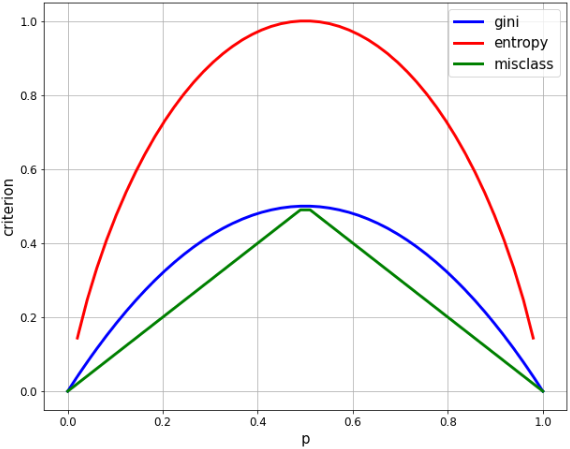
- When the ratio of 2 classes is equal (p = 0.5), both are the maximum values,
- The maximum entropy is 1.0 and the gini is 0.5, so scale the entropy by a factor of 1/2 for ease of comparison.
#Generate arithmetic progression corresponding to p
xx = np.linspace(0, 1, 50) #Start value 0, end value 1, number of elements 50
plt.figure(figsize=(10, 8))
#Calculate each index
gini = [2 * x * (1-x) for x in xx]
entropy = [(x * np.log((1-x)/x) - np.log(1-x)) / (np.log(2)) for x in xx]
entropy_scaled = [(x * np.log((1-x)/x) - np.log(1-x)) / (2*np.log(2)) for x in xx]
misclass = [1 - max(x, 1-x) for x in xx]
#Show graph
plt.plot(xx, gini, label='gini', lw=3, color='b')
plt.plot(xx, entropy, label='entropy', lw=3, color='r', linestyle='dashed')
plt.plot(xx, entropy_scaled, label='entropy(scaled)', lw=3, color='r')
plt.plot(xx, misclass, label='misclass', lw=3, color='g')
plt.xlabel('p', fontsize=15)
plt.ylabel('criterion', fontsize=15)
plt.legend(fontsize=15)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.grid()
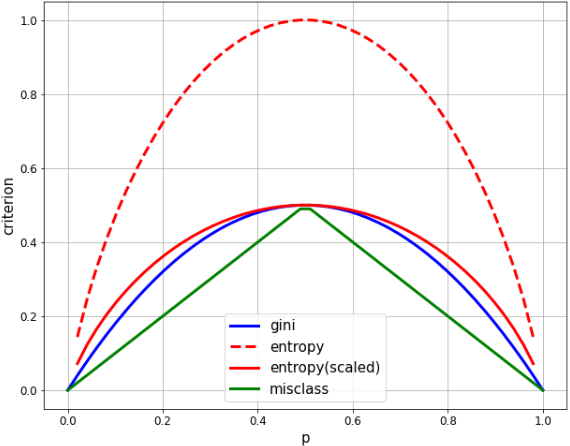
- Gini and entropy are very similar, both drawing a quadratic curve and maximizing at p = 1/2.
- Misclasses are clearly different in that they are linear, but they share many of the same characteristics. It maximizes at p = 1/2, equals zero at p = 0, 1, and changes in a mountain.
Differences in each index in information gain
1. What is information gain?
- ** Information gain ** is an index that shows how much the impureness decreased before and after the division when the data was divided using a certain variable.
- The less impure, the more useful the variable is as a classification condition.
- In that sense, how to reduce the impureness is synonymous with ** maximizing the information gain at each branch **.
- For two-class classification, ** information gain (IG) ** is defined in the following equation.
\displaystyle IG(D_{p}, a) = I(D_{p}) - \frac{N_{left}}{N} I(D_{left}) - \frac{N_{right}}{N} I(D_{right}) - $ I $ means impure, $ D_ {p} $ is the data of the parent node, the left and right of the data of the child node are $ D_ {left} $ and $ D_ {right} $, and the parent The left and right ratios of the child nodes are based on the number of node samples $ N $ as the denominator.
2. Calculate the information gain for each index
- Assume the following two branch conditions A and B.
- Compare the information gain between branching conditions A and B for each of gini, entropy, and misclassification rate.
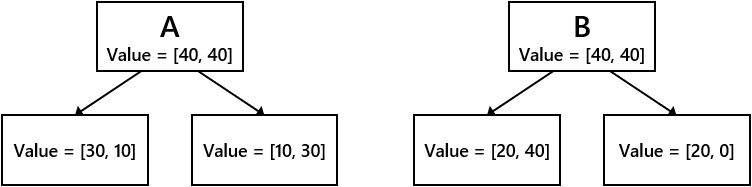
➀ Information gain due to Gini impure
#Gini purity of parent node
IGg_p = 2 * 1/2 * (1-(1/2))
#Gini purity of child node A
IGg_A_l = 2 * 3/4 * (1-(3/4)) #left
IGg_A_r = 2 * 1/4 * (1-(1/4)) #right
#Gini impureness of child node B
IGg_B_l = 2 * 2/6 * (1-(2/6)) #left
IGg_B_r = 2 * 2/2 * (1-(2/2)) #right
#Information gain of each branch
IG_gini_A = IGg_p - 4/8 * IGg_A_l - 4/8 * IGg_A_r
IG_gini_B = IGg_p - 6/8 * IGg_B_l - 2/8 * IGg_B_r
print("Information gain of branch A:", IG_gini_A)
print("Information gain of branch B:", IG_gini_B)

➁ Information gain from entropy
#Parent node entropy
IGe_p = (4/8 * np.log((1-4/8)/(4/8)) - np.log(1-4/8)) / (np.log(2))
#Entropy of child node A
IGe_A_l = (3/4 * np.log((1-3/4)/(3/4)) - np.log(1-3/4)) / (np.log(2)) #left
IGe_A_r = (1/4 * np.log((1-1/4)/(1/4)) - np.log(1-1/4)) / (np.log(2)) #right
#Entropy of child node B
IGe_B_l = (2/6 * np.log((1-2/6)/(2/6)) - np.log(1-2/6)) / (np.log(2)) #left
IGe_B_r = (2/2 * np.log((1-2/2+1e-7)/(2/2)) - np.log(1-2/2+1e-7)) / (np.log(2)) #right,+1e-7 adds a small value to avoid division by zero
#Information gain of each branch
IG_entropy_A = IGe_p - 4/8 * IGe_A_l - 4/8 * IGe_A_r
IG_entropy_B = IGe_p - 6/8 * IGe_B_l - 2/8 * IGe_B_r
print("Information gain of branch A:", IG_entropy_A)
print("Information gain of branch B:", IG_entropy_B)
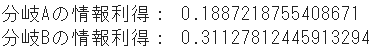
➂ Information gain due to misclassification rate
#Misclassification rate of parent node
IGm_p = 1 - np.maximum(4/8, 1-4/8)
#Misclassification rate of child node A
IGm_A_l = 1 - np.maximum(3/4, 1-3/4) #left
IGm_A_r = 1 - np.maximum(1/4, 1-1/4) #right
#Misclassification rate of child node B
IGm_B_l = 1 - np.maximum(2/6, 1-2/6) #left
IGm_B_r = 1 - np.maximum(2/2, 1-2/2) #right
#Information gain of each branch
IG_misclass_A = IGm_p - 4/8 * IGm_A_l - 4/8 * IGm_A_r
IG_misclass_B = IGm_p - 6/8 * IGm_B_l - 2/8 * IGm_B_r
print("Information gain of branch A:", IG_misclass_A)
print("Information gain of branch B:", IG_misclass_B)
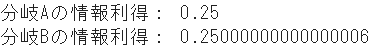
Summary
| Classification condition A | Classification condition B | |
|---|---|---|
| Gini Impure | 0.125 | 0.167 |
| Entropy | 0.189 | 0.311 |
| Misclassification rate | 0.250 | 0.250 |
- It is clear that classification condition B has priority for both gini and entropy. In fact, the results will be very similar.
- On the other hand, in the misclassification rate, classification conditions A and B are almost the same.
- In this way, the misclassification rate tends not to take a clear difference between variables, so sklearn's decision tree model uses two division criteria, gini and entropy (it seems).
- In addition, Gini may be a little faster because there is no logarithmic calculation like entropy.
Recommended Posts