Combinatorial optimization-typical problem-shortest path problem
Typical problem and execution method
Shortest path problem
When $ e_ {ij} = (v_i, v_j) \ in E $ has a weight of $ a_ {ij} $ on each side of the graph $ G = (V, E) $, the start point $ v_s \ in V $ to the end point $ Find the one with the smallest sum of weights on the way to v_t \ in V $.
Execution method
usage
Signature: nx.dijkstra_path(G, source, target, weight='weight')
Docstring:
Returns the shortest path from source to target in a weighted graph G.
python
#CSV data
import pandas as pd, networkx as nx
from ortoolpy import graph_from_table
tbn = pd.read_csv('data/node0.csv')
tbe = pd.read_csv('data/edge0.csv')
g = graph_from_table(tbn, tbe)[0]
print(nx.dijkstra_path(g, 5, 2))
result
[5, 4, 0, 2]
python
# pandas.DataFrame
from ortoolpy.optimization import DijkstraPath
DijkstraPath('data/edge0.csv', 5, 2)
| node1 | node2 | capacity | weight | |
|---|---|---|---|---|
| 9 | 4 | 5 | 2 | 1 |
| 3 | 0 | 4 | 2 | 2 |
| 1 | 0 | 2 | 2 | 4 |
python
#Random number data
import networkx as nx
g = nx.fast_gnp_random_graph(8, 0.26, 1)
print(nx.dijkstra_path(g, 0, 2))
result
[0, 1, 6, 3, 5, 2]
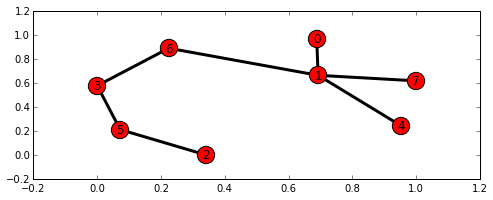
data
Recommended Posts