Acoustic signal processing with Python
This is the article on the 13th day of Python Part 2 Advent Calendar 2015. My usual work is mainly developing algorithms for acoustic signal processing and implementing DSPs, but when building algorithms, I first examine the algorithms using Python, and based on the results, C and C ++ The flow is to create a real-time model that runs on a PC. Surprisingly, there is no comprehensive Japanese article on acoustic signal processing, so here I would like to appropriately summarize how to perform acoustic signal processing with Python and the know-how that I have used in my work so far.
table of contents
- Motivation to process acoustic signals with Python
- Reading and writing audio files
- I want to perform audio processing in real time
- I want to display the frequency response
- I want to design a digital filter
- I want to convert zeros, poles and coefficient arrays b, a
- I want to apply a digital filter to a time series signal
- I want to calculate the group delay
- I want to calculate the time correlation (cross-correlation function)
- I want to detect a peak
Motivation to process acoustic signals with Python
An alternative to matlab. To be honest, matlab is treated as a fixed asset because it costs more than 200,000 for commercial use, and it is difficult to handle or the company cannot buy it in the first place, so I want to do something for free.
Reading and writing audio files
For how to read and write audio files, see the article 108 ways to handle wav files with python that I wrote on my blog in the past. It is summarized. Personally, I've been using PySoundFile more often these days. The following is the process of FFTing with 1/2 overlap, IFFTing, and restoring.
#!/usr/bin/env python
# vim:fileencoding=utf-8
import sys
import numpy as np
import scipy.fftpack as fft
import matplotlib.pyplot as plt
import soundfile as sf
if __name__ == '__main__':
plt.close("all")
#wav file reading
filename = sys.argv[1]
wav, fs = sf.read(filename)
#In the case of stereo 2ch, it is divided into Lch and Rch
wav_l = wav[:, 0]
wav_r = wav[:, 1]
#Monaural input
xs = (0.5 * wav_l) + (0.5 * wav_r)
n_len = len(xs)
n_fft = 128
n_overlap = 2
n_shift = n_fft / n_overlap
#Intermediate buffer
zs = np.zeros(n_len)
Zs = np.zeros(n_fft)
#Output buffer
ys = np.zeros(n_len)
#Window function
window = np.hanning(n_fft)
# FFT & IFFT
for start in range(0, n_len - n_shift, n_shift):
xs_cut = xs[start: start + n_fft]
xs_win = xs_cut * window
Xs = fft.fft(xs_win, n_fft)
# some signal processing
Zs = Xs
zs = fft.ifft(Zs, n_fft)
# write output buffer
ys[start: start + n_fft] += np.real(zs)
#10 seconds plot from the beginning
fig = plt.figure(1, figsize=(8, 10))
ax = fig.add_subplot(211)
ax.plot(xs[:fs*10])
ax.set_title("input signal")
ax.set_xlabel("time [pt]")
ax.set_ylabel("amplitude")
ax = fig.add_subplot(212)
ax.plot(ys[:fs*10])
ax.set_title("output signal")
ax.set_xlabel("time [pt]")
ax.set_ylabel("amplitude")
plt.show()
Plot example

I want to perform audio processing in real time
It's easy to use PortAudio's Python binding PyAudio.
Here is an example of buffering the microphone input signal in a global variable in the callback method and saving it in a wav file. First, list the available devices.
pyaudio_print_devices.py
#!/usr/bin/env python
# vim:fileencoding=utf-8
import pyaudio as pa
if __name__ == "__main__":
#List available devices
p_in = pa.PyAudio()
print "device num: {0}".format(p_in.get_device_count())
for i in range(p_in.get_device_count()):
print p_in.get_device_info_by_index(i)
$ python pyaudio_print_devices.py
device num: 2
{'defaultSampleRate': 44100.0, 'defaultLowOutputLatency': 0.01, 'defaultLowInputLatency': 0.00199546485260771, 'maxInputChannels': 2L, 'structVersion': 2L, 'hostApi': 0L, 'index': 0, 'defaultHighOutputLatency': 0.1, 'maxOutputChannels': 0L, 'name': u'Built-in Microph', 'defaultHighInputLatency': 0.012154195011337868}
{'defaultSampleRate': 44100.0, 'defaultLowOutputLatency': 0.004693877551020408, 'defaultLowInputLatency': 0.01, 'maxInputChannels': 0L, 'structVersion': 2L, 'hostApi': 0L, 'index': 1, 'defaultHighOutputLatency': 0.014852607709750568, 'maxOutputChannels': 2L, 'name': u'Built-in Output', 'defaultHighInputLatency': 0.1}
If you look at "maxInputChannels", you can see that the first device is 2L and the "name" is u'Built-in Microph', so this is the input device.
Next is a script that saves the microphone input to a wav file. PyAudio has a non-blocking processing method that uses callbacks and a blocking processing method that does not use callbacks. Here, the former method that uses callbacks is used for processing. In the callback method, the input signal is converted from short to a float of -1.0 to 1.0, and it is simply combined with the global variable xs.
#!/usr/bin/env python
# vim:fileencoding=utf-8
import time
import numpy as np
import soundfile as sf
import pyaudio as pa
# global
xs = np.array([])
def callback(in_data, frame_count, time_info, status):
global xs
in_float = np.frombuffer(in_data, dtype=np.int16).astype(np.float)
in_float[in_float > 0.0] /= float(2**15 - 1)
in_float[in_float <= 0.0] /= float(2**15)
xs = np.r_[xs, in_float]
return (in_data, pa.paContinue)
if __name__ == "__main__":
# pyaudio
p_in = pa.PyAudio()
py_format = p_in.get_format_from_width(2)
fs = 16000
channels = 1
chunk = 1024
use_device_index = 0
#Create input stream
in_stream = p_in.open(format=py_format,
channels=channels,
rate=fs,
input=True,
frames_per_buffer=chunk,
input_device_index=use_device_index,
stream_callback=callback)
in_stream.start_stream()
# input loop
#Enter something and finish
while in_stream.is_active():
c = raw_input()
if c:
break
time.sleep(0.1)
else:
in_stream.stop_stream()
in_stream.close()
#Save input signal
sf.write("./pyaudio_output.wav", xs, fs)
p_in.terminate()
Do this and type something to break out of the while loop and save the xs in "./pyaudio_output.wav". If you set output = True instead of input = True when opening p_in, it will be treated as a playback device. For more information, see the sample at the bottom of the PyAudio page (https://people.csail.mit.edu/hubert/pyaudio/).
I want to display the frequency response
There is a method in scipy.signal that asks for the frequency response freqz. As I wrote in Article, the part where the polynomial is calculated by np.polyval is heavy, and when it is executed continuously, the slowness is slow. It really stands out. Therefore, as I wrote in the previous article, you can find the frequency response by defining the following method that uses scipy.fftpack.
def my_freqz(b, a=[1], worN=None):
import scipy.fftpack as fft
lastpoint = np.pi
N = 512 if worN is None else worN
w = np.linspace(0.0, lastpoint, N, endpoint=False)
h = fft.fft(b, 2 * N)[:N+1] / fft.fft(a, 2 * N)[:N+1]
return w, h
For example, suppose you want the response of a simple emphasis filter b = [1.0, -0.97] and a de-emphasis filter b = [1.0], a = [1.0, -0.97] that restores its characteristics. You can plot each frequency response with a script like the one below. Note that the range of w is 0 to π, so the horizontal axis when plotting is 0 to FS / 2.
#!/usr/bin/env python
# vim:fileencoding=utf-8
import numpy as np
import matplotlib.pyplot as plt
def my_freqz(b, a=[1], worN=None):
import scipy.fftpack as fft
lastpoint = np.pi
N = 512 if worN is None else worN
w = np.linspace(0.0, lastpoint, N, endpoint=False)
h = fft.fft(b, 2 * N)[:N] / fft.fft(a, 2 * N)[:N]
return w, h
if __name__ == "__main__":
plt.close("all")
N = 1024
FS = 16000.0
EMP = -0.97
b_emp = [1.0, EMP]
a_emp = [1.0]
b_deemp = [1.0]
a_deemp = [1.0, EMP]
(w_emp, h_emp) = my_freqz(b_emp, a_emp, worN=N)
(w_deemp, h_deemp) = my_freqz(b_deemp, a_deemp, worN=N)
fig = plt.figure(1)
ax = fig.add_subplot(2, 1, 1)
ax.semilogx(w_emp * (FS / 2.0) / np.pi,
20.0 * np.log10(np.abs(h_emp)))
ax.grid()
ax.set_xlabel("frequency response [Hz]")
ax.set_ylabel("power [dB]")
ax = fig.add_subplot(2, 1, 2)
ax.semilogx(w_deemp * (FS / 2.0) / np.pi,
20.0 * np.log10(np.abs(h_deemp)))
ax.grid()
ax.set_xlabel("frequency response [Hz]")
ax.set_ylabel("power [dB]")
plt.show()
This will plot a response similar to the one below.

I want to design a digital filter
Various filter design functions are provided in scipy.signal, including FIR filter design functions (firwin, firwin2, remez, etc.) and matlab-compatible IIR design functions (butter, buttord, cheby1, cheb1ord, etc.). ..
For example, to find LPF, BPF, HPF using firwin, you can use the following script.
#!/usr/bin/env python
# vim:fileencoding=utf-8
import numpy as np
import matplotlib.pyplot as plt
import scipy.signal as sg
def my_freqz(b, a=[1], worN=None):
import scipy.fftpack as fft
lastpoint = np.pi
N = 512 if worN is None else worN
w = np.linspace(0.0, lastpoint, N, endpoint=False)
h = fft.fft(b, 2 * N)[:N] / fft.fft(a, 2 * N)[:N]
return w, h
if __name__ == '__main__':
plt.close("all")
fs = 48000.0
num_tap = 1024
lpf_cutoff_hz = 400.0
hpf_cutoff_hz = 1000.0
lpf_cutoff = lpf_cutoff_hz / (fs/2.0)
bpf_band = np.array([lpf_cutoff_hz, hpf_cutoff_hz]) / (fs/2.0)
hpf_cutoff = hpf_cutoff_hz / (fs/2.0)
win = "hann"
lpf = sg.firwin(num_tap, lpf_cutoff, window=win)
bpf = sg.firwin(num_tap, bpf_band, pass_zero=False, window=win)
hpf = sg.firwin(num_tap, [hpf_cutoff, 0.9999], pass_zero=False, window=win)
# plot filter response
w, lpf_h = my_freqz(lpf, worN=num_tap)
w, bpf_h = my_freqz(bpf, worN=num_tap)
w, hpf_h = my_freqz(hpf, worN=num_tap)
lpf_amp = np.abs(lpf_h)
bpf_amp = np.abs(bpf_h)
hpf_amp = np.abs(hpf_h)
fig = plt.figure(1)
ax = fig.add_subplot(111)
ax.semilogx(fs * w/(2 * np.pi), 20.0*np.log10(lpf_amp), "bx-")
ax.semilogx(fs * w/(2 * np.pi), 20.0*np.log10(bpf_amp), "yx-")
ax.semilogx(fs * w/(2 * np.pi), 20.0*np.log10(hpf_amp), "rx-")
ax.set_xlim([0.0, 24000.0])
ax.set_ylim([-150.0, 10.0])
ax.set_ylabel("power [dB]")
ax.set_xlabel("frequency [Hz]")
ax.grid()
ax.legend(["lpf", "bpf", "hpf"], loc="best")
plt.show()
As a result, the graph below is plotted.
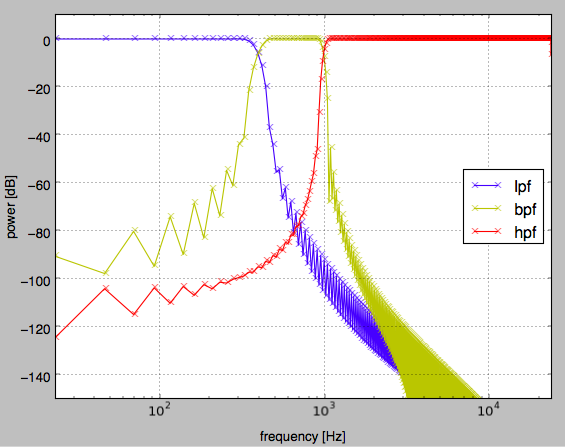
Also, if you want to design a biquad type (secondary IIR) filter, you can create your own function according to EQ Cookbook. For example, in the case of peaking EQ, it looks like the following (return values are b, a).
def peaking_eq(q, gain, f, fs):
A = 10 ** (gain / 40.0)
w0 = 2.0 * np.pi * f / fs
alpha = np.sin(w0) / (2.0 * q)
b = [(1.0 + alpha * A), (-2.0 * np.cos(w0)), (1.0 - alpha * A)]
a = [(1.0 + alpha / A), (-2.0 * np.cos(w0)), (1.0 - alpha / A)]
return (np.array(b) / a[0]), (np.array(a) / a[0])
I want to convert zeros, poles and coefficient arrays b, a
tf2zpk and zpk2tf /doc/scipy/reference/generated/scipy.signal.zpk2tf.html#scipy.signal.zpk2tf) is used. tf stands for time filter and zpk stands for zero, pole, k (gain). When a 6th IIR filter is made and mounted in C as it is, it may diverge due to an error, so if the zero and pole are known, it is possible to decompose the filter into 3 stages of 2nd IIR filters. ..
I want to apply a digital filter to a time series signal
There are two main ways to apply the designed digital filter to a time series signal. The method using time domain convolution is [scipy.signal.lfilter](https://docs.scipy.org/doc/scipy-0.16.0/reference/generated/scipy.signal.lfilter.html#scipy.signal] [scipy.signal.fftconvolve](https://docs.scipy.org/doc/scipy-0.16.0/reference/generated] to process the convolution of the filter as an instant process in the frequency domain. /scipy.signal.fftconvolve.html#scipy.signal.fftconvolve) is used. Below is a script that plots the result of applying lpf as input using each method.
#!/usr/bin/env python
# vim:fileencoding=utf-8
import sys
import scipy.signal as sg
import matplotlib.pyplot as plt
import soundfile as sf
if __name__ == '__main__':
plt.close("all")
#wav file reading
filename = sys.argv[1]
wav, fs = sf.read(filename)
#In the case of stereo 2ch, it is divided into Lch and Rch
wav_l = wav[:, 0]
wav_r = wav[:, 1]
#Monaural input
xs = (0.5 * wav_l) + (0.5 * wav_r)
#LPF design
num_tap = 1024
lpf_cutoff_hz = 400.0
lpf_cutoff = lpf_cutoff_hz / (fs/2.0)
win = "hann"
lpf = sg.firwin(num_tap, lpf_cutoff, window=win)
#Apply linear filter
ys = sg.lfilter(lpf, [1.0], xs)
#Frequency domain filter application
zs = sg.fftconvolve(xs, lpf, mode="same")
#10 seconds plot from the beginning
fig = plt.figure(1)
ax = fig.add_subplot(311)
ax.plot(xs[:fs*10])
ax.set_title("input signal")
ax.set_xlabel("time [pt]")
ax.set_ylabel("amplitude")
ax = fig.add_subplot(312)
ax.plot(ys[:fs*10])
ax.set_title("lfilter output signal")
ax.set_xlabel("time [pt]")
ax.set_ylabel("amplitude")
ax = fig.add_subplot(313)
ax.plot(ys[:fs*10])
ax.set_title("fftconvolve output signal")
ax.set_xlabel("time [pt]")
ax.set_ylabel("amplitude")
fig.set_tight_layout(True)
plt.show()

I want to calculate the group delay
When looking at the characteristics of an all-pass filter, which is a filter that changes only the phase without changing the amplitude, in particular, by finding the [group delay](https://ja.wikipedia.org/wiki/group delay and phase delay), each frequency You can see how much the sample unit delay is. However, scipy.signal does not have the grpdelay function that exists in matlab, so you need to implement grpdelay by yourself in an appropriate way. Therefore, here we will introduce a method for finding the derivative of each frequency by approximation based on the first-order difference.
def grpdelay(w, h, fs):
"""Calculation of group delay characteristics by simple first-order approximation(Results are sample units).. Since it is calculated by the difference, the dimension is reduced by one, so the last element is always set to 0. w is the normalized frequency and h is the frequency characteristic corresponding to w"""
return -1.0 * np.r_[np.diff(np.unwrap(np.angle(h))) / np.diff(w), [0]]
It's not exactly the algorithm used in matlab's grpdelay, but it's enough if you just want to see the rough results.
I want to calculate the time correlation (cross-correlation function)
There is no xcorr in scipy.signal as it is called in matlab. Since xcorr finds the cross spectrum in the frequency domain based on the Wiener-Khinchin theorem and finds the cross-correlation function by inverse transformation, the cross-correlation function can be found faster than the product-sum calculation in the time domain.
The following defines the xcorr method corresponding to the my_correlate method that finds the cross-correlation function in the time domain. ceil2 is a method that looks for a value of a power of 2 that is the same as or greater than the argument. The argument is converted to a character string in binary notation, the value other than the most significant bit is set to 0 in the character string processing, and the value obtained by shifting the number to the left by 1 bit is obtained.
def my_correlate(sig, ref, lag=None):
lag = np.alen(ref) / 2 if lag is None else lag
corrs = []
sig_len = np.alen(sig)
sig_norm = np.sqrt(np.dot(sig, sig))
ref_norm = np.sqrt(np.dot(ref, ref))
sig_expand = np.r_[np.zeros(lag), sig, np.zeros(lag)]
center = lag
for begin in range(center - lag, center + lag + 1):
sig_cut = sig_expand[begin :begin + sig_len]
corrs.append(np.dot(sig_cut, ref))
return np.array(corrs) / (sig_norm * ref_norm)
def ceil2(x):
new_x = 0
if (x & (x - 1)) == 0:
new_x = x
else:
bit_str = bin(x)
head_bit = bit_str[2]
tail_bits = bit_str[3:].replace("1", "0")
new_bit_str = "0b" + head_bit + tail_bits
new_x = int(new_bit_str, 2) << 1
return new_x
def xcorr(sig, ref, lag=None):
import scipy.fftpack as fft
lag = 1024 if lag is None else lag
sig_len = np.alen(sig)
nfft = ceil2(sig_len)
sig_norm = np.sqrt(np.dot(sig, sig))
ref_norm = np.sqrt(np.dot(ref, ref))
sig_ = sig / sig_norm
ref_ = ref / ref_norm
X = fft.fft(sig_, nfft)
Y = fft.fft(ref_, nfft)
# ifft to calculate correlation
corr_p = np.real(fft.ifft(X * np.conjugate(Y), nfft))
corr_m = np.real(fft.ifft(Y * np.conjugate(X), nfft))
# concat
corr = np.r_[corr_m[1:lag+1][::-1], corr_p[:lag+1]]
return corr
Actually, when using FFT, we have to consider the influence of patrol, so I feel that there is room for improvement in the above. Reference: http://www.ikko.k.hosei.ac.jp/~matlab/xcorr.pdf
I want to detect the peak
scipy.signal also has a method called find_peaks_cwt, but it's more convenient. I wanted a light function, so I use the following method.
def find_peaks(a, amp_thre, local_width=1, min_peak_distance=1):
"""
The peak is detected from the array by giving the threshold value, the window width for determining the maximum / minimum, and the minimum distance between peaks.
Internally, the distance between peaks is calculated by distinguishing between positive and negative peaks, so close positive and negative peaks are detected.
:rtype (int, float)
:return tuple (ndarray of peak indices, ndarray of peak value)
"""
# generate candidate indices to limit by threthold
idxs = np.where(np.abs(a) > amp_thre)[0]
# extend array to decide local maxima/minimum
idxs_with_offset = idxs + local_width
a_extend = np.r_[[a[0]] * local_width, a, [a[-1]] * local_width]
last_pos_peak_idx = 0
last_neg_peak_idx = 0
result_idxs = []
for i in idxs_with_offset:
is_local_maximum = (a_extend[i] >= 0 and
a_extend[i] >= np.max(a_extend[i - local_width: i + local_width + 1]))
is_local_minimum = (a_extend[i] < 0 and
a_extend[i] <= np.min(a_extend[i - local_width: i + local_width + 1]))
if (is_local_maximum or is_local_minimum):
if is_local_minimum:
if i - last_pos_peak_idx > min_peak_distance:
result_idxs.append(i)
last_pos_peak_idx = i
else:
if i - last_neg_peak_idx > min_peak_distance:
result_idxs.append(i)
last_neg_peak_idx = i
result_idxs = np.array(result_idxs) - local_width
return (result_idxs, a[result_idxs])
that's all
I feel like I have something else to write, but that's it. Next time is @kimihiro_n.
Recommended Posts