Introduction to algorithms with java --Search (depth-first search)

Article summary

This is a series of articles that I have compiled in my study and memo. This is a continuation of this article. Introduction to Algorithms with java-Search (Full Search, Binary Search) In this article

--Depth-first search

I will study about. I wrote it in the continuation of the previous article.

Depth-first search

It's like this from here, but let's proceed. While learning and summarizing. Depth-first search. It seems that it is also called DFS (depth-first-search). By the way, I often see this word. Depth-first search and breadth-first search seem to be useful for searching trees and graphs. I will omit the explanation of trees and graphs. The figure is shown below. (From wikipedia) It's like DFS to search trees in this order with priority on depth.

For those who say, "I don't know what is depth-first!", I think it's one shot if you look at the search order of breadth-first search.

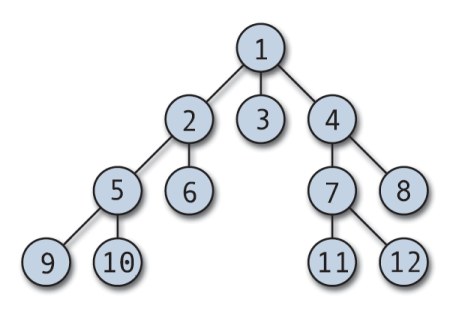
Did you see the difference in numbers? Depth-first search searches in a straight line from the root to a node that has no children, and breadth-first search searches for nodes with a depth of 1 from the root in order.

By the way, there are two types of implementation methods.

--How to use stack (last in, first out data structure) --How to use a recursive function

... I feel like I'm afraid because it's crazy. You can't understand without seeing an example. If you look for a simple example, you can't find an example that you can intuitively understand. .. As shown in the figure above, it's just a way to search in that order! Is it like that? I will understand it while looking at problem examples and solving them. If you can understand it, maybe you can make a simple example?

Example: AtCoder --arc031-b "Landfill"

\(A1,1\)\(A1,2\)...\(A1,10\)
\(A2,1\)\(A2,2\)...\(A2,10\)
:
\(A10,1\)\(A10,2\)...\(A10,10\)

I've been studying by looking at other people's sources and various blogs. The policy is as follows. Maybe many people did this.

――Search for one square in 10 * 10 lands, "If you reclaim this one square, you can make the whole into one island." -Count the number of squares on the island by depth-first search from the first selected square. If the number of squares searched at this time is the square of the island received in the first input + 1 square (if the sea is reclaimed), the condition is met.

[Answer example]

main.java

import java.util.Scanner;

public class Main {

	//Map of the island
	static char[][] islandMap;

	public static void main(String[] args) {

		Scanner sc = new Scanner(System.in);

		//Map of the island
		islandMap = new char[10][10];

		//Number of trout on the island
		int countIsland = 0;

		//Final output
		String ans = "NO";

		//Receive input and complete the map of the island, count the number of island squares
		for (int i = 0; i < 10; i++) {
			islandMap[i] = sc.next().toCharArray();
			for (int j = 0; j < 10; j++) {
				if (islandMap[i][j] == 'o') {
					countIsland++;
				}
			}
		}

		//Search for squares from the upper left square with a double loop
		for (int i = 0; i < 10; i++) {
			for (int j = 0; j < 10; j++) {

				//Island count temporary variable
				int countIslandInLoop = countIsland;

				//In the case of the sea, make it land. Also increase the number of islands by one
				if (islandMap[i][j] == 'x') {
					islandMap[i][j] = 'o';
					countIslandInLoop = countIsland + 1;
				}

				/*
				 *Depth-first search is performed.
				 *dfsCountIsland ・ ・ ・ The number of land-based islands counted by dfs
				 *checked ・ ・ ・ Judgment whether the square has been searched by dfs
				 */
				dfsIslandCount = 0;
				boolean[][] checked = new boolean[10][10];

				dfs(i, j, checked);

				if (dfsIslandCount == countIslandInLoop) {
					ans = "YES";
					break;
				}

				//Put back the landfilled square and go to the next loop
				if (countIslandInLoop == countIsland + 1) {
					islandMap[i][j] = 'x';
				}
			}
			if ("YES".equals(ans)) {
				break;
			}
		}

		System.out.println(ans);

	}

	//Number of squares on land-based islands currently counted by dfs
	static int dfsIslandCount;

	//Depth-first search
	static void dfs(int i, int j, boolean[][] checked) {
		//If it is beyond the square, has been searched, or is the sea, change direction.
		if (i < 0 || i > 9 || j < 0 || j > 9 || checked[i][j] || islandMap[i][j] == 'x') {
			return;
		}

		//If the square you are searching for is land, increment the land count.
		if (islandMap[i][j] == 'o') {
			dfsIslandCount++;
		}

		//Make the current square searched
		checked[i][j] = true;

		//Search up, down, left and right squares
		dfs(i + 1, j, checked);
		dfs(i - 1, j, checked);
		dfs(i, j + 1, checked);
		dfs(i, j - 1, checked);

		return;

	}
}

No, it was really difficult. It's very difficult to put it in a global variable or how to recurse a search.

It doesn't matter, but AtCoder has prepared an example of such an algorithm. AtCoder --atc001-a "Depth-first search"

For the time being, I've used it as the code for this problem, so let's look at the dfs part from above.

I wonder if I can see about 2 squares. First, the example input is as follows:

xxxxxxxxxx
xoooooooxx
xxoooooxxx
xxxoooxxxx
xxxxoxxxxx
xxxxxxxxxx
xxxxoxxxxx
xxxoooxxxx
xxoooooxxx
xxxxxxxxxx

• × is the sea and ○ is the island. The map at this time looks like the following. (Well, you can tell from the character string.)

Let's think about DFS for cell (1) and DFS for cell (2).

In the dfs method of the above code for clarity, The if statement of the first process is "// If it exceeds the square, has been searched, or if it is the sea, change direction." The second process is "// If the cell you are searching for is land, the land count is incremented", The process of No. 3 is "// Make the current square searched", The 4th process is the process of "// Search for squares on the top, bottom, left, and right". (I will explain which one is called each time.)

DFS in case of ①

Let's follow the source. I will mainly explain about moving squares with dfs.

Here is the figure in which the square of ① was reclaimed in the second process.

I also added the values of i and j. Then it's DFS. After making the current cell searched by the 3rd process, proceed to the 4th process. The first thing to be called dfs(i + 1, j, checked); is. i = 0, j = 0 dfs(1, 0, checked); is not it. With this, I moved to the square of i = 1, j = 0, but since the destination is the sea, I get caught in the if statement in the first process. It will be returned.

Next, proceed to the second line of the 4th process. dfs(i - 1, j, checked); Specifically dfs(-1, 0, checked); is not it. It moves to the square of i = -1, j = 0 (outside the map) and is returned in the first process.

The same is true for the 3rd and 4th lines. This completes the search for cell ①. It's hard to understand because it's not recursive yet. However, I think it would be good to think from such an easy-to-understand example.

DFS in case of ②

Here is an example of the answer. Let's be enthusiastic and DFS. Here is a figure of landfill with i and j numbers.

After the first call, the red part is called, the movements are programmatically indented and written in order. It feels like recursion when indented. We will start with the fourth process of the first dfs call. ** Let's go all out! !! ** ** Currently (i, j) = (5,4). The order in which they are called, including recursion, is as follows:

1. dfs(6, 4, checked);
2. dfs(7, 4, checked);
3. dfs(8, 4, checked);
4. dfs (9, 4, checked); ← Because it is the sea, it ends
5. dfs (7, 4, checked); ← Ended because it was searched on the 02nd line
6. dfs(8, 5, checked);
7. dfs (9, 5, checked); ← Because it is the sea, it ends
8. dfs(7, 5, checked);
9. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
10. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
11. ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥
12. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
13. dfs(8, 6, checked);
14. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
15. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
16. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
17. ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥
18. ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥
19. dfs(8, 3, checked);
20. dfs (9, 3, checked); ← Because it is the sea, it ends
21. dfs(7, 3, checked);
22. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
23. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
24. ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥
25. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
26. dfs(8, 2, checked);
27. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
28. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
29. ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥
30. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
31. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
32. dfs (6, 4, checked); ← Ended because it was searched on the 01st line
33. dfs (7, 5, checked); ← Ended because it was searched on the 08th line
34. dfs (7, 3, checked); ← Ended because it was searched on the 21st line
35. dfs (5, 4, checked); ← End because it has been searched first
36. dfs (6, 5, checked); ← Because it is the sea, it ends
37. dfs (6, 3, checked); ← Because it is the sea, it ends
38. dfs(4, 4, checked);
39. dfs (5, 4, checked); ← End because it has been searched first
40. dfs(3, 4, checked);
41. dfs (4, 4, checked); ← Ended because it was searched on the 38th line
42. dfs(2, 4, checked);
43. dfs (3, 4, checked); ← Ended because it was searched on the 40th line
44. dfs(1, 4, checked);
45. ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥
46. dfs (0, 4, checked); ← Because it is the sea, it ends
47. dfs(1, 5, checked);
48. dfs(2, 5, checked);
49. dfs(3, 5, checked);
50. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
51. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
52. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
53. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
54. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
55. dfs(2, 6, checked);
56. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
57. dfs(1, 6, checked);
58. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
59. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
60. dfs(1, 7, checked);
61. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
62. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
63. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
64. ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥
65. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
66. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
67. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
68. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
69. dfs (0, 5, checked); ← Because it is the sea, it ends
70. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
71. ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥
72. dfs(1, 3, checked);
73. dfs(2, 3, checked);
74. dfs(3, 3, checked);
75. ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥
76. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
77. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
78. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
79. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
80. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
81. dfs(2, 2, checked);
82. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
83. dfs(1, 2, checked);
84. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
85. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
86. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
87. dfs(1, 1, checked);
88. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
89. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
90. ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥
91. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
92. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
93. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
94. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
95. ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
96. Ended because it has been searched on the 84th line dfs (1, 2, checked); ← 84th line
97. dfs (2, 5, checked); ← Ended because it was searched on the 42nd line
98. dfs (2, 3, checked); ← Ended because it was searched on the 74th line
99. dfs (3, 5, checked); ← Ended because it was searched on the 50th line
100. dfs (3, 3, checked); ← Ended because it was searched on the 75th line
101. dfs (4, 5, checked); ← Because it's the sea, it's over
102. dfs (4, 3, checked); ← Because it's the sea, it's over
103. dfs (5, 5, checked); ← Because it's the sea, it's over
104. dfs (5, 3, checked); ← Because it's the sea, it's over

** Oh ... it's over ... ** I'm super tired. It wasn't something that people would do by hand. Well, I did it so much, so let's check what kind of movement was being searched for. I tried to express the search order in white letters.

You can see it by looking at the figure, and you can see it by looking at the feeling of loop, but DFS is like "If you can't get to the point, you'll change direction."

I also think that the word "stack" came out, but it feels like this recursion method is exactly the order of the first-in, second-out stacks. Even if you don't use a data structure called a stack, you can see that if you write an implementation recursively, it will be a stack-like process.

Did you understand depth-first search? I could understand a little. (Oh, I'm tired ...)

It's been a long time, so I'll explain breadth-first search again next time. Next time we look forward to! !!