Machine learning (TensorFlow) + Lotto 6

It is a play to try to predict even the number of Lotto 6 using deep learning. Of course, the lottery only gives random numbers every time, so it shouldn't work, but it seems that some people are seriously expecting it, and I wrote the code quickly, so rather than burying it in the HDD. I will publish it. I'm not doing it very seriously, so the explanation is also appropriate. Please comment if you have any concerns.

Target

--Lotto 6 winning number prediction.

• I chose Lotto 6 because it is the only number-based lottery I have bought.

Overview

I was wondering what to enter, but I chose the winning numbers for the past 5 times. Lotto 6 is a mechanism in which 6 are selected from 43 numbers, and if all 6 are won, the first prize is awarded. So, the output is 43 flags, for example, if 1,3,4,11,20,43 is the winning number, [1,0,1,1,0,0, ..... 0, I assumed to expect a flag like 0,1]. (Strictly speaking, it is a little different because it passes through Softmax) The data was scraped from Mizuho Bank's website. It will be about 1000 data.

environment

TensorFlow 0.7 Ubuntu 14.04 AWS EC2 microinstance

Implementation

Only the parts that are likely to be points are excerpted.

There are two hidden layers and the number of units is 1000 and 500, respectively. The output is 43.

def inference(x_ph, keep_prob):

    with tf.name_scope('hidden1'):
        weights = tf.Variable(tf.truncated_normal([data_num * NUM_CLASSES, NUM_HIDDEN1], stddev=stddev), name='weights')
        biases = tf.Variable(tf.zeros([NUM_HIDDEN1]), name='biases')
        hidden1 = tf.nn.relu(tf.matmul(x_ph, weights) + biases)

    with tf.name_scope('hidden2'):
        weights = tf.Variable(tf.truncated_normal([NUM_HIDDEN1, NUM_HIDDEN2], stddev=stddev), name='weights')
        biases = tf.Variable(tf.zeros([NUM_HIDDEN2]), name='biases')
        hidden2 = tf.nn.relu(tf.matmul(hidden1, weights) + biases)

    # DropOut
    dropout = tf.nn.dropout(hidden2, keep_prob)

    with tf.name_scope('softmax'):
        weights = tf.Variable(tf.truncated_normal([NUM_HIDDEN2, NUM_CLASSES], stddev=stddev), name='weights')
        biases = tf.Variable(tf.zeros([NUM_CLASSES]), name='biases')
        y = tf.nn.softmax(tf.matmul(dropout, weights) + biases)

    return y

Loss calculation part. The label (target) of the correct answer is a flag of 0 or 1, but since y comes through softmax, it is a haze that adds up to 1 as a whole, and since the scale does not match as it is, target also passes through softmax. ..

def loss(y, target):

    softmax_target = tf.nn.softmax(target)
    cross_entropy = tf.nn.softmax_cross_entropy_with_logits(y, softmax_target, name='xentropy')
    loss = tf.reduce_mean(cross_entropy, name='xentropy_mean')

    return loss

Training.

def training(sess, train_step, loss, x_train_array, y_train_array):

    summary_op = tf.merge_all_summaries()

    init = tf.initialize_all_variables()
    sess.run(init)

    summary_writer = tf.train.SummaryWriter(LOG_DIR, graph_def=sess.graph_def)

    for i in range(int(len(x_train_array) / bach_size)):
        batch_xs = getBachArray(x_train_array, i * bach_size, bach_size)
        batch_ys = getBachArray(y_train_array, i * bach_size, bach_size)
        sess.run(train_step, feed_dict={x_ph: batch_xs, y_ph: batch_ys, keep_prob: 0.8})
        ce = sess.run(loss, feed_dict={x_ph: batch_xs, y_ph: batch_ys, keep_prob: 1.0})

        summary_str = sess.run(summary_op, feed_dict={x_ph: batch_xs, y_ph: batch_ys, keep_prob: 1.0})
        summary_writer.add_summary(summary_str, i)

result

loss 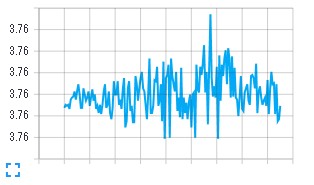You can see that it hasn't become a mess (laughs) I learned that it would be like this if I couldn't help it.

Forecast

I know it's totally useless, but let's actually predict it. Let's predict the 1046th using the data of the 1045th to 1041st. The input looks like the following,

[[01,19,21,30,31,43],[03,07,16,26,34,39],[21,29,30,32,38,42],[04,10,11,12,18,25],[14,22,27,29,33,37]]

The result is below.

[6, 10, 12, 23, 27, 38]

The actual winning numbers are [06, 13, 17, 18, 27, 43]. I'm hitting two. By the way, it costs 1,000 yen to hit three. I'm not sure how many hits are the average (I don't know how to calculate), but let's throw away the weird expectations.