Use combinatorial optimization
Introduction
I will explain the know-how for using combinatorial optimization.
The trick to using combinatorial optimization is to understand the big picture. By knowing what the elements are and how they relate to each other, you will be able to approach the problem you want to solve. You can easily make various optimizations by using Python. Let's check it later while looking at the actual code. First, let's look at some familiar optimization examples.
Let's think
The other day, when you returned home, you were told to bring vegetables as a souvenir. The vegetables in Tokyo are expensive, so I was delighted that they were "profitable", but the amount was too large. Suppose you can only bring back 5 kg at most. (Please do not use the courier service.) Also, vegetables will be damaged if cut, so I will take them home as they are.
You thought, "Let's choose from the ones with the highest selling price per kg." In fact, this is not the best method (although the greedy algorithm, a fast and good approximation). How do you know the really best way?
If you look at all the possibilities, you'll know how to optimize. However, all vegetable combinations will explode as the number of vegetables increases and cannot be calculated. ** Mathematical optimization ** can be used to solve such problems. Mathematical optimization uses mathematical formulas to represent the problem with a ** mathematical model **. The previous example is
| Maximize | $ \ sum_i {p_i x_i} $ | $ p_i $: Selling Price |
| $ \ sum_i {w_i x_i} \ le 5 $ | $ w_i $: Weight | |
| $ \ forall x_i \ in \ {0, 1 \} $ | $ x_i $: Whether to bring it home > |
| Continuous optimization: | Continuous elements only |
| Combinatorial optimization: | Includes non-continuous discrete elements |
Formulation
Lesson 1
** Combinatorial optimization formulates a mathematical model. ** **
To formulate, we need to determine three factors.
| 1. What do you want to decide? | "I want to decide which vegetables to bring back" |
| 2. What would you like to do? | "I'm glad if the total selling price of the vegetables I bring home is high." |
| 3. What do I have to protect? | "Weigh less than 5 kg of vegetables to bring back" |
| 1. Variables: | $ \ forall x_i \ in \ {0, 1 \} $ | |
| 2. Objective function: | $ \ sum_i {p_i x_i} $ | $ \ rightarrow $ maximum |
| 3. Constraints: | $ \ sum_i {w_i x_i} \ le 5 $ |
It takes some getting used to to be able to formulate. This time, we'll look at some examples later. If you want to study in detail, please refer to the book "Combinatorial optimization that can be used from today". To find the best answer from a mathematical model, use a tool (made by a wise man). This tool is called an optimized solver, or ** solver ** for short. In other words, you can simply represent the problem (so that anyone can understand it) and use the solver to come up with a solution (the answer). These days, this solver is easy to use and its performance has improved a lot. Everyone is starting to try optimizations.
Typical problem
What other examples are there besides the previous ones? You may have searched for a transfer station on the web when you returned home.
I want to find the shortest (or cheapest) route from the station closest to your home to the station closest to your parents' home.
This is also an optimization problem. There are many optimization problems in many places. However, it is difficult to formulate each problem. In fact, different problems often have the same formulation. That way, you don't have to bother to formulate it, which is convenient. We will call the common problems in the world ** typical problems **.
Lesson 2
** Understand typical problems. ** **
Collect related typical problems and create a framework called ** typical problem class **. There are seven typical problem classes. We have carefully selected the most commonly used questions.
| Typical problem class | Typical problem |
| Graph network problem | Minimum spanning tree problem |
| Maximum stable set problem | |
| Maximum cut problem | |
| Vertex cover problem | |
| Shortest path problem | |
| Maximum flow problem | |
| Minimum cost flow problem | |
| Route problem | Transport route problem |
| Traveling salesman problem | |
| Set cover / partition problem | Set cover problem |
| Partition of a set problem | |
| Scheduling problem | Job shop problem |
| Work Scheduling Problem | |
| Cutout / jamming problem | Knapsack problem |
| Bin packing problem | |
| n-dimensional packing problem | |
| Placement problem | Facility placement problem |
| No capacity constraint Facility placement problem | |
| Assignment / matching problem | Secondary allocation problem |
| Generalized allocation problem | |
| Maximum matching problem | |
| Weight matching problem | |
| Stable matching problem |
How to choose vegetables is called ** knapsack problem **, and searching for transfer stations is called ** shortest path problem **. Typical problems are well-studied and often have efficient solutions. Alternatively, it is formulated so that it can be solved immediately. Let's do it later. See Typical Problems and Execution Methods for examples of executing all the typical problems listed here.
General problem
I'm going to talk about the container work I'm doing lately. It is thanks to container transportation that people all over the world can buy various things cheaply. This is because products produced in China can be shipped to Japan, the United States, and Europe in large quantities at low prices. However, empty containers are piled up more and more. I have to go back to China again. Determining when, where, and where to return is the ** minimum cost flow problem **. However, there are some constraints that cannot be expressed by the minimum cost flow problem. One is called cabotage. Cabotage is to regulate domestic transportation only to domestic companies. If the typical problem cannot be dealt with, the mathematical model is treated as it is. The problem represented by the mathematical model is called a ** general problem **. Typical problems can also be viewed as general-purpose problems. General-purpose problems have a more general classification than typical problems.
Lesson 3
** Understand generic problems. ** **
What are the general problems?
Differences in general-purpose problems are due to differences in variables, objective functions, and constraints. Different general-purpose problems have different solutions (algorithms). The ease of solving is completely different depending on the type of this solution. Also, the solver may be different for each generic problem. As much as possible, it is important to be able to take it to a general-purpose problem that can be easily solved. The general problem is a parent-child relationship.

All optimization problems are non-linear optimization problems. Why bother with non-linear optimization? That's because it's inefficient to treat a linear optimization problem as a non-linear optimization. The term nonlinear optimization implicitly suggests that there is a nonlinear objective function or a nonlinear constraint.
** Linear optimization problem **
The easiest general-purpose problem to solve is a linear optimization problem. The minimum cost flow problem and the shortest path problem are also linear optimization problems. The problem is that the variable is a continuous variable and the objective function and constraints are represented linearly (linear expression). This has come to be able to solve even fairly large problems.
** Mixed integer optimization problem **
The objective function and constraints are linear, but the problem of including an integer variable (where only integers are allowed) in the variable is called a mixed integer optimization problem. The knapsack problem is also a mixed integer optimization problem. This is a common problem in practice and many of the problems I am dealing with. It's a difficult problem, but recently it has become possible to solve it depending on the formulation and the scale of the problem. "We are now able to solve mixed integer optimization problems." This is the reason why the optimization threshold has been lowered. For beginners of mathematical optimization, one goal will be to formulate a simple mixed integer optimization problem. However, in practice, it is difficult to deal with mixed integer optimization problems, and it may require some ingenuity.
** Non-linear optimization problem **
Non-linear optimization is an even more difficult problem. However, if it is a small scale, it can be solved even at present. Also, among the nonlinear optimizations, the nonlinear convex optimization can be handled even on a large scale, but it is omitted here.
We will see these three examples later.
Relationship between typical problems and general-purpose problems
All mathematical optimization problems are one of the general problems. General-purpose problems can be seen as a major classification of combinatorial optimization problems. However, this classification is too rough. The classification of living things is like vertebrates and invertebrates. A typical problem can be seen as a subclass. In terms of living things, are they reptiles and mammals? It will be easier to remember because you can feel the typical problem more closely.

--One typical problem class may contain different generic problems. ――The formulation can be said to be a blueprint like DNA in living things. However, even though an organism has only one DNA, one problem can be seen as a separate problem. ――The solver (that is, the solution) changes depending on how you think of it as a general-purpose problem or a typical problem. --In general, the typical problem solver is more efficient than the general problem solver.

I will supplement the general problem. Vertebrates and invertebrates in living organisms are separate groups, but are basically inclusive in the classification of general problems. That is, all the problems are nonlinear optimization problems, among which are mixed integer optimization problems, and among them are linear optimization problems. In other words, a linear optimization problem is both a mixed integer optimization problem and a nonlinear optimization problem. The mixed integer optimization problem is also a nonlinear optimization problem. This is also true when applying the solver. That is, the nonlinear optimization solver can handle all nonlinear optimization problems, mixed integer optimization problems, and linear optimization problems. The mixed integer optimization solver cannot handle general nonlinear optimization problems, but can handle mixed integer optimization problems and linear optimization problems. The linear optimization solver can only handle linear optimization problems. By convention, the mixed integer-optimized solver and the linear-optimized solver are often a single solver.
Some non-linear optimization solvers can and cannot consider constraints, but for practitioners, it seems sufficient to care only for solvers that can consider constraints, so here we assume that constraints can be considered. I am.
Solvers perform better in smaller areas. For linear optimization problems, the optimal solution can be obtained faster by using the linear optimization solver. Using a nonlinear optimization solver for a linear optimization problem has disadvantages such as "it is necessary to specify an initial solution" and "it takes a huge amount of calculation time".
There is a much finer classification among optimization researchers, but for many practitioners, three types are sufficient: non-linear optimization, mixed integer optimization, and linear optimization. The mixed integer optimization problem is also called the mixed integer linear optimization problem. Researchers call linear optimization LP (Linear Programming), mixed integer optimization MIP or MILP (Mixed Integer Linear Programming), and nonlinear optimization NLP (Non Linear Programming). Programming was originally translated as "planning", but recently it has come to be called optimization, so we have unified it with optimization here as well. Since optimization is Optimization, the way it is called may change in the future.
Example of executing a typical problem with Python
Lesson 4
** Let's try it. ** **
** Knapsack problem **
Pack some luggage in the knapsack. Maximize the sum of the weights of the packages so that the sum of the sizes of the packages to be packed does not exceed the capacity of the knapsack.
python
from ortoolpy import knapsack
size = [21, 11, 15, 9, 34, 25, 41, 52]
weight = [22, 12, 16, 10, 35, 26, 42, 53]
capacity = 100
knapsack(size, weight, capacity)
>>>
(105, [0, 1, 3, 4, 5])
You will get the sum of the values of the selected packages (105) and the order of the selected packages ([0, 1, 3, 4, 5]).
** Shortest path problem **
In the graph, find the shortest route from the start point to the end point.
python
import networkx as nx
g = nx.fast_gnp_random_graph(8, 0.26, 1)
nx.dijkstra_path(g, 0, 2)
>>>
[0, 1, 6, 3, 5, 2]
Create a random graph of 8 points to get a list of nodes ([0, 1, 6, 3, 5, 2]) that are the shortest paths from node 0 to node 2.
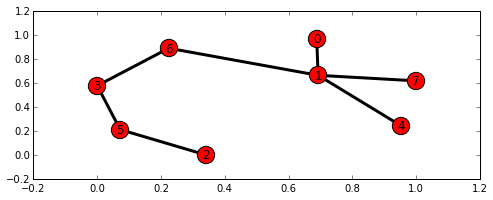
For other typical problem execution examples, see Typical problem and execution method.
Example of executing a general problem using Python
For how to use PuLP, see [How to create a general problem with PuLP](#pulp% E3% 81% A7% E3% 81% AE% E6% 95% B0% E7% 90% 86% E5% 95% 8F% E9 Please refer to% A1% 8C% E3% 81% AE% E4% BD% 9C% E3% 82% 8A% E6% 96% B9).
** Knapsack problem **
Pack some luggage in the knapsack. Maximize the sum of the weights of the packages so that the sum of the sizes of the packages to be packed does not exceed the capacity of the knapsack.
python
from pulp import *
size = [21, 11, 15, 9, 34, 25, 41, 52]
weight = [22, 12, 16, 10, 35, 26, 42, 53]
capacity = 100
r = range(len(size))
m = LpProblem(sense=LpMaximize) #Mathematical model
x = [LpVariable('x%d'%i, cat=LpBinary) for i in r] #variable
m += lpDot(weight, x) #Objective function
m += lpDot(size, x) <= capacity #Constraint
m.solve()
print((value(m.objective), [i for i in r if value(x[i]) > 0.5]))
>>>
(105.0, [0, 1, 3, 4, 5])
The knapsack problem is a mixed integer optimization problem for general problems.
** Shortest path problem **
In the graph, find the shortest route from the start point to the end point.
python
from pulp import *
import networkx as nx
g = nx.fast_gnp_random_graph(8, 0.26, 1).to_directed()
source, sink = 0, 2 #start point,end point
r = list(enumerate(g.edges()))
m = LpProblem() #Mathematical model
x = [LpVariable('x%d'%k, lowBound=0, upBound=1) for k, (i, j) in r] #variable(Whether to enter the road)
m += lpSum(x) #Objective function
for nd in g.nodes():
m += lpSum(x[k] for k, (i, j) in r if i == nd) \
== lpSum(x[k] for k, (i, j) in r if j == nd) + {source:1, sink:-1}.get(nd, 0) #Constraint
m.solve()
print([(i, j) for k, (i, j) in r if value(x[k]) > 0.5])
>>>
[(0, 1), (1, 6), (3, 5), (5, 2), (6, 3)]
The shortest path problem is a linear optimization problem for general-purpose problems. The shortest path problem has an efficient solution called Dijkstra's algorithm. It is not recommended to solve it as a general-purpose problem. Dijkstra's algorithm is [Example of executing a typical problem with Python](# python-% E3% 81% AB% E3% 82% 88% E3% 82% 8B% E6% A8% 99% E6% BA% 96% E5% It is used in the example (nx.dijkstra_path) of 95% 8F% E9% A1% 8C% E3% 81% AE% E5% AE% 9F% E8% A1% 8C% E4% BE% 8B).
** Portfolio optimization problem **
Determine the percentage ($ x_i
) to buy the stock. Minimize the risk (variance ( v_i $)), subject to the lower limit of return on investment (t / yen). However, each issue will be independent.
python
import numpy as np, scipy.optimize as so
p = [31, 86, 29, 73, 46, 39, 58] #Profit/Circle
v = [10, 60, 25, 50, 35, 30, 40] #Distributed/Circle
t = 50 #Target profit/Circle
so.fmin_slsqp(lambda x: sum(v*x*x), np.zeros(len(p)),
eqcons=[lambda x: sum(x) - 1], ieqcons=[lambda x: sum(p*x) - t])
>>>
Optimization terminated successfully. (Exit mode 0)
Current function value: 4.50899167487
Iterations: 14
Function evaluations: 136
Gradient evaluations: 14
array([ 0.26829785, 0.13279566, 0.09965076, 0.1343941 , 0.11783349,
0.11506705, 0.13196109])
The portfolio optimization problem becomes a non-linear optimization problem of general purpose problems.
Graph network
There are many graph network problems in combinatorial optimization problems. It's important, so I'll briefly introduce it here. A graph is a structure consisting of points and edges connecting the points. It is often used to abstractly represent real-life relationships.
$ G = (V, E) $ means that "graph (G) is composed of point set (V) and edge set (E)". A graph with one-way edges is called a directed graph, and a graph with other sides is called an undirected graph. A series of edges from one point to another is called a path. A cycle in which the start and end points of a route are connected is called a cycle. A network is a network that considers the flow of something on the side of the graph. There are road networks, communication networks, etc.
Software installation
We recommend using Anaconda as an easy way to install. To install Anaconda, download the installer from Site and execute it.
Anaconda includes Python itself and many packages for scientific computing. Other than Anaconda, the necessary software is PuLP, which is a modeler of mathematical optimization, and a library for typical problems.
--Install PuLP with "pip install pulp". --Installation of the library for typical problems is "pip install or toolpy".
How to create a general-purpose problem with PuLP
- Import library
- from pulp import * --Creation of mathematical model --For minimization problems: m = LpPrblem () --For maximization problems: m = LpProblem (sense = LpMaximize) --Creating variables --Continuous variable: x = LpVariable (variable name, lowBound = 0) --0-1 Variable: x = LpVariable (variable name, cat = LpBinary) --List of continuous variables: x = [LpVariable (ith variable name, lowBound = 0) for i in range (n)] --Make sure the variable names are different --Setting the objective function --m + = expression --Adding constraints --m + = expression == expression --m + = expression <= expression --m + = expression> = expression --Example of expression
- 2 * x + 3 * y - 5 --Sum: lpSum (list of variables) --Inner product: lpDot (list of coefficients, list of variables) --Run solver
- m.solve() --Values of variables, expressions and objective functions --value (variable), value (expression), value (m.objective)
reference
-Python in optimization -Power of combinatorial optimization solver --Professor Miyashiro's Memo of Integer Programming
Points to note
There are a few things to keep in mind when using optimizations in practice. Current optimization techniques cannot fully model real-world challenges. You can't solve it without simplifying the model by truncating the less important parts.
Therefore, the result of optimization is often not usable as it is. In that case, it is important to verify to see what the problem is. How to show the results is also important to find the problem quickly.
To deepen understanding
Here are some keywords for further study.
--Computational complexity, order notation, class P, class NP --Operations Research, Modeling, Metaheuristics, Duality, Mitigation Problems, Artificial Intelligence, Machine Learning, Game Theory --Related academic societies -Operations Research Society -Japan Society for Industrial and Applied Mathematics --Optimization topics and explanations -Kyoto University Optimization Mathematical Field (Mathematical Optimization Laboratory) -Mathematical model-wikipedia -Modeling and optimization of social systems --Kinmo kyuri zu -Problem Solving and Mathematics-Mathematical Girls -What to be careful about when "understanding" a complex system with a mathematical model --Default Mode
Digression
In living things, the two nomenclature by Linne (for example, Homo sapiens for human beings) is common, but even in optimization, the way of thinking of general-purpose problems and typical problems may be similar to this.
The solver will vary depending on whether you consider it a general-purpose problem or a typical problem, but you must make your own judgment. In the future, it may be possible to determine automatically. In other words, if you give it to the solver as a general-purpose problem, and if you analyze it and find that it is one of the typical problems, you may automatically use a more efficient solution.
Do you know Higashi Robo-kun?
This is a research project led by the National Institute of Informatics, with the theme of "Do robots enter the University of Tokyo?".
In fact, the optimization approach based on typical problems is similar to that of Torobo-kun. It is about solving a wide variety of problems as typological problems. Looking at this attempt, it seems that the day will come when it will be possible to automatically optimize and solve problems simply by writing the problem in Japanese.
But until then, you'll have to think for yourself and move your hands. Also, by doing so, you will gradually learn how to deal with more complex problems.
Recommended Posts