[Reference] [Deep Learning from scratch](https://www.amazon.co.jp/%E3%82%BC%E3%83%AD%E3%81%8B%E3%82%89%E4% BD% 9C% E3% 82% 8BDeep-Learning-% E2% 80% 95Python% E3% 81% A7% E5% AD% A6% E3% 81% B6% E3% 83% 87% E3% 82% A3% E3 % 83% BC% E3% 83% 97% E3% 83% A9% E3% 83% BC% E3% 83% 8B% E3% 83% B3% E3% 82% B0% E3% 81% AE% E7% 90 % 86% E8% AB% 96% E3% 81% A8% E5% AE% 9F% E8% A3% 85-% E6% 96% 8E% E8% 97% A4-% E5% BA% B7% E6% AF % 85 / dp / 4873117585)

What is the activation function?

The activation function is responsible for determining how the sum of the input signals is activated. This serves as an arrangement for the values passed to the next layer.

Typically, In the activation function of "simple perceptron", "step function" etc. are used, In the activation function of "multilayer perceptron (neural network)", "sigmoid function, softmax function" and identity function are used. Also, while these "step function, sigmoid function, softmax function" are called non-linear functions, functions such as "y = cx" are called linear functions. In general, neural networks do not use linear functions. The reason for this is "[Why not use linear functions in Multilayer Perceptron?](Https://qiita.com/namitop/items/d3d5091c7d0ab669195f#%E3%81%AA%E3%81%9C%E5%A4%" 9A% E5% B1% A4% E3% 83% 91% E3% 83% BC% E3% 82% BB% E3% 83% 97% E3% 83% 88% E3% 83% AD% E3% 83% B3% E3% 81% A7% E7% B7% 9A% E5% BD% A2% E9% 96% A2% E6% 95% B0% E3% 82% 92% E4% BD% BF% E3% 82% 8F% E3% 81% AA% E3% 81% 84% E3% 81% AE% E3% 81% 8B) ”. In general, softmax and identity functions are used in the output layer.

Step function

The step function is a function that switches the output at the threshold value. Also called a "step function". A function commonly used in simple perceptrons (single-layer networks).

As an example, a step function that becomes 0 when the entered value is 0 or less and 1 when it is greater than 0 The implementation and operation are shown below.

def step_function(x):
  if x>0:
    return 1
  else:
    return 0

# step_function(4) => 1
# step_function(-3) => 0

The graph can be implemented as follows. step_function is implemented so that it can handle array [np.array ()] as an argument. The behavior is the same except for handling arrays.

import numpy as np
import matplotlib.pylab as plt

def step_function(x):
  y = x > 0
  return y.astype(np.int)

x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

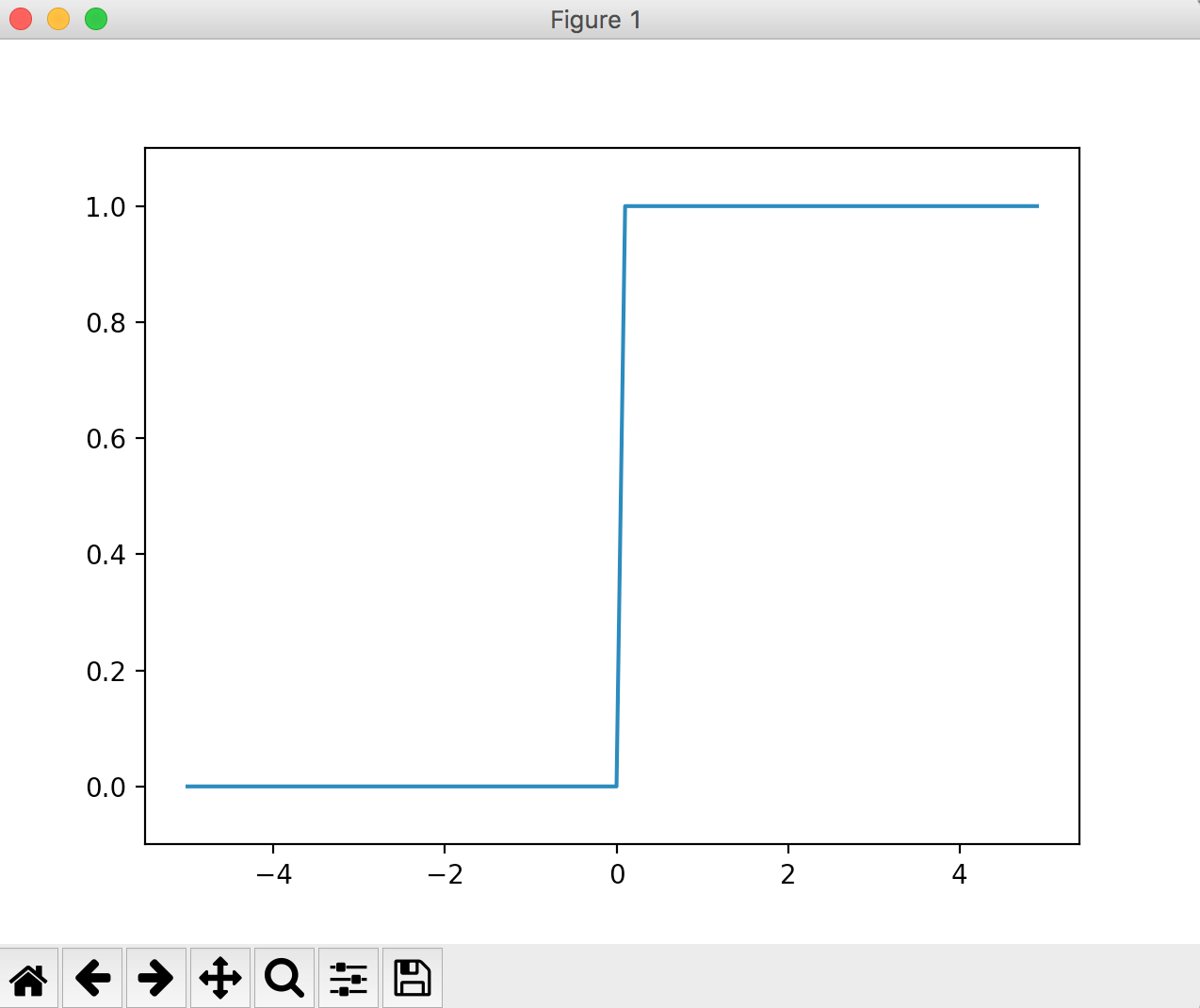
Sigmoid function

The formula is as follows.

h(x) = \frac{1}{1+e^{-x}}\\
e^{-x}Is np in numpy.exp(-x)Can be written.

The larger the value you enter, the closer to 1 The smaller the value you enter, the closer it is to 0. It can be said that the output of the step function does not kill too much the value of the original input compared to being 0 or 1.

The implementation and operation are as follows.

import numpy as np

def sigmoid(x):
  return 1 / (1+np.exp(-x))

x = np.array([-3.0, 1.0, 4.0])
# sigmoid(x) => [ 0.04742587  0.73105858  0.98201379]

The graph looks like this:

import numpy as np
import matplotlib.pylab as plt

def sigmoid(x):
  return 1 / (1+np.exp(-x))

x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

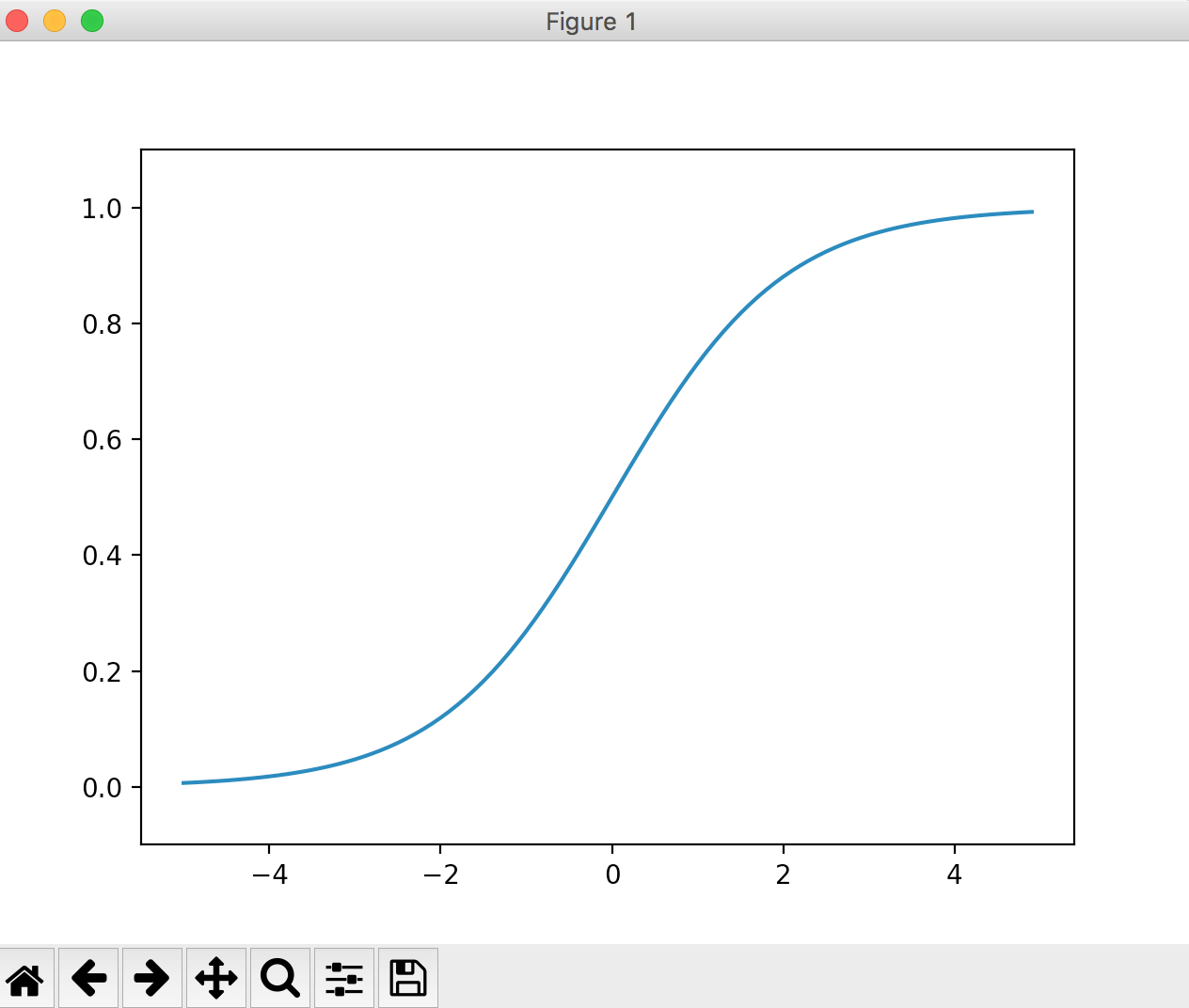
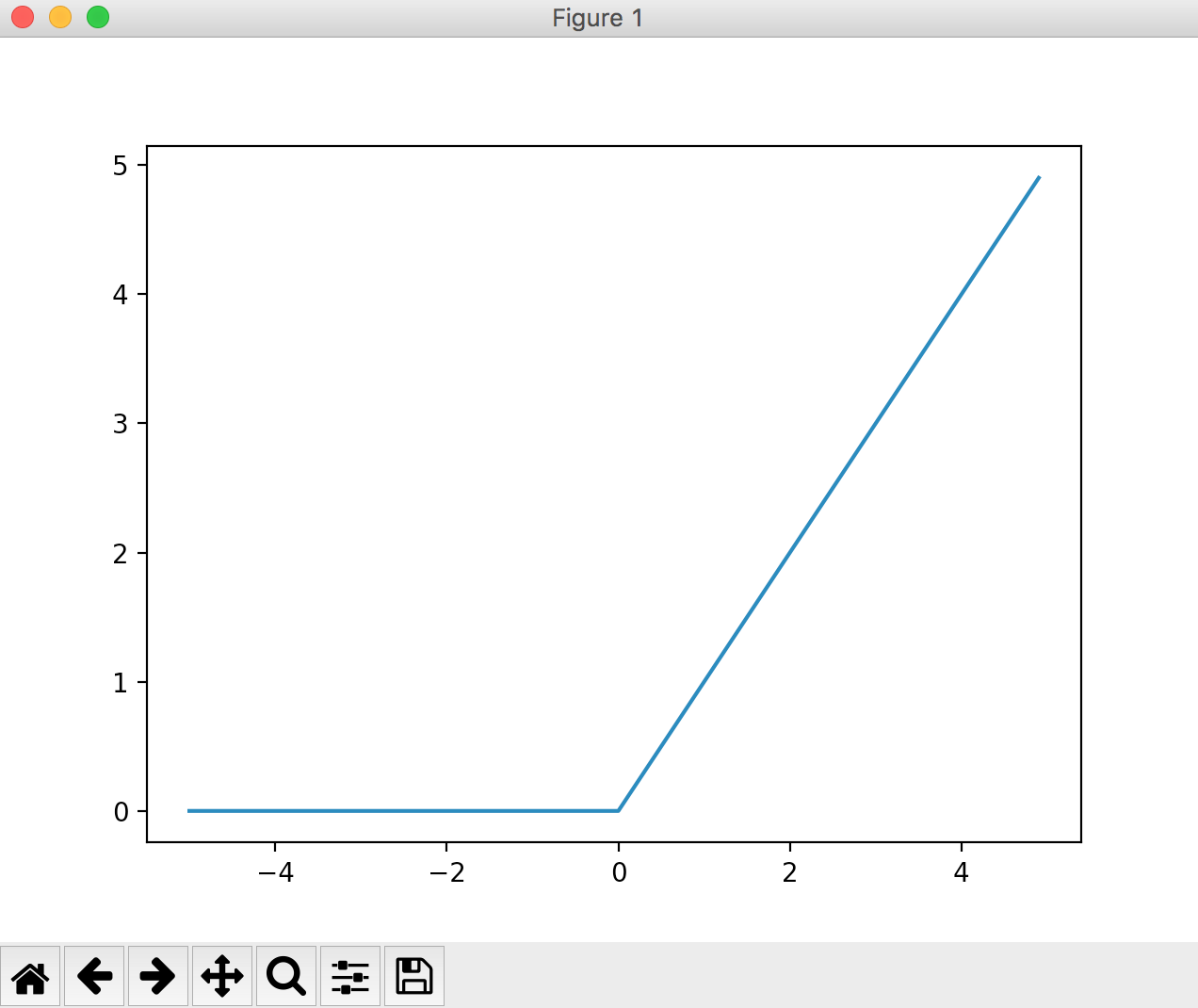
ReLU function

When the input value is 0 or less, it becomes 0, and when it is larger than 1, the input is output as it is. The graph will look like the one below.

import numpy as np
import matplotlib.pylab as plt

def relu(x):
  return np.maximum(0, x)

x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.show()

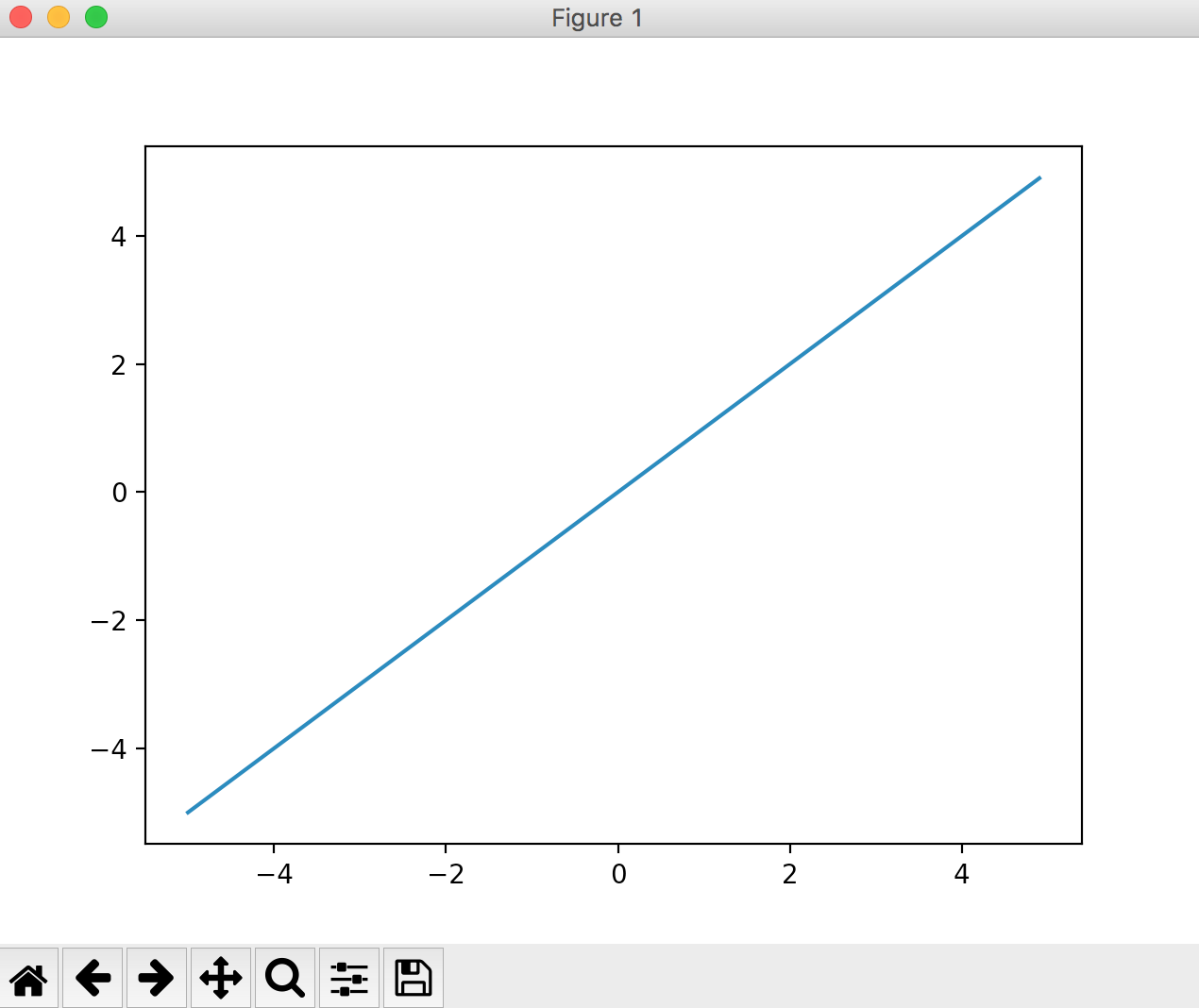
Identity function

A function used in the output layer. This function always returns the same value as the input value. [Question] Mathematics: What is an identity function

Commonly used in regression problems.

import numpy as np
import matplotlib.pylab as plt

def koutou(a):
  return a

x = np.arange(-5, 5, 0.1)
y = koutou(x)
plt.plot(x, y)
plt.show()

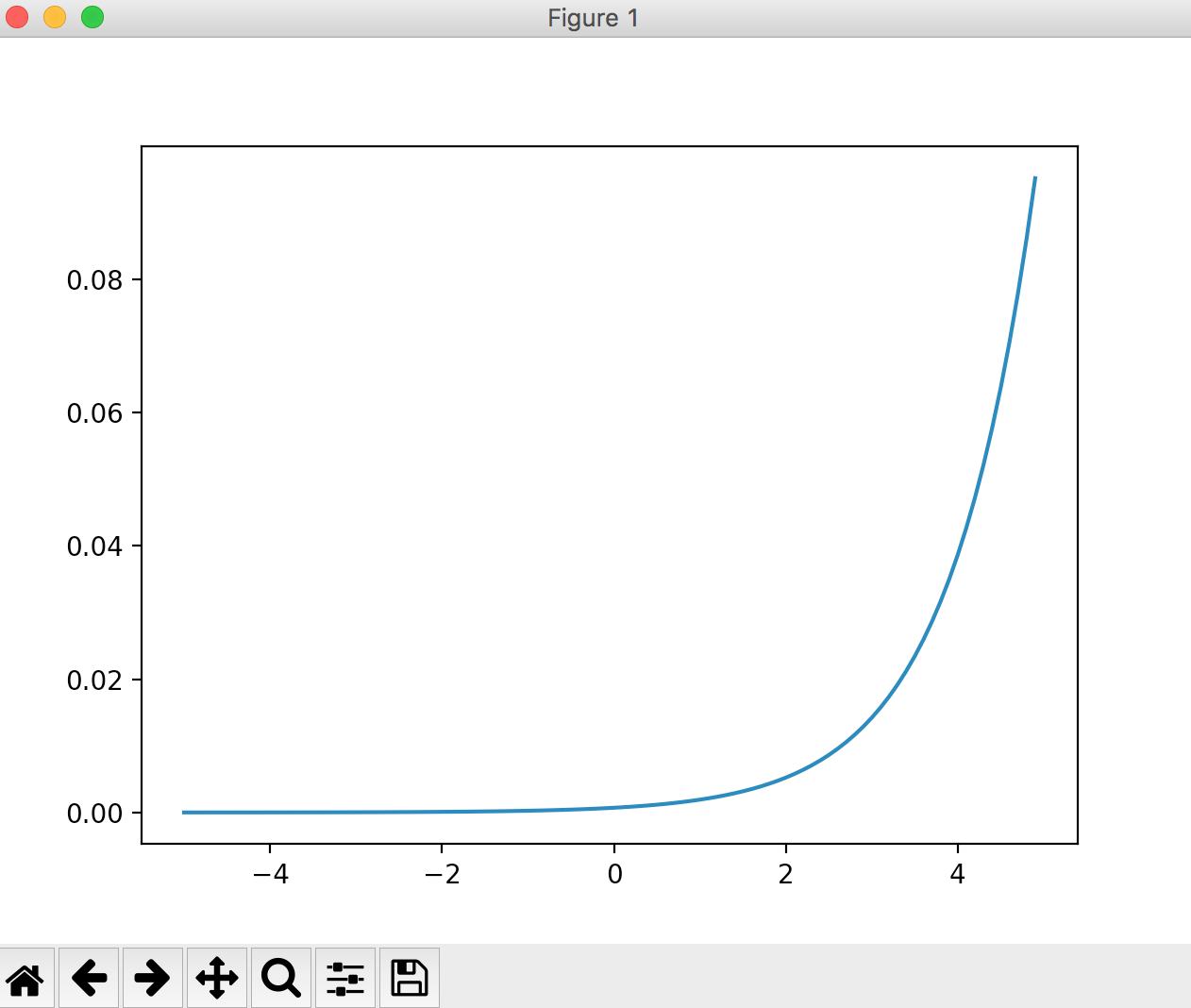
Softmax function

A function used in the output layer. Commonly used in classification problems.

import numpy as np
import matplotlib.pylab as plt

def softmax(a):
  exp_a = np.exp(a)
  sum_exp_a = np.sum(exp_a)
  y = exp_a / sum_exp_a
  return y

x = np.arange(-5, 5, 0.1)
y = softmax(x)
plt.plot(x, y)
plt.show()

Linear and non-linear functions

A linear function is a function whose output is a constant multiple of the input. For example, y = cx (c is a constant). If you make a graph, it will be a straight line.

Non-linear functions are those that are not linear functions.

Why not use linear functions in Multilayer Perceptron?

The reason is that using a linear function as the activation function makes it meaningless to deepen the layer in a neural network. The problem with linear functions is due to the fact that no matter how deep the layers are, there is always a "network without hidden layers" that does the same thing. As a simple example, if the linear function h (x) = cx is used as the activation function and three layers are stacked, it becomesy = h (h (h (x)). That is, this isy = c *. It can be expressed even in a network without a hidden layer, such as c * c * x (y = ax).

If you use a linear function as the activation function as in this example, you cannot take advantage of the multiple layers. In other words, you should not use linear functions for the activation function, as it may lead to unnecessary processing.

Regression problem and classification problem

Regression problems are problems that make (continuous) numerical predictions from some input data. (Example: The problem of predicting the weight of a person from an image of the person)

The classification problem is the question of which class the data belongs to. (Example: A problem that classifies whether a person is male or female from an image of a person)

Summary of activation functions (step, sigmoid, ReLU, softmax, identity function)