Publié un article pour la première fois comme une histoire de recherche d'emploi.

J'ai lu et mis en œuvre le document IIC (Invariant Information Clustering), qui est dit très précis. IIC est une méthode de regroupement en maximisant la quantité d'informations mutuelles. Cliquez ici pour les articles de l'IIC (https://arxiv.org/pdf/1807.06653.pdf#page9)

Invariant Information Clustering for Unsupervised Image Classification and Segmentation Xu Ji, João F. Henriques, Andrea Vedaldi

Le framework utilisé est TensorFlow 2.0. Les données cibles sont le MNIST familier.

À propos de l'information mutuelle

Il existe plusieurs interprétations de la quantité d'informations mutuelles, mais je choisirai une méthode simple et facile à expliquer cet apprentissage automatique.

L'entropie d'information H (X) pour la distribution de probabilité X est définie ci-dessous.

H(X) = -\sum_{i}x_{i} \ln x_{i}

La valeur de ce montant augmente à mesure que la distribution s'approche d'une distribution uniforme et devient 0 lorsque la distribution converge vers un point. On peut dire que le montant d'information mutuelle $ I $ est le montant auquel correspondent les ensembles d'entropie d'information des deux distributions de probabilité ** non indépendantes ** $ X $ et $ Y $.

I(X, Y) = H(X) + H(Y) - H(X,Y)

Comme vous pouvez le voir sur la figure, maximiser le montant d'information mutuelle $ I $ rapproche l'entropie d'information de $ X $ et $ Y $, et augmente l'entropie d'information de $ X $ et $ Y $. En rapprochant l'entropie de l'information, l'apprentissage de l'expression du réseau progresse, et en augmentant l'entropie de l'information, on a pour effet d'empêcher le clustering de se concentrer sur un point (réduction).

Dans l'apprentissage réel, lorsque la sortie softmax du réseau pour la paire d'images ($ X $, $ X ') est ( Z $, $ Z' $), la probabilité simultanée de $ Z $, $ Z '$ est calculée. Maximise la quantité d'informations mutuelles sur les probabilités marginales $ P_ {x}, P_ {y} $ de la matrice symétrique $ P $. La formule spécifique de la fonction de perte est la suivante.

\begin{align}
I(P_{x}, P_{y}) &= -\sum_{i}P_{x(i)} \ln P_{x(i)}-\sum_{j}P_{y(j)} \ln P_{y(j)}+\sum_{i}\sum_{j}P_{(i, j)} \ln P_{(i, j)}\\
&=\sum_{i}\sum_{j}\bigl(P_{(i, j)}(-\ln P_{x(i)}-\ln P_{y(j)}+\ln P_{(i, j)})\bigr)\\
&=\sum_{i}\sum_{j}P_{(i, j)}・\ln \frac{P_{(i, j)}}{P_{x(i)} P_{y(j)}}
\end{align}

Faire une paire d'images

Pour apprendre, il faut faire une paire de $ X '$ pour l'image $ X $. $ X $, $ X '$ sont des paires de données contenant le même objet, mais il est souhaitable que les détails spécifiques à l'instance soient différents. Le fait est que la sortie $ Z, Z '$ du réseau est fortement dépendante et non indépendante car ce sont la même paire d'objets.

Généralement, $ X $ est transformé en $ X '$ en ajoutant des opérations telles que la mise à l'échelle, l'inclinaison (distorsion), la rotation, l'inversion et la modification du contraste et de la saturation. Cette fois, les 4 opérations suivantes ont été effectuées.

Image d'origine	Rotation	distorsion	Binarisation	bruit

Cette opération affectera grandement l'apprentissage.

Structure du réseau

Inutile de dire qu'il vaut mieux faire l'apprentissage par transfert, mais cette fois c'est une tâche simple, j'ai donc simplement créé une forme familière de Conv et BN. Produit un vecteur de prédiction softmax pour une image d'entrée 28x28x1. La sortie $ Z $ est un clustering MNIST, 10 dimensions égales au nombre d'étiquettes. L'autre est la sortie utilisée dans le papier appelé Overclustering, qui est de 50 dimensions, cinq fois l'étiquette. Le surclassement est un mécanisme dans lequel le réseau acquiert plus de fonctionnalités en effectuant simultanément plus de clustering que le nombre prévu de clustering. Les poids des couches de convolution sont partagés pour ces deux apprentissages, mais les couches entièrement connectées utilisent des poids différents.

def create_model(self):
    inputs = layers.Input((28,28,1))

    x = layers.Conv2D(32, 3, padding="same")(inputs)
    x = layers.BatchNormalization()(x)
    x = layers.Activation("relu")(x)
    x = layers.MaxPooling2D(2)(x)

    x = layers.Conv2D(64, 3, padding="same")(x)
    x = layers.BatchNormalization()(x)
    x = layers.Activation("relu")(x)
    x = layers.MaxPooling2D(2)(x)

    x = layers.Conv2D(128, 3, padding="same")(x)
    x = layers.BatchNormalization()(x)
    x = layers.Activation("relu")(x)
    x = layers.MaxPooling2D(2)(x)

    x = layers.Conv2D(256, 3, padding="same")(x)
    x = layers.BatchNormalization()(x)
    x = layers.Activation("relu")(x)
    conv_out = layers.GlobalAveragePooling2D()(x)

    x = layers.Dense(128, activation="relu")(conv_out)
    x = layers.Dense(64, activation="relu")(x)
    Z = layers.Dense(10, activation="softmax")(x)

    x = layers.Dense(128, activation="relu")(conv_out)
    x = layers.Dense(64, activation="relu")(x)
    overclustering = layers.Dense(50, activation="softmax")(x)

    return Model(inputs, [Z, overclustering])

Définition de la fonction de perte

Donnez les données de lot du modèle des paires d'images $ X, X '$, obtenez la sortie de $ Z, Z' $ et Overclustering, et calculez la quantité d'informations mutuelles de chacune avec la méthode IIC. L'article a un exemple d'implémentation dans Pytrch, et une fois réécrit vers TenosrFlow 2.0, il devient le code suivant. Nous visons à maximiser la quantité d'informations mutuelles, mais comme l'apprentissage automatique la minimise, nous multiplions la fonction de perte entière par un moins. La perte finale est la moyenne du clustering et du overclustering, et le gradient est calculé avec cette valeur.

def IIC(self, z, z_, c=10):
    z = tf.reshape(z, [-1, c, 1])
    z_ = tf.reshape(z_, [-1, 1, c])
    P = tf.math.reduce_sum(z * z_, axis=0)  #Probabilité simultanée
    P = (P + tf.transpose(P)) / 2  #Symétrie
    P = tf.clip_by_value(P, 1e-7, tf.float32.max)  #Biais pour éviter la divergence des journaux
    P = P / tf.math.reduce_sum(P)  #Standardisation
    
    #Probabilité périphérique
    Pi = tf.math.reduce_sum(P, axis=0)
    Pi = tf.reshape(Pi, [c, 1])
    Pi = tf.tile(Pi, [1,c])
    Pj = tf.math.reduce_sum(P, axis=1)
    Pj = tf.reshape(Pj, [1, c])
    Pj = tf.tile(Pj, [c,1])

    loss = tf.math.reduce_sum(P * (tf.math.log(Pi) + tf.math.log(Pj) - tf.math.log(P)))

    return loss

@tf.function
def train_on_batch(self, X, X_):
    with tf.GradientTape() as tape:
        z, overclustering = self.model(X, training=True)
        z_, overclustering_ = self.model(X_, training=True)
        loss_cluster = self.IIC(z, z_)
        loss_overclustering = self.IIC(overclustering, overclustering_, c=50)

        loss = (loss_cluster + loss_overclustering) / 2

    graidents = tape.gradient(loss, self.model.trainable_weights)
    self.optim.apply_gradients(zip(graidents, self.model.trainable_weights))
    return loss_cluster, loss_overclustering

Résultat d'apprentissage

Paramètres d'apprentissage l'optimiseur est le taux d'Adam 0,0001 batch_size est 1 000 Les résultats de l'apprentissage jusqu'à l'époque 100 en utilisant les paires d'images dans chaque opération de conversion sont les suivants.

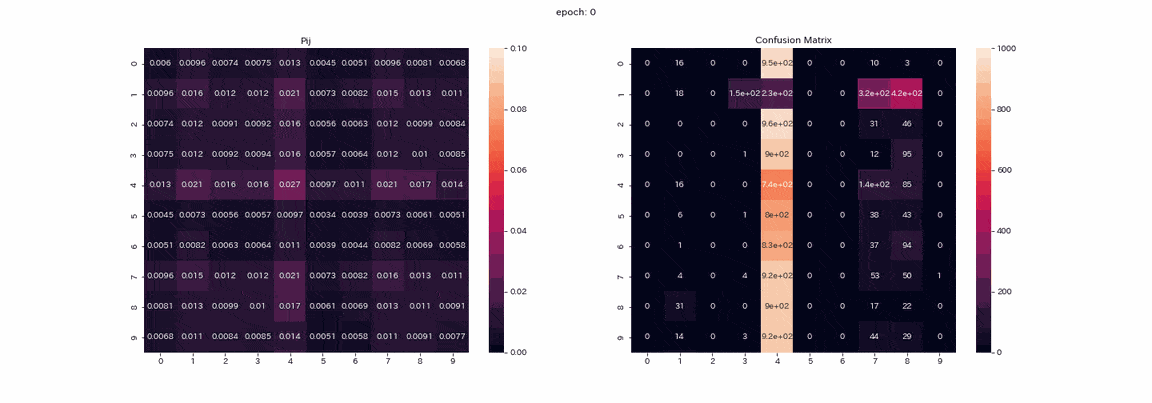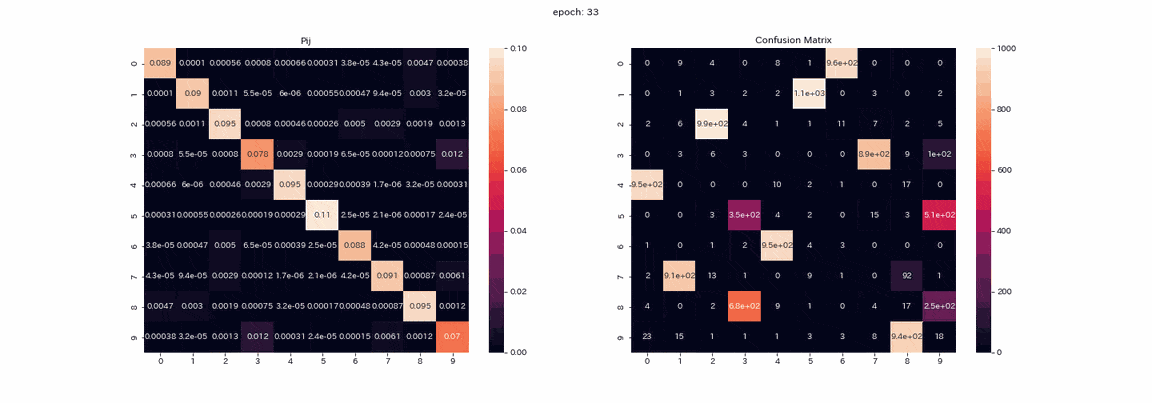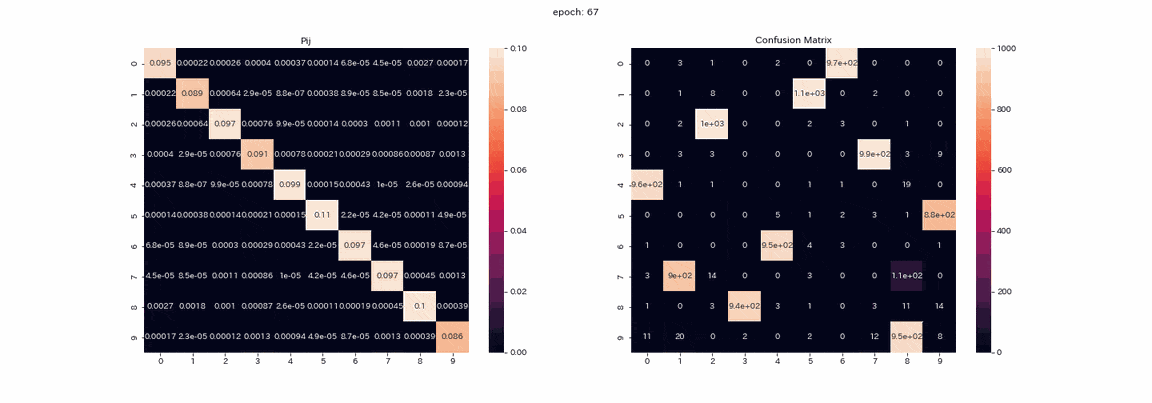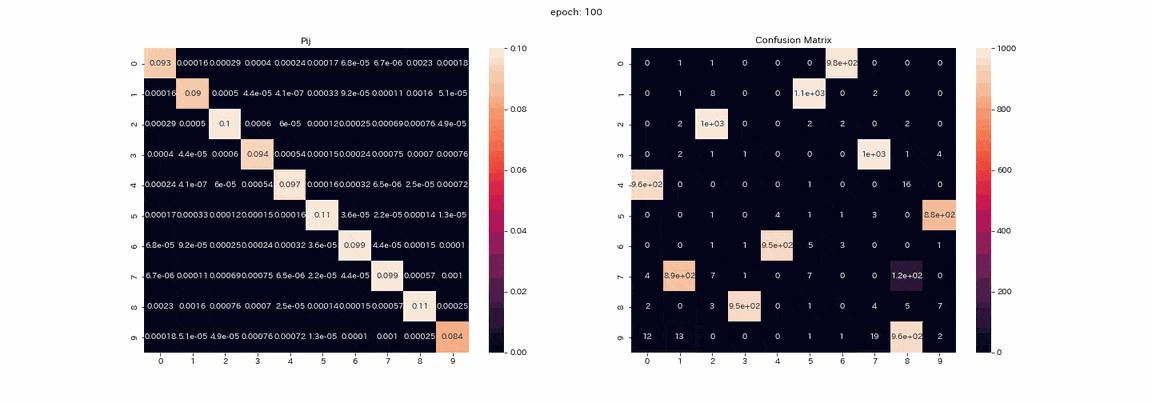
En regardant le graphique, nous pouvons voir qu'il vaut mieux combiner plusieurs conversions que d'effectuer la conversion seule. Ce qui suit est un entraînement avec une paire d'images qui a subi les quatre transformations avec les meilleurs résultats. La matrice mixte de la matrice d'apprentissage $ P $ et la prédiction des données de test (l'axe vertical est la vraie étiquette, l'axe horizontal est l'indice de sortie). ) Est un gif enregistré.

En fait, j'ai appris plus de 500 époques, mais je pense que l'apprentissage était presque terminé car il n'y avait pas beaucoup de changement dans plus de 100 époques. Dans la matrice $ P $, les valeurs sont disposées en diagonale au fur et à mesure de la progression de l'apprentissage, car $ Z et Z '$ produiront la même distribution. Vous pouvez également voir que la valeur de la colonne 1 est supérieure aux autres. Les étiquettes 2 et 3 ne peuvent pas être distinguées dans la matrice mixte, et il y a deux colonnes qui produisent l'étiquette 8. Bien qu'il ne soit pas parfait, le taux de réponse correcte était de 85% sans enseignant.

Amélioration

Maintenant, c'est une bonne idée de trouver une conversion qui rend mieux $ X '$ afin d'augmenter le taux de précision, mais nous améliorerons la précision en concevant la fonction de perte. En regardant le processus d'apprentissage plus tôt, il semble que la cause de l'erreur de clustering soit que les probabilités périphériques de la matrice $ P $ ne soient pas égales. Si vous vérifiez la formule pour la quantité d'informations mutuelles, vous pouvez voir que les termes $ H (X) et H (Y) $ égalisent les probabilités marginales. Par conséquent, j'ai décidé d'ajouter un poids alpha à cette section et de l'utiliser comme paramètre.

    #perte plus alpha
    loss = tf.math.reduce_sum(P * (alpha * tf.math.log(Pi) + alpha * tf.math.log(Pj) - tf.math.log(P)))

Le résultat de l'apprentissage avec alpha réglé sur 10 est le suivant.

![rsbn_loss_matrix-compressor.gif](https://qiita-image-store.s3.ap-northeast-1.amazonaws.com/0/340563/7c501a33-c153-b365-5d7e-7e8cea89fa58.gif)

L'apprentissage est stable et presque tous les regroupements réussissent. Le taux de réponse correcte le plus élevé était d'environ 97,5%, ce qui était tout à fait exact.

prime

J'étais curieux de savoir quel type de classification Overclustering est, alors vérifiez-le. Vous trouverez ci-dessous une matrice mixte de surclassement (50 dimensions) dans le modèle le plus précis. Il peut être confirmé que toutes les étiquettes peuvent également être classées ici. Une partie des colonnes 9, 23, 40 de l'étiquette 7 est affichée.

Colonne 9	Colonne 23	Colonne 40

Chacun saisit les caractéristiques de la façon d'écrire «7». La différence entre les colonnes 9 et 40 est-elle l'épaisseur de la ligne? Lorsque j'ai recherché d'autres nombres, les groupes étaient souvent séparés en raison de la différence d'épaisseur, mais cela semble être dû à la nature de la couche convolutive. C'est la colonne 23 à laquelle je voudrais prêter attention. J'ai tout vérifié, mais presque tous les «7» écrits en deux traits, que je ne connais pas, entrent dans la colonne 23. J'ai senti que pouvoir classer et récupérer ce «7» avait le potentiel de créer de nouvelles étiquettes au-delà des données de l'enseignant.

Le document de la SII montre que c'est une méthode qui peut également être appliquée à la segmentation, et il semble qu'elle puisse être appliquée à diverses tâches tant que la quantité d'informations mutuelles peut être calculée. C'était une méthode pleine de performances romantiques qui ne nécessitait pas de données d'enseignants.

Une méthode simple pour obtenir le taux de réponse correct de MNIST de 97% ou plus en apprenant sans enseignant (sans apprentissage par transfert)