(complexe) Cela dépend de la façon de nommer le coefficient de l'ondelette de morlet, de la valeur de réglage appropriée et du matériau, j'ai donc essayé de l'organiser autant que possible.
Je ne peux pas vraiment l'organiser, mais ...
1. Je ne sais pas si les variables et expressions de l'expression d'ondelettes sont légèrement différentes et pointent exactement vers la même chose.
ref. D'après le matériel de matlab (probablement) Teolis (1998) Traitement du signal informatique avec ondelettes. P66
formule
Nom de variable
γb: variance nommée (largeur de bande). Identique à fb dans le matériau matlab. Cela semble être une dispersion temporelle. Mais qu'est-ce que la dispersion temporelle ici? Elle s'appelle γc: fréquence centrale. C'est presque la même. Je comprends que c'est la valeur fixée par factor = np.arange (8,30) comme mne. j: unité imaginaire
ref. stack overflow
formule
w (t, f 0 </ sub>) = A ・ exp (−t 2 </ sup> / 2 * σ 2 </ sup>) ・ exp (2 * i * π * f 0 </ sub> * t) = A ・ exp (2 iπ f 0 </ sub> t- (t 2 </ sup> / 2σ 2 </ sup> >))
variable
f 0 </ sub>: fréquence centrale (γc ci-dessus, fc dans la boîte à outils d'ondelettes matlab) Il est décrit comme σ: σ = m / 2πf 0 </ sub>. Comme décrit dans [Tallon-Baudry (1999)] 3, la signification de l'écart type (sigmat) par rapport au temps. Par rapport à l'équation de Teolis (1998) ci-dessus, Cela correspond en supposant que γb = 2σ 2 </ sup>. m: constant. Compromis entre la résolution temporelle et fréquentielle. Je l'ai mis à 7. A = 1 / (σ (2π) 0,5 </ sup>) = 1 / (σ√2π): La partie avant e (exp) est remplacée par une variable. Introduite sous le nom de facteur de normalisation Oui.
réf. [Tallon-Baudry (1999)] 3, p154 Encadré 2 Description
formule
w (t, f) = A. exp (- t 2 </ sup> / 2σ t </ sub> 2 </ sup>). exp (2i π ft): C'est Identique au débordement de pile.
variable
f: Identique à f 0 </ sub> ci-dessus. Fréquence centrale σ t </ sub>: Identique à σ ci-dessus. Décrit comme l'écart type du domaine temporel.
** A = 1 / (σt √π) 1/2 **: Il est écrit comme un facteur de normalisation comme [stack overflow] 2. La formule est un peu différente. [Tallon-Baudry (1997)] 11 Il a la même description, on ne sait pas si c'est intentionnel ou faux + copie.
formule
ψ (x) = 1 / √πfb * ** exp (x 2 </ sup> / fb) ** * exp (2iπfcx): le copier-coller n'a pas fonctionné, alors copiez-le. Comparé aux deux ci-dessus, ** exp (x 2 </ sup> / fb) ** n'a pas de ** moins **. Cette page est la seule, donc j'ai l'impression d'avoir fait une erreur. .. D'autres correspondent à Teolis (1998), stack overflow
variable
x: identique à t ci-dessus fc: Identique à f0, f, γc ci-dessus. Fréquence centrale fb: paramètre de bande passante nommé, identique à γb dans Teolis (1998).
ref. matlab help
formule
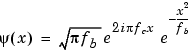C'est aussi un peu différent. Le dénominateur et la molécule sont inversés dans la partie avant e (A: facteur de normalisation qui apparaît ci-dessus). La différence entre le dénominateur et la molécule n'est que cette page, donc c'est probablement faux.
D'autres correspondent à Teolis (1998), stack overflow
variable
Le nom de fc et fb est le même que [matlab wavelet toolbox] 4
réf. [Échange de pile] 7 wavelet cmor fb fc ou quelque chose comme ça va frapper le dessus.
formule
Le moins de e -j2pifct </ sup> semble inutile.
Résumé de 1
Jugement complet (complexe) La formule d'ondes de Morlet est Teolis (1998) Computational Signal Proceesing with Wavelets. P66, Stack overflow semble correct. Teolis (1998) est un texte. La formule est vraiment légèrement différente selon le matériau, et j'ai l'impression qu'elle est en fait pleine d'erreurs.
2. Quel est un bon paramètre pour les ondelettes. (Principalement avec mne python à l'esprit)
[sortie sur le terrain] 9(analyse temps-fréquence, section d'ondelettes)
cfg.width. Il détermine la ** largeur ** des ondelettes en nombre de cycles. Dans l'échantillon
cfg.width = 7;
C'était. Aussi, The spectral bandwidth at a given frequency F is equal to F/width*2 the wavelet duration is equal to width/F/pi F est la fréquence, qui semble être la même que la fréquence centrale (f, f 0 </ sub>, γc, fc) ci-dessus.
--Je ne sais tout simplement pas ce que signifient la bande passante spectrale et la durée des ondelettes. --Il semble que ce n'est pas une relation si simple que la bande passante spectrale corresponde à σ f </ sub> et que la durée de la forme d'onde corresponde à σ t </ sub>. Il existe de nombreux termes et c'est déroutant.
Tallon-Baudry(1999) ** σ f </ sub> = 1 / (2πσ t </ sub>) ** (Équation 2.1) La relation est montrée.
--σ t </ sub> est décrit comme un écart type (domaine temporel) .Il semble être le même que σ t </ sub> et σ qui sont apparus plusieurs fois. --σ f </ sub> est également décrit comme un écart type (domaine fréquentiel).
** f / σ f </ sub> (rapport constant: supérieur à cinq en pratique) ** (équation 2.2).
--f semble être la même que la fréquence centrale (F dans le champ trip, f 0 </ sub>, γc, fc qui apparaît ci-dessus).
Roach & Mathalon (2008) ** σ t </ sub> = 1 / (2πσ f </ sub>) ** (Équation 2.3) Il en est de même si l'équation (2.1) de [Tallon-Baudry (1999)] 3 est modifiée.
Description des variables
σ t </ sub>: Décrit comme SD temporel. σ f </ sub>: bande passante spectrale autour de sa fréquence centrale, f0, qui a un SD de σ f </ sub>, on peut donc dire que c'est SD de fréquence. L'ondelette de Morlet est l'enveloppe gaussienne ( Etant donné que le mot «enveloppe normalement distribuée» apparaît fréquemment, SD peut être facile à utiliser comme un index sous forme d'ondelette. Juste au bas de la même page spectral bandwidth around any given center frequency is mσf. Il y a aussi. m est multiplié. Pour en déduire spectral bandwith = mσf , and has σf in it. J'imagine que ça veut dire, je suis troublé par la description qui confond le texte.
** c = f 0 </ sub> / σ f </ sub> ** (Équation 2.4) Et ** c (rapport constant) ** sont définis ** (probablement la même chose que cfg.width) **. Cela indique également la même chose, seule la variable c est affectée à l'équation 2.2. On pense que oui.
--Il est recommandé dans le texte que c soit un nombre d'environ 5,6,7, de sorte que σ t </ sub> contienne des ondes avec un ou plusieurs cycles ("constan"). , c, est généralement recommandé pour être supérieur à 5, et est souvent mis à des valeurs de 6 ou 7, ce qui correspond à un σ t </ sub> qui, par conséquent, au moins un cycle sinusoïdal complet pour une fréquence particulière ") .- -Dans [stack overflow] 2, la formule ** σ = m / (2 π f 0 </ sub>) ** apparaît, et (σ = σ t </ sub> (Peut-être), qui correspond à l'équation (2.5) ci-dessous, il semble donc que m et le rapport constant c dans cette équation pointent vers la même chose.
Un peu à part: Explication que σ t </ sub> contient des ondes avec un ou plusieurs cycles lorsque c est d'environ 7 (peut être faux)
Lorsqu'il est transformé sous la forme de σ t </ sub> = en utilisant les équations (2.3) et (2.4)
** σ t </ sub> = c / (2πf) = c / (2π) * 1 / f ** (équation 2.5) est obtenu.
- Puisque f est la fréquence, 1 / f est le temps d'un cycle. --Donc, si c / (2π) avant 1 / f dépasse 1, alors σ t </ sub> devrait contenir des ondes avec un ou plusieurs cycles (pourquoi une telle longueur). Je ne sais pas pourquoi vous en avez besoin) mais vous pouvez répondre aux recommandations. ―― 2π = 6,28 Puisqu'il est petit, on considère que c / (2π)> 1 en c = 7 et σ t </ sub> comprend des ondes à plus d'une période.
** Variable inconnue m **
[Roach & Mathalon (2008)] 10 l'explique comme un facteur m. ** fenêtre temporaire pour toute fréquence donnée (f 0 </ sub>) est m σ t </ sub> ** (équation 2.6) Je ne sais pas à quoi se réfère la fenêtre temporelle. Cependant, j'estime que la fenêtre temporelle est la même que la durée de l'ondelette qui apparaît dans [field trip] 9 Transformons l'expression.
À partir des équations (2.6) et (2.5) fenêtre temporelle = mc / (2π) * 1 / f = mc / (2π) / f. Je répète la description dans la section sortie sur le terrain ci-dessus,
** durée des ondelettes ** est égale à ** largeur / F / pi ** (équation 2.7) Puisque F = f, en supposant c = largeur et m = 2, fenêtre temporelle = durée de l'ondelette Tient. ** fenêtre temporaire ** (par Roach & Mathalon (2008)) ** = durée des ondelettes ** (par sortie sur le terrain) semble bonne.
[Roach et Mathalon (2008)] 10 spectral bandwidth around any given center frequency is mσf Est-ce la même chose que la bande passante spectrale dans [field trip] 9? À partir de Fieldtrip: bande passante spectrale = F / largeur * 2
Si la largeur précédente = c est correcte, alors c = f 0 </ sub> / σ f </ sub> (équation 2.4) Parce qu'il y a.
Roach & Mathalon (2008) bande passante spectrale = mσ f </ sub> = mf 0 </ sub> / c = F / largeur * m (équation de parcours) Ainsi, on peut dire que m = 2 indique la même chose.
Vous pouvez également dire que fieldtrip cfg.width = c (rapport constant).
Il y a trop de termes, c'est déroutant. Au fait, il n'y a pas de description explicite correspondant à ce "m" lors de la visite sur le terrain. Est-il traité de manière appropriée en interne?
- [Roach & Mathalon (2008)] 10 référence, mais pour [Tallon-Baudry (1997)] 11, "durée d'ondelette 2σ t </ sub> d'environ deux périodes d'oscillation La description "activité à f 0 </ sub>" apparaît. Il semble qu'elle soit traitée ici aussi comme m = 2.
- [Ford et al (2008)] 14 déclare que "rapport constant (σf = f / 7) et durée des ondelettes (4σ t </ sub>)" "bande spectrale de 4σ f </ sub> > .Il semble que cfg.width = 7 (rapport constant dans d'autres documents) dans fieldtrip et m = 4 dans [Roach & Mathalon (2008)] 10.
- "m est recommandé pour 6, mais il existe également des exemples d'analyse pour 4 et 2" ([Roach & Mathalon (2008)] 10).
- Vous pouvez analyser la fréquence avec tfr_morlet, mais il existe un élément de réglage comme celui appelé n_cycles. «Je ne sais pas du tout si n_cycles pointe vers c, une durée temporaire ou m dans la description« Le nombre de cycles globalement ou pour chaque fréquence ». ――Lorsque vous regardez les exemples d'analyse, vous pouvez voir 7 ou 2 ou freq / 2 ou freq / 3. "Donc je ne suis pas sûr après tout. Puisqu'il y en a 7 dans l'exemple de réglage, cela peut être le même que cfg.width de fieldtrip, ou plus."
Référence: si vous jetez un œil au script morlet que tfr_morlet utilise en interne
Il y a un morlet def dans mne / time_frequency / tfr.py dans le script
tfr.py
sigma_t = this_n_cycles / (2.0 * np.pi * f)
Par conséquent, à partir de l'équation (2.5), je pense que this_n_cycles (= n_cycles) = c (rapport constant).
Résumé de 2
--cfg.width of fieldtrip et n_cycles of mne python, c (constant ratio. Equation 2.4) in the document, m in [stack overflow] 2 semble indiquer la même chose. Comprendre la signification des paramètres " Je ne peux pas, mais j'aimerais lire le rapport constant et essayer de le comprendre autant que possible.Notez que m dans [Roach & Mathalon (2008)] 10 est différent. --σ t </ sub> est temporaire SD, qui est différente de la durée de l'ondelette (probablement = fenêtre temporaire) .Wavelet duration = mσ t </ sub> ([Roach & Mathalon (2008)] [ À partir de 10]
- De même, σ f </ sub> est la fréquence SD, qui est différente de la bande passante spectrale. Bande passante spectrale = mσ f </ sub> (d'après [Roach & Mathalon (2008)] 10)
- Comme je vois souvent le réglage de 7 y compris l'explication du rapport constant, il est préférable de voir d'abord le réglage de cfg.width et n_cycles.
- [Roach & Mathalon (2008)] m dans 10 n'est pas explicitement défini dans mne python, fieldtrip (je pense) Fieldtrip vaut m = 2. mne n'est-il pas équivalent? --Il existe un exemple d'analyse tel que n_cycles = 2 dans mne python (il peut être différent de wavelet car c'est un exemple de [source_band_induced_power] 12). On ne sait toujours pas si c'est le bon paramètre. [Roach & Mathalon (2008)] [ En 10], c s'écrit 5 ou plus, il est donc possible que n_cycles = c ne soit pas basé sur cet écart ... «Je ne comprends pas vraiment la différence entre Morlet et Morlet complexe en premier lieu, alors ne comptez pas là-dessus, examinons les matériaux un par un.
Recommended Posts