Réduction dimensionnelle des données haute dimension et méthode de traçage bidimensionnel

introduction

Cet article utilise Python 2.7, numpy 1.11, scipy 0.17, scikit-learn 0.18, matplotlib 1.5, seaborn 0.7, pandas 0.17. Il a été confirmé qu'il fonctionne sur le notebook jupyter. (Veuillez modifier correctement% matplotlib inline) Je me réfère à l'article de Sklearn Manifold learning.

Une technique appelée apprentissage multi-objets sera expliquée à l'aide d'un exemple sklearn digits. En particulier, t-SNE est une méthode appropriée pour la visualisation de données multidimensionnelles, qui est parfois utilisée dans Kaggle et similaire. En plus de la visualisation, la précision des problèmes de classification simples peut être améliorée en combinant les données d'origine et les données compressées.

table des matières

  1. Génération de données
  2. Réduction dimensionnelle axée sur les éléments linéaires
    1. Random Projection
    2. PCA
    3. Linear Discriminant Analysis
  3. Réduction dimensionnelle compte tenu des composants non linéaires
    1. Isomap
    2. Locally Linear Embedding
    3. Modified Locally Linear Embedding
    4. Hessian Eigenmapping
    5. Spectral Embedding
    6. Local Tangent Space Alignment
    7. Multi-dimensional Scaling
    8. t-SNE
    9. Random Forest Embedding

1. Génération de données

Utilisez les exemples de données de sklearn. Cette fois, nous allons regrouper les nombres à l'aide du jeu de données chiffres. Tout d'abord, chargez et vérifiez les données.

load_digit.py


from time import time

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import offsetbox
from sklearn import (manifold, datasets, decomposition, ensemble,
                     discriminant_analysis, random_projection)

digits = datasets.load_digits(n_class=6)
X = digits.data
y = digits.target
n_samples, n_features = X.shape
n_neighbors = 30

n_img_per_row = 20
img = np.zeros((10 * n_img_per_row, 10 * n_img_per_row))
for i in range(n_img_per_row):
    ix = 10 * i + 1
    for j in range(n_img_per_row):
        iy = 10 * j + 1
        img[ix:ix + 8, iy:iy + 8] = X[i * n_img_per_row + j].reshape((8, 8))

plt.imshow(img, cmap=plt.cm.binary)
plt.xticks([])
plt.yticks([])
plt.title('A selection from the 64-dimensional digits dataset')

a

Préparez une fonction pour mapper les données numériques. Ce n'est pas le sujet de cet article, alors sautez-le si vous n'êtes pas sûr.

def plot_embedding(X, title=None):
    x_min, x_max = np.min(X, 0), np.max(X, 0)
    X = (X - x_min) / (x_max - x_min)

    plt.figure()
    ax = plt.subplot(111)
    for i in range(X.shape[0]):
        plt.text(X[i, 0], X[i, 1], str(digits.target[i]),
                 color=plt.cm.Set1(y[i] / 10.),
                 fontdict={'weight': 'bold', 'size': 9})

    if hasattr(offsetbox, 'AnnotationBbox'):
        # only print thumbnails with matplotlib > 1.0
        shown_images = np.array([[1., 1.]])  # just something big
        for i in range(digits.data.shape[0]):
            dist = np.sum((X[i] - shown_images) ** 2, 1)
            if np.min(dist) < 4e-3:
                # don't show points that are too close
                continue
            shown_images = np.r_[shown_images, [X[i]]]
            imagebox = offsetbox.AnnotationBbox(
                offsetbox.OffsetImage(digits.images[i], cmap=plt.cm.gray_r),
                X[i])
            ax.add_artist(imagebox)
    plt.xticks([]), plt.yticks([])
    if title is not None:
        plt.title(title)

2. Réduction dimensionnelle axée sur les composants linéaires

La méthode présentée ici a un faible coût de calcul et une grande polyvalence, et est fréquemment utilisée. Par exemple, l'ACP est une méthode très pratique qui permet d'extraire la corrélation des données. Ces méthodes sont expliquées en détail sur de nombreux sites, alors jetons un coup d'œil rapide.

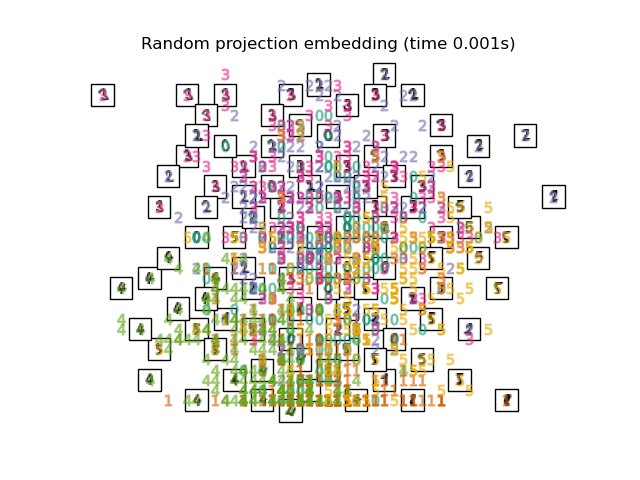
2.1. Random Projection J'ai eu 64 données numériques dimensionnelles en 1. La méthode la plus élémentaire pour cartographier ces données de grande dimension est la projection aléatoire. En utilisant une méthode très simple, les éléments de la matrice R qui mappe des données M-dimensionnelles à N-dimensionnelles mappables sont définis avec des nombres aléatoires. Le mérite est le faible coût de calcul.

print("Computing random projection")
rp = random_projection.SparseRandomProjection(n_components=2, random_state=42)
X_projected = rp.fit_transform(X)
plot_embedding(X_projected, "Random Projection of the digits")
#plt.scatter(X_projected[:, 0], X_projected[:, 1])

b

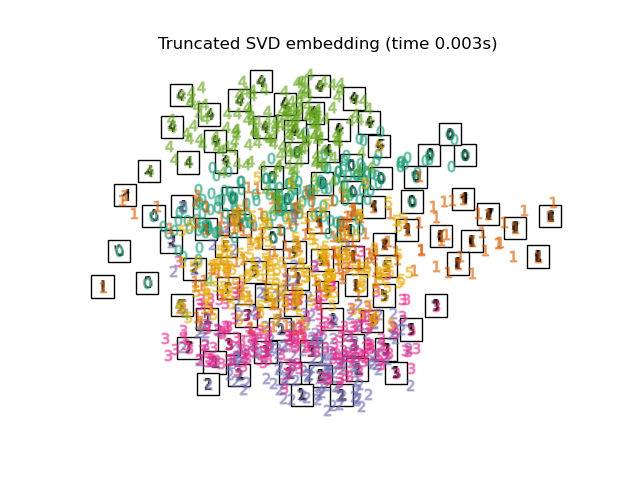
2.2. PCA Mapper avec PCA, qui est une méthode de compression de dimension générale. Extrayez le composant de corrélation entre les variables. La fonction utilisée est le SVD tronqué de sklearn, et la différence avec PCA semble être de normaliser les données d'entrée.

print("Computing PCA projection")
t0 = time()
X_pca = decomposition.TruncatedSVD(n_components=2).fit_transform(X)
plot_embedding(X_pca,
               "Principal Components projection of the digits (time %.2fs)" %
               (time() - t0))

c

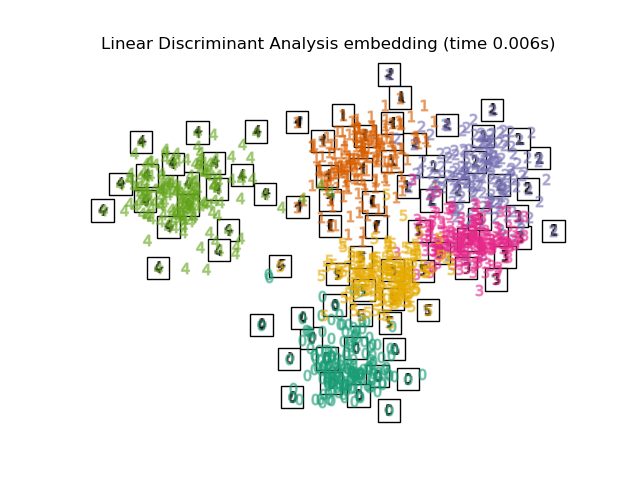
2.3. Linear Discriminant Analysis La réduction de dimension est effectuée par Classification de discrimination linéaire. La distance de Maharanobis est utilisée en supposant que chaque variable a une distribution normale multivariée et que le même groupe a la même matrice de covariance. Similaire à l'ACP, mais il s'agit d'un apprentissage supervisé.

print("Computing Linear Discriminant Analysis projection")
X2 = X.copy()
X2.flat[::X.shape[1] + 1] += 0.01  # Make X invertible
t0 = time()
X_lda = discriminant_analysis.LinearDiscriminantAnalysis(n_components=2).fit_transform(X2, y)
plot_embedding(X_lda,
               "Linear Discriminant projection of the digits (time %.2fs)" %
               (time() - t0))

d

3. Réduction dimensionnelle compte tenu des composants non linéaires

Les trois méthodes introduites précédemment ne conviennent pas pour réduire les dimensions des données avec une structure hiérarchique et des données contenant des composants non linéaires. Ici, nous allons introduire un tracé bidimensionnel de données de corrélation non linéaires telles que le swiss roll.

download (2).png

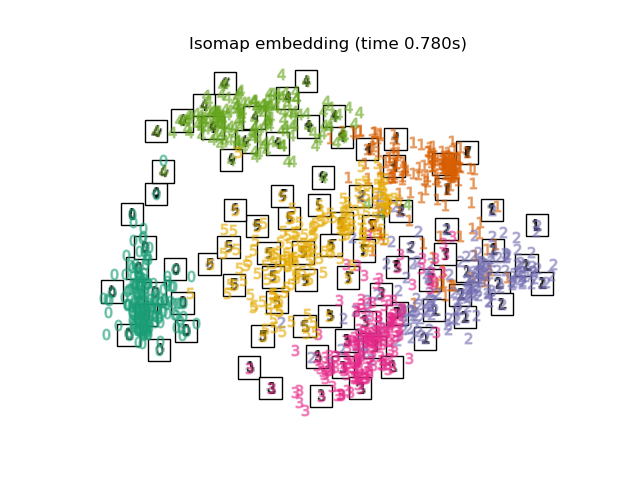
3.1. Isomap Isomap est l'une des méthodes de réduction de dimension et de regroupement prenant en compte la non-linéarité. La mise à l'échelle multidimensionnelle est effectuée sur la base du calcul de la distance mesurée le long de la forme de la variété. Il peut être exécuté avec la fonction Isomap de Sklearn. BallTree est utilisé au stade du calcul de la distance mesurée.

print("Computing Isomap embedding")
t0 = time()
X_iso = manifold.Isomap(n_neighbors, n_components=2).fit_transform(X)
print("Done.")
plot_embedding(X_iso,
               "Isomap projection of the digits (time %.2fs)" %
               (time() - t0))

3.2. Locally Linear Embedding (LLE) Dans son ensemble, même une variété qui inclut la non-linéarité. Une méthode de réduction de dimension basée sur l'intuition de la linéarité lorsqu'elle est vue localement. L'étiquette 0 semble être mise en valeur, mais les autres étiquettes sont en désordre.

print("Computing LLE embedding")
clf = manifold.LocallyLinearEmbedding(n_neighbors, n_components=2,
                                      method='standard')
t0 = time()
X_lle = clf.fit_transform(X)
print("Done. Reconstruction error: %g" % clf.reconstruction_error_)
plot_embedding(X_lle,
               "Locally Linear Embedding of the digits (time %.2fs)" %
               (time() - t0))

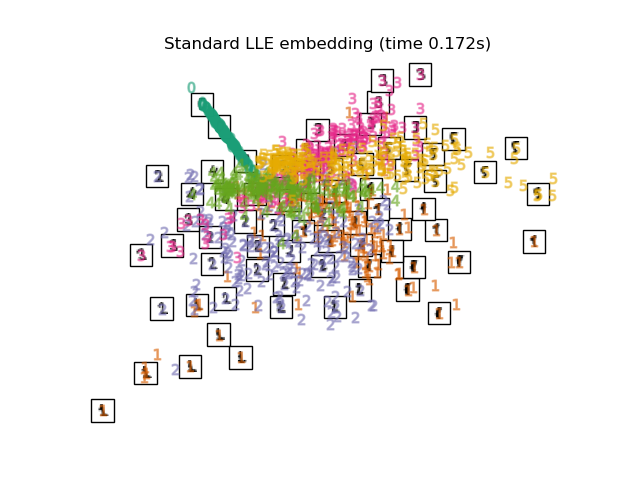
3.3. Modified Locally Linear Embedding Un algorithme qui améliore le problème de régularisation, qui est un problème de LLE. 0 Les étiquettes sont clairement classées. Les étiquettes 4, 1, 5 semblent également bien mappées.

print("Computing modified LLE embedding")
clf = manifold.LocallyLinearEmbedding(n_neighbors, n_components=2,
                                      method='modified')
t0 = time()
X_mlle = clf.fit_transform(X)
print("Done. Reconstruction error: %g" % clf.reconstruction_error_)
plot_embedding(X_mlle,
               "Modified Locally Linear Embedding of the digits (time %.2fs)" %
               (time() - t0))

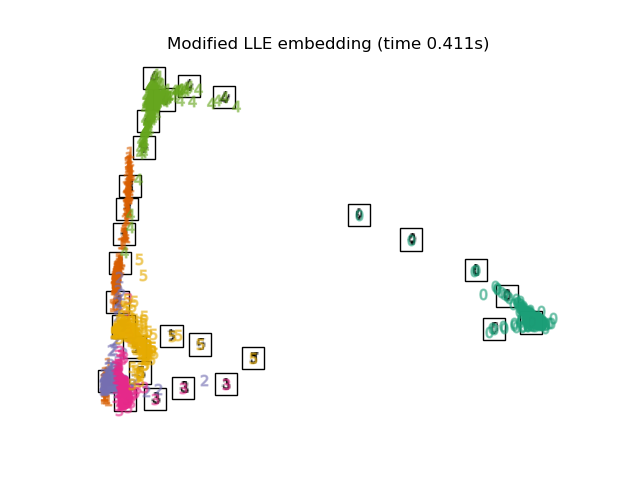
3.4. Hessian LLE Embedding Un algorithme qui améliore le problème de régularisation, qui est un problème de LLE. Partie 2

print("Computing Hessian LLE embedding")
clf = manifold.LocallyLinearEmbedding(n_neighbors, n_components=2,
                                      method='hessian')
t0 = time()
X_hlle = clf.fit_transform(X)
print("Done. Reconstruction error: %g" % clf.reconstruction_error_)
plot_embedding(X_hlle,
               "Hessian Locally Linear Embedding of the digits (time %.2fs)" %
               (time() - t0))

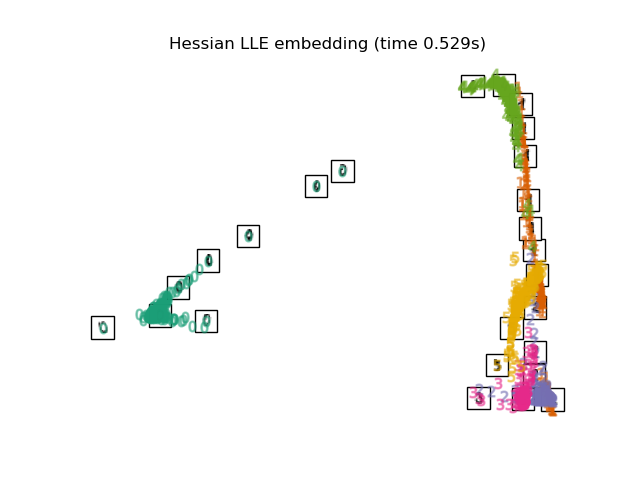
3.5. Spectral Embedding Il s'agit d'une méthode de compression également appelée laplacian Eigenmaps. Je n'ai pas étudié le contenu technique, mais il semble que j'utilise la théorie des graphes spectraux. La forme du mappage est différente de LLE, MLLE, HLLE, mais la distance et la densité entre les groupes d'étiquettes semblent être similaires.

print("Computing Spectral embedding")
embedder = manifold.SpectralEmbedding(n_components=2, random_state=0,
                                      eigen_solver="arpack")
t0 = time()
X_se = embedder.fit_transform(X)

plot_embedding(X_se,
               "Spectral embedding of the digits (time %.2fs)" %
               (time() - t0))

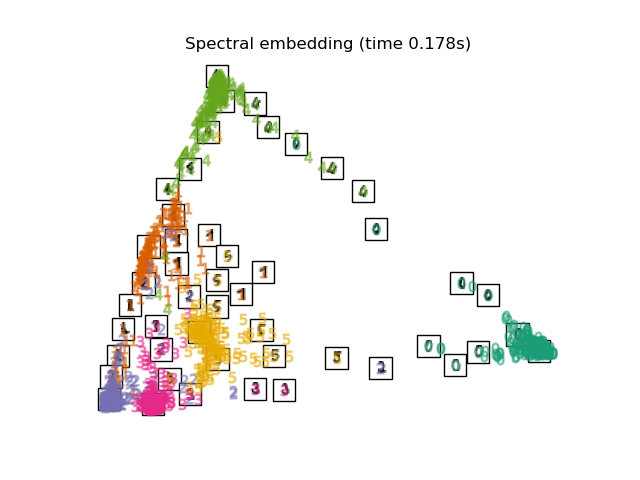
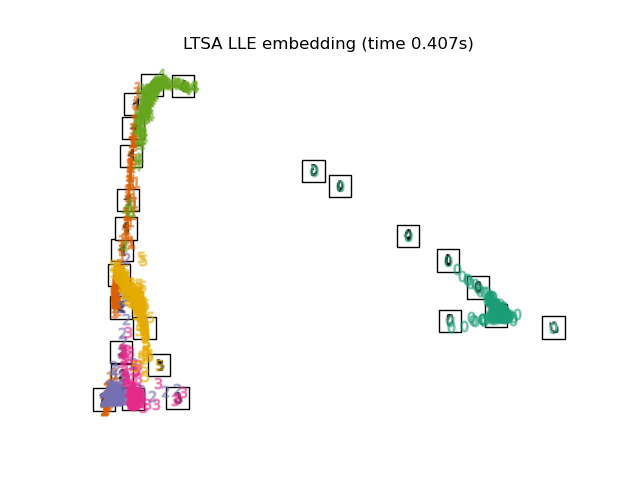
3.6. Local Tangent Space Alignment

Le résultat est comme inverser MLLE et HLLE. Les résultats de la classification sont similaires.

print("Computing LTSA embedding")
clf = manifold.LocallyLinearEmbedding(n_neighbors, n_components=2,
                                      method='ltsa')
t0 = time()
X_ltsa = clf.fit_transform(X)
print("Done. Reconstruction error: %g" % clf.reconstruction_error_)
plot_embedding(X_ltsa,
               "Local Tangent Space Alignment of the digits (time %.2fs)" %
               (time() - t0))

3.7. Multi-dimensional Scaling (MDS) [Méthode de construction à l'échelle multidimensionnelle](https://ja.wikipedia.org/wiki/%E5%A4%9A%E6%AC%A1%E5%85%83%E5%B0%BA%E5%BA%A6 Il s'agit d'une méthode de compression appelée% E6% A7% 8B% E6% 88% 90% E6% B3% 95). MDS lui-même semble être un terme général qui résume plusieurs méthodes, mais les détails ne sont pas résumés en particulier.

print("Computing MDS embedding")
clf = manifold.MDS(n_components=2, n_init=1, max_iter=100)
t0 = time()
X_mds = clf.fit_transform(X)
print("Done. Stress: %f" % clf.stress_)
plot_embedding(X_mds,
               "MDS embedding of the digits (time %.2fs)" %
               (time() - t0))

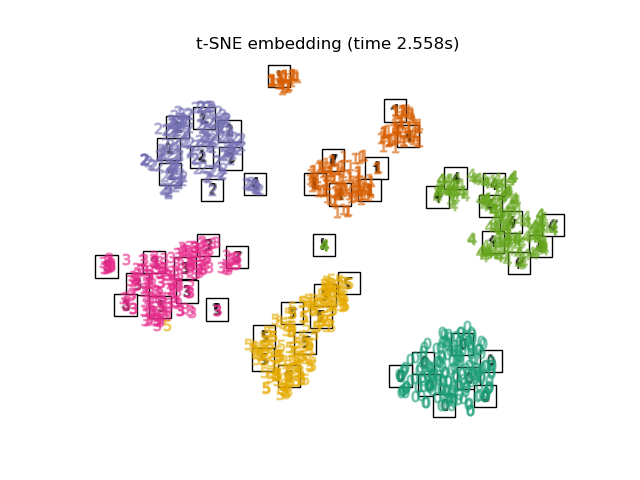
3.8. t-distributed Stochastic Neighbor Embedding (t-SNE) Il s'agit d'une méthode de conversion de la distance euclidienne de chaque point en probabilité conditionnelle au lieu de la similitude et de la mapper à une dimension inférieure.

Il existe également une méthode appelée Barnes-Hut t-SNE qui améliore le coût de calcul au détriment de la précision. Dans Sklearn, vous pouvez sélectionner deux méthodes, exacte (se concentrer sur la précision) et Barnes-Hut. Par défaut, Barnes-Hut est sélectionné et le réglage est également possible en définissant l'angle optionnel. Il est également fréquemment présenté dans Kaggle.

print("Computing t-SNE embedding")
tsne = manifold.TSNE(n_components=2, init='pca', random_state=0)
t0 = time()
X_tsne = tsne.fit_transform(X)

plot_embedding(X_tsne,
               "t-SNE embedding of the digits (time %.2fs)" %
               (time() - t0))

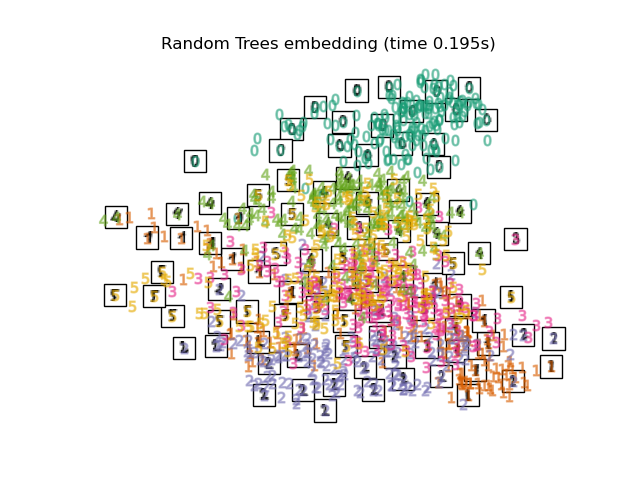
3.9. Random Forest Embedding

print("Computing Totally Random Trees embedding")
hasher = ensemble.RandomTreesEmbedding(n_estimators=200, random_state=0,
                                       max_depth=5)
t0 = time()
X_transformed = hasher.fit_transform(X)
pca = decomposition.TruncatedSVD(n_components=2)
X_reduced = pca.fit_transform(X_transformed)

plot_embedding(X_reduced,
               "Random forest embedding of the digits (time %.2fs)" %
               (time() - t0))

Recommended Posts

Réduction dimensionnelle des données haute dimension et méthode de traçage bidimensionnel
Essayez d'utiliser PHATE, une méthode de réduction et de visualisation des données biologiques
Cours Python pour la science des données - techniques utiles
Techniques Python détaillées requises pour la mise en forme des données (1)
Techniques Python détaillées requises pour la mise en forme des données (2)