Étudiez l'effet des valeurs aberrantes sur la corrélation

Aujourd'hui, nous allons nous référer au contenu du chapitre 10 "Effets des valeurs aberrantes sur le coefficient de corrélation" dans Easy Statistics by R J'expliquerai comment supprimer les valeurs aberrantes tout en examinant la corrélation. Le livre original utilisait R, mais les pandas peuvent être utilisés comme une alternative pour effectuer facilement une analyse basée sur des dataframe en Python.

Examiner le poids des animaux et le poids du cerveau

Comme dans le livre original [Données sur le poids et le poids des animaux](http://www.open.edu/openlearn/science-maths-technology/mathematics-and-statistics/mathematics/exploring-data-graphs-and- Utilisez des résumés numériques / content-section-2.7).

Tout d'abord, j'ai préparé cela sous forme de données CSV afin qu'il puisse être géré par l'ordinateur ainsi que l'autre jour (https://github.com/ynakayama/sandbox/blob) /c4720fb8ff2973314e06e8cd2342b0e8e849889f/python/pandas/animal.csv).

Importez des données CSV dans une trame de données.

animal = pd.read_csv('animal.csv')

Dessinez un diagramme de dispersion et trouvez le coefficient de corrélation

Si vous avez deux variables et que vous souhaitez examiner leur corrélation, la première étape consiste à les examiner dans un diagramme de dispersion. Comment dessiner une carte de dispersion est comme expliqué précédemment. Je vais l'essayer tout de suite.

plt.figure()
plt.scatter(animal.ix[:,1], animal.ix[:,2])
plt.savefig('animal.png')

Trouvez ensuite le coefficient de corrélation comme d'habitude.

animal.corr()
#=>
#                   Body weight (kg)  Brain weight (g)
# Body weight (kg)          1.000000         -0.005341
# Brain weight (g)         -0.005341          1.000000

La valeur du coefficient de corrélation -0,005 a été obtenue comme indiqué à la page 250 du livre original. À ce rythme, il n'y a pratiquement pas de corrélation.

Supprimer les valeurs aberrantes

Comment vérifier la valeur aberrante est comme expliqué précédemment, mais identifiez et supprimez la valeur aberrante selon le code R du livre original. Aller. Tout d'abord, il n'y a qu'un seul point sur le côté droit du diagramme de dispersion ci-dessus. C'est un dinosaure appelé Brachiosaurus au numéro 24 dans Data et pèse 80 000 kg. Les données montrent que le cerveau pèse moins de 1 000 g. Débarrassons-nous de ça.

#Sélectionnez uniquement les données pesant moins de 80000
animal2 = animal[animal.ix[:,1] < 80000]

Cela signifie sélectionner des données pesant moins de 80 000. Si vous n'ajoutez pas de référence d'index, il ne restera que moins de 80000 des données et les données non applicables seront NaN. Par conséquent, même si vous écrivez ceci, le résultat est le même.

animal2 = animal[animal < 80000].dropna()

Dans cet état, dessinez un diagramme de dispersion et trouvez le coefficient de corrélation.

animal2.corr()
#=>
#                   Body weight (kg)  Brain weight (g)
# Body weight (kg)          1.000000          0.308243
# Brain weight (g)          0.308243          1.000000

Le coefficient de corrélation est désormais de 0,30. Il y aura une corrélation positive légèrement plus faible. De plus, comme dans le livre original, retirons quatre animaux pesant plus de 2000 kg.

animal2 = animal[animal.ix[:,1] < 2000]
animal2.corr()
#=>
#                   Body weight (kg)  Brain weight (g)
# Body weight (kg)          1.000000          0.542351
#Brain weight (g)          0.542351          1.000000

plt.scatter(animal2.ix[:,1], animal2.ix[:,2])

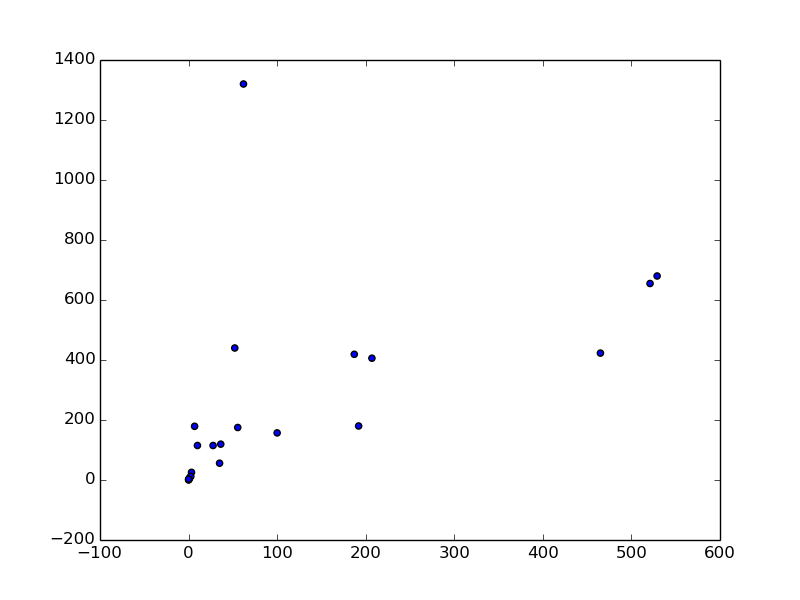
Cette fois, le coefficient de corrélation est passé à 0,54. Vous pouvez voir qu'il n'y a qu'une seule valeur aberrante dans le coin supérieur gauche du diagramme de dispersion. C'est un humain pesant moins de 100 kg et pesant plus de 1 200 g dans le cerveau. On constate que le rapport poids cérébral / poids corporel est très élevé chez l'homme par rapport aux autres animaux.

Et si les humains étaient également supprimés? Concentrez-vous sur les animaux pesant moins de 1 000 g et réexaminez.

animal3 = animal2[animal2.ix[:,2] < 1000]
#Trouvez le coefficient de corrélation
animal3.corr()
#=>
#                   Body weight (kg)  Brain weight (g)
# Body weight (kg)          1.000000          0.882234
# Brain weight (g)          0.882234          1.000000

Le coefficient de corrélation est de 0,88. À partir de là, il a été constaté qu'il existe une forte corrélation positive entre le poids du cerveau et le poids, sauf pour certains animaux.

Faites une régression linéaire

Bien que ce ne soit pas dans le livre original, nous avons obtenu une forte corrélation positive, alors trouvons l'équation de régression.

from scipy import stats
stats.linregress(animal3.ix[:,1], animal3.ix[:,2])
#=> (1.0958855201992723,
#    68.659009180996094,
#    0.88223361379712761,
#    5.648035643926062e-08,
#    0.13077177749121441)

Les valeurs de retour de scipy.stats.linregress sont inclinées comme indiqué dans SciPy Documents. , Section, coefficient de corrélation, valeur P, erreur standard.

Par conséquent, l'équation de régression (jusqu'à la deuxième minorité) est la suivante.

y = 1.10x + 68.66

Vous pouvez également voir que la valeur P est une très petite valeur.

Résumé

Les deux principales analyses de données utilisant des statistiques sont test d'hypothèse et analyse de corrélation. Il est prudent de dire qu'il s'agit des items / f5f42b5d46b97009638b). (Bien sûr, il y en a d'autres, c'est le moins qu'on puisse dire)

L'autre jour et cette fois nous avons fait une soi-disant analyse de corrélation, mais c'est la base des statistiques pour vérifier s'il existe une corrélation entre deux variables comme celle-ci. Je vais.

En formulant une hypothèse ferme sur ce qui est considéré comme étant lié et en remettant en question l'analyse des données, il est possible d'obtenir un résultat sur ce qu'est la relation statistiquement.

La prochaine fois, je résumerai le test d'hypothèse, qui est une autre méthode statistique principale pour la première fois depuis longtemps.