Apprentissage non supervisé de mnist avec encodeur automatique variationnel, clustering et évaluation des variables latentes
Apprenez mnist sans surveillance avec un encodeur et un cluster automatiques variationnels et évaluez la dernière étape
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
#Importer les bibliothèques requises
from keras.datasets import mnist
import numpy as np
import pandas as pd
import sklearn
#Afficher les résultats du tracé dans le notebook lors de l'utilisation du notebook Jupyter
import matplotlib.pyplot as plt
%matplotlib inline
from keras.layers import Lambda, Input, Dense
from keras.models import Model
from keras.losses import mse
from keras import backend as K
import gc
Using TensorFlow backend.
feature_dims = range(2, 12)
#Lire les données avec la fonction Keras. Mélangez les données et divisez-les en données d'entraînement et données d'entraînement
(x_train, y_train), (x_test, y_test) = mnist.load_data()
#Convertir les données 2D en valeur numérique
x_train = x_train.reshape(60000, 784)
x_test = x_test.reshape(10000, 784)
#Conversion de type
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
#Diviser par 255 comme nouvelle variable
x_train /= 255
x_test /= 255
# one-Méthode d'encodage à chaud
from keras.utils.np_utils import to_categorical
#10 cours
num_classes = 10
y_train = y_train.astype('int32')
y_test = y_test.astype('int32')
labels = y_test
# one-hot encoding
y_train = to_categorical(y_train, num_classes)
y_test = to_categorical(y_test, num_classes)
def fitting(feature_dim, x_train, y_train, x_test, y_test):
original_dim = x_train.shape[1]
input_shape = (original_dim, )
latent_dim = feature_dim
# Reparametrization Trick
def sampling(args):
z_mean, z_logvar = args
batch = K.shape(z_mean)[0]
dim = K.int_shape(z_mean)[1]
epsilon = K.random_normal(shape=(batch, dim), seed = 5) # ε
return z_mean + K.exp(0.5 * z_logvar) * epsilon
#Construction du modèle VAE
inputs = Input(shape=input_shape)
x1 = Dense(256, activation='relu')(inputs)
x2 = Dense(64, activation='relu')(x1)
z_mean = Dense(latent_dim)(x2)
z_logvar = Dense(latent_dim)(x2)
z = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_logvar])
encoder = Model(inputs, [z_mean, z_logvar, z], name='encoder')
encoder.summary()
latent_inputs = Input(shape=(latent_dim,))
x3 = Dense(64, activation='relu')(latent_inputs)
x4 = Dense(256, activation='relu')(x3)
outputs = Dense(original_dim, activation='sigmoid')(x4)
decoder = Model(latent_inputs, outputs, name='decoder')
decoder.summary()
z_output = encoder(inputs)[2]
outputs = [decoder(z_output),z_output]
vae = Model(inputs, outputs, name='variational_autoencoder')
#Fonction de perte
# Kullback-Leibler Loss
kl_loss = 1 + z_logvar - K.square(z_mean) - K.exp(z_logvar)
kl_loss = K.sum(kl_loss, axis=-1)
kl_loss *= -0.5
# Reconstruction Loss
reconstruction_loss = mse(inputs, outputs[0])
reconstruction_loss *= original_dim
vae_loss = K.mean(reconstruction_loss + kl_loss)
vae.add_loss(vae_loss)
vae.compile(optimizer='adam')
vae.summary()
history = vae.fit(x_train,
epochs=50,
batch_size=256,
validation_data=(x_test, None))
result = vae.predict(x_test)
K.clear_session() #← C'est
gc.collect()
from IPython.display import clear_output
clear_output()
return (history, vae, result)
#model = fitting(10, x_train, y_train, x_test, y_test)
models = [None] * len(feature_dims)
histories = [None] * len(feature_dims)
dec_imgs = [None] * len(feature_dims)
results = [None] * len(feature_dims)
for i in range(len(feature_dims)):
(histories[i], models[i], dec_imgs[i]) = fitting(feature_dims[i], x_train, y_train, x_test, y_test)
for i in range(len(feature_dims)):
print(feature_dims[i])
result = dec_imgs[i]
decoded_imgs = result[0]
#Affichage de l'image de test et de l'image convertie
n = 10
plt.figure(figsize=(10, 2))
for j in range(n):
#Afficher l'image de test
ax = plt.subplot(2, n, j+1)
plt.imshow(x_test[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
#Afficher l'image convertie
ax = plt.subplot(2, n, j+1+n)
plt.imshow(decoded_imgs[i][0][j].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
results[i] = result[1]
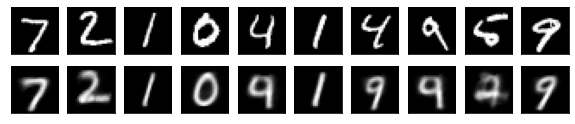
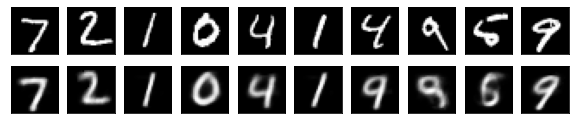

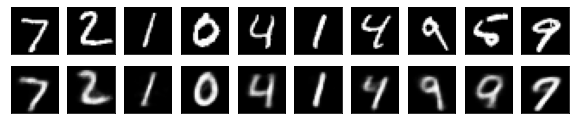
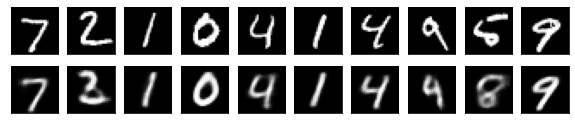
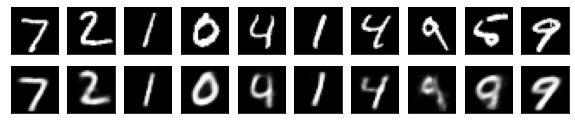
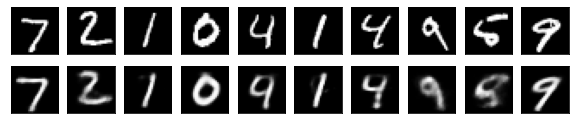
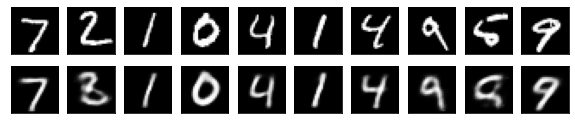
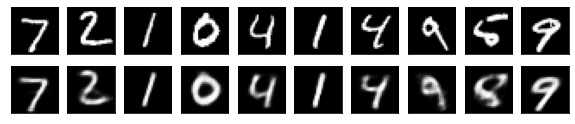
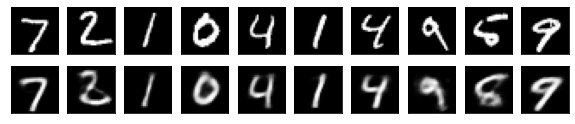
for i in range(len(feature_dims)):
results[i] = dec_imgs[i][1]
#model.save('model/mnist-10')
#model = keras.models.load_model('model/mnist-10')
#for i in range(len(feature_dims)):
# models[i].pop() #Supprimez la couche softmax à l'étape finale et utilisez la couche d'entités comme étape finale.
# models[i].summary()
#result = model.predict(x_test)
#results = [None] * len(feature_dims)
#for i in range(len(feature_dims)):
# keras.backend.clear_session()
# results[i] = models[i].predict(x_test)
def tsne(result):
#t-Réduction de dimension avec SNE
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, random_state = 0, perplexity = 30, n_iter = 1000)
return tsne.fit_transform(result)
#tsne = tsne(result)
tsnes = [None] * len(feature_dims)
for i in range(len(feature_dims)):
tsnes[i] = tsne(results[i])
#df = pd.DataFrame(tsne, columns = ['x', 'y'])
#df['label'] = labels
def km(n_clusters, result):
# k-Cluster au moyen
from sklearn.cluster import KMeans
return KMeans(n_clusters).fit_predict(result)
#km = km(10, result)
#df['km'] = km
kms = [None] * len(feature_dims)
for i in range(len(feature_dims)):
kms[i] = km(10, results[i])
def DBSCAN(n_clusters, result):
from sklearn.cluster import DBSCAN
db = DBSCAN(eps=0.2, min_samples=n_clusters).fit(result)
return db.labels_
#dbscan = DBSCAN(20, result)
#df['DBSCAN'] = dbscan
def hierarchy(result):
from scipy.cluster.hierarchy import linkage, dendrogram
result1 = linkage(result,
metric = 'braycurtis',
#metric = 'canberra',
#metric = 'chebyshev',
#metric = 'cityblock',
#metric = 'correlation',
#metric = 'cosine',
#metric = 'euclidean',
#metric = 'hamming',
#metric = 'jaccard',
#method= 'single')
method = 'average')
#method= 'complete')
#method='weighted')
return result1
#hierarchy = hierarchy(result)
#display(hierarchy)
def label_to_colors(label):
color_dict = dict([(color[0], color[1]['color']) for color in zip(np.unique(label), plt.rcParams['axes.prop_cycle'])])
colors = np.empty(label.shape, np.object)
for k, v in color_dict.items():
colors[label==k] = v
return colors
#def cluster_visualization(x, y, label, cluster, method, n_clusters):
def cluster_visualization(x, y, label, cluster):
plt.figure(figsize = (30, 15))
plt.subplot(1,2,1)
plt.scatter(x, y, c=label_to_colors(label))
# for i in range(10):
# tmp_df = df[df['label'] == i]
# plt.scatter(tmp_df['x'], tmp_df['y'], label=i)
# plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.subplot(1,2,2)
plt.scatter(x, y, c=label_to_colors(cluster))
# for i in range(n_clusters):
# tmp_df = df[df[method] == i]
# plt.scatter(tmp_df['x'], tmp_df['y'], label=i)
# plt.legend(loc='upper left', bbox_to_anchor=(1,1))
for i in range(len(feature_dims)):
cluster_visualization(tsnes[i][:,0], tsnes[i][:,1], labels, kms[i])

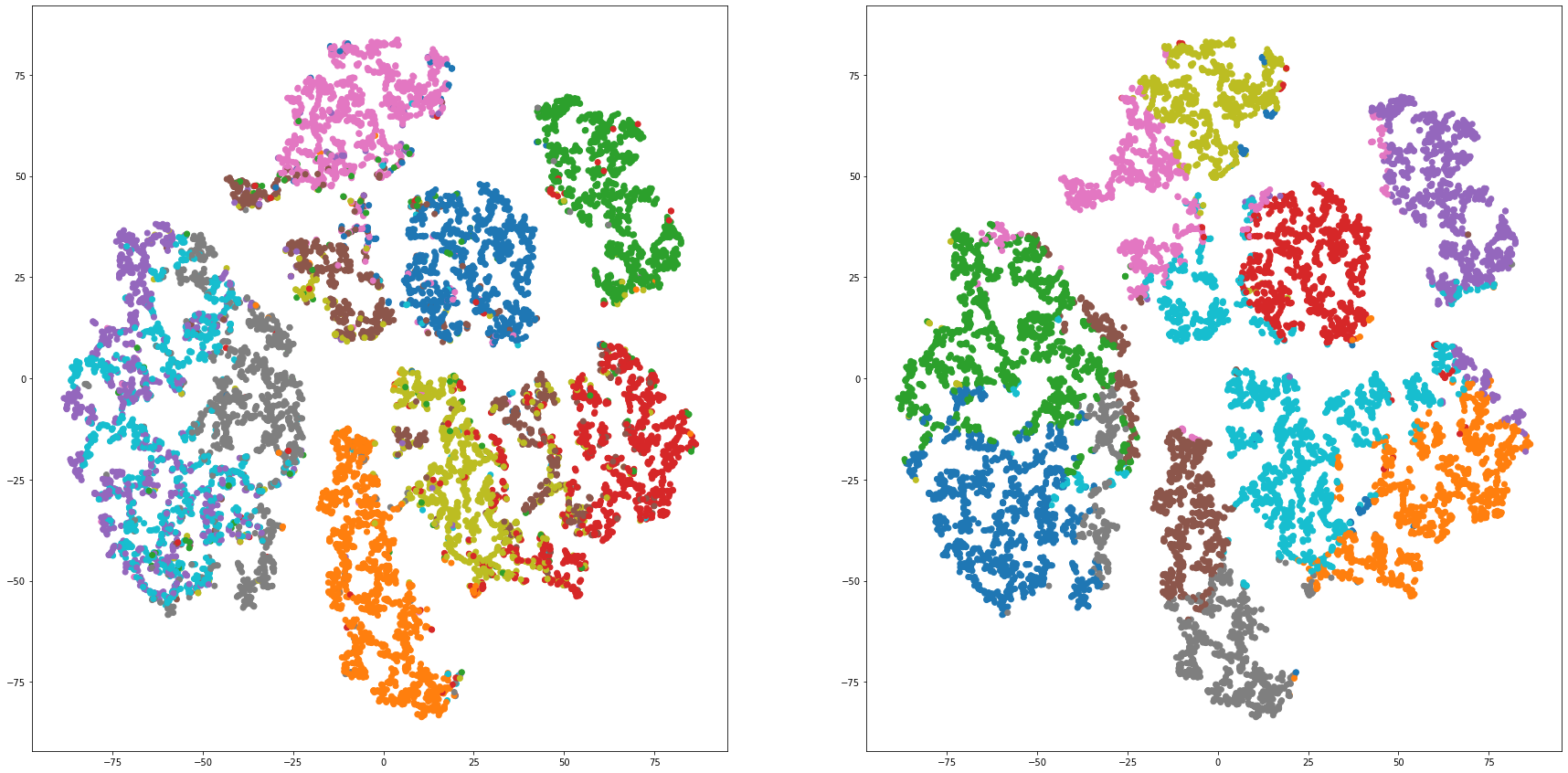
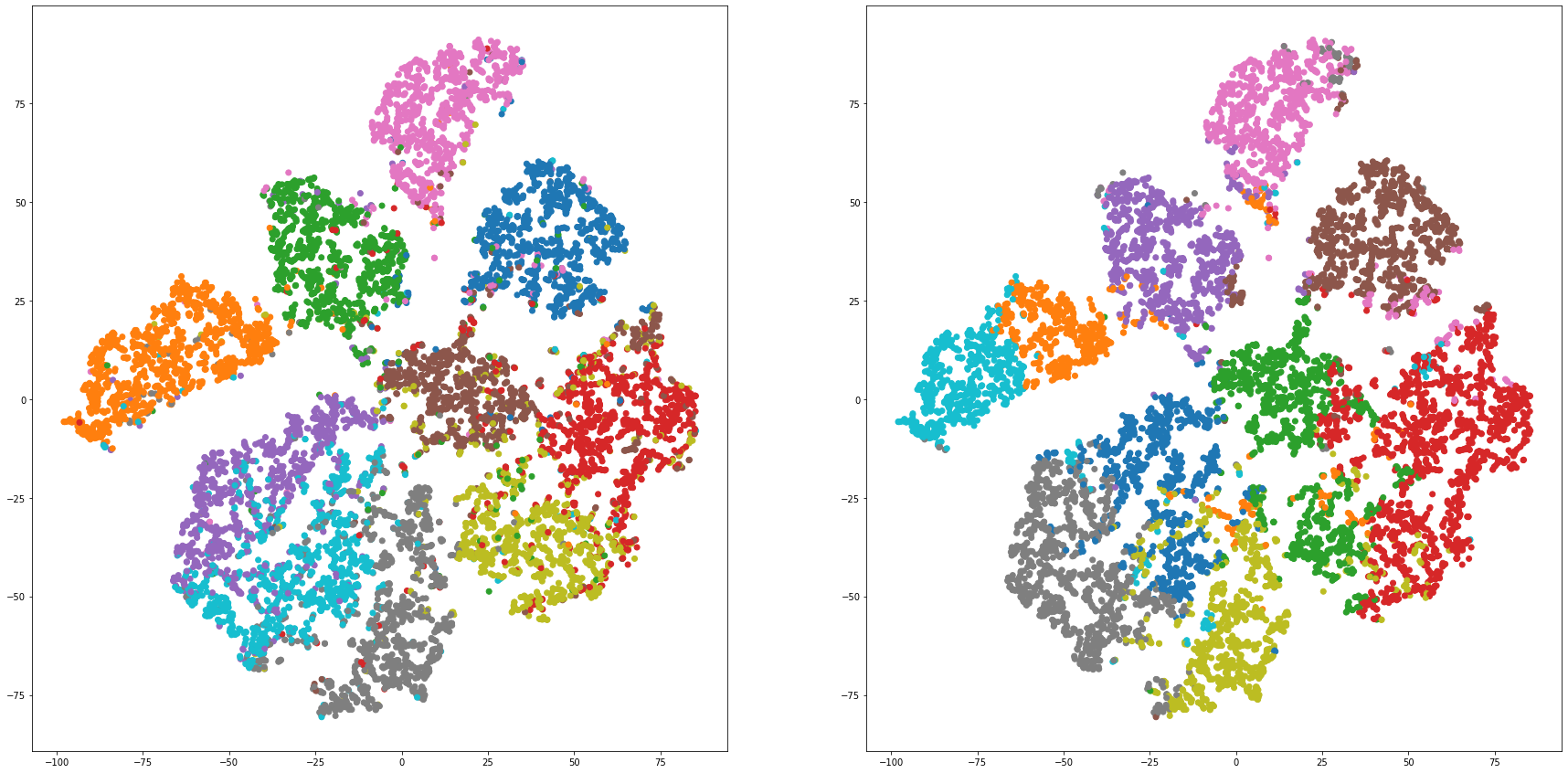

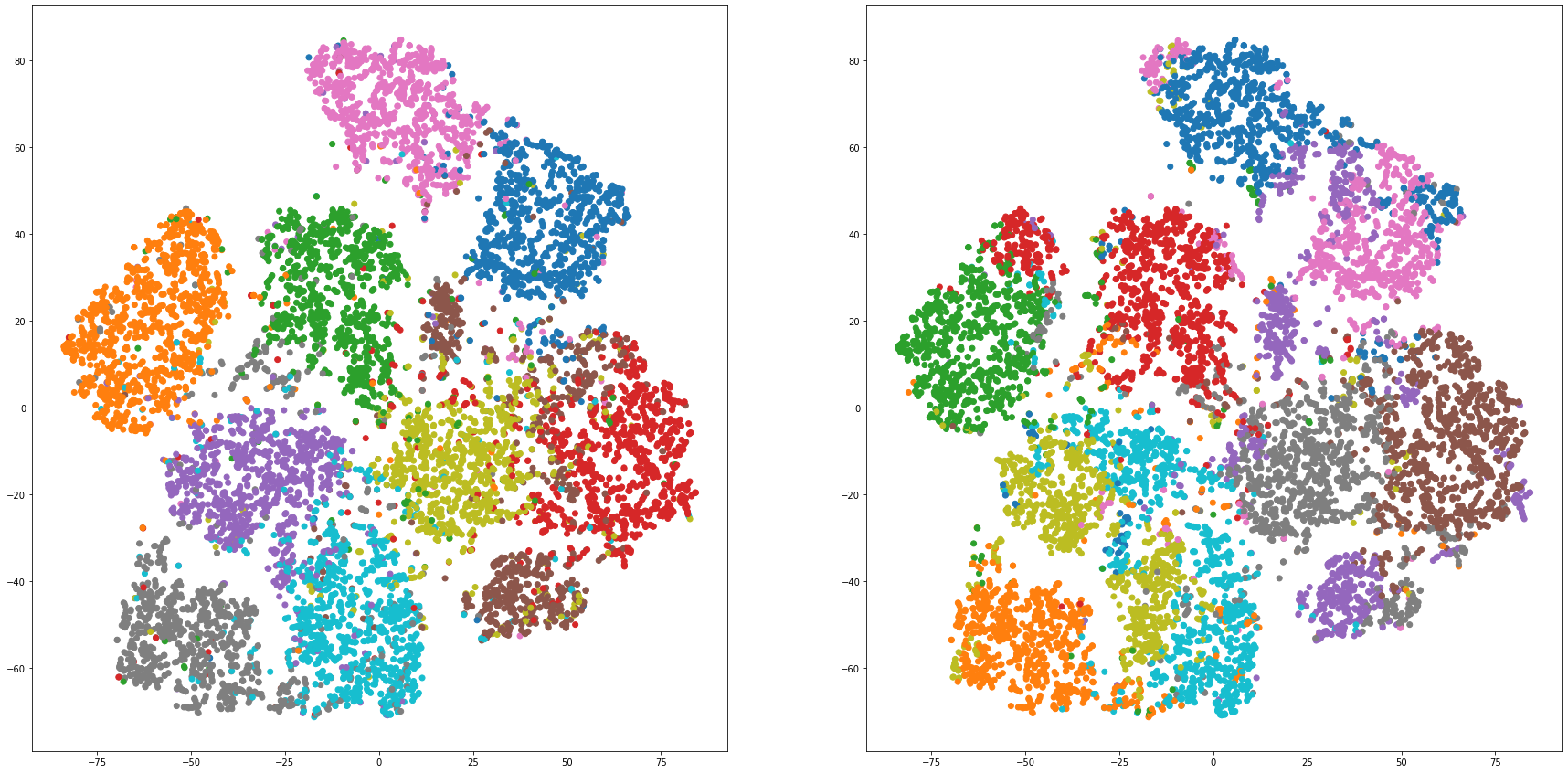
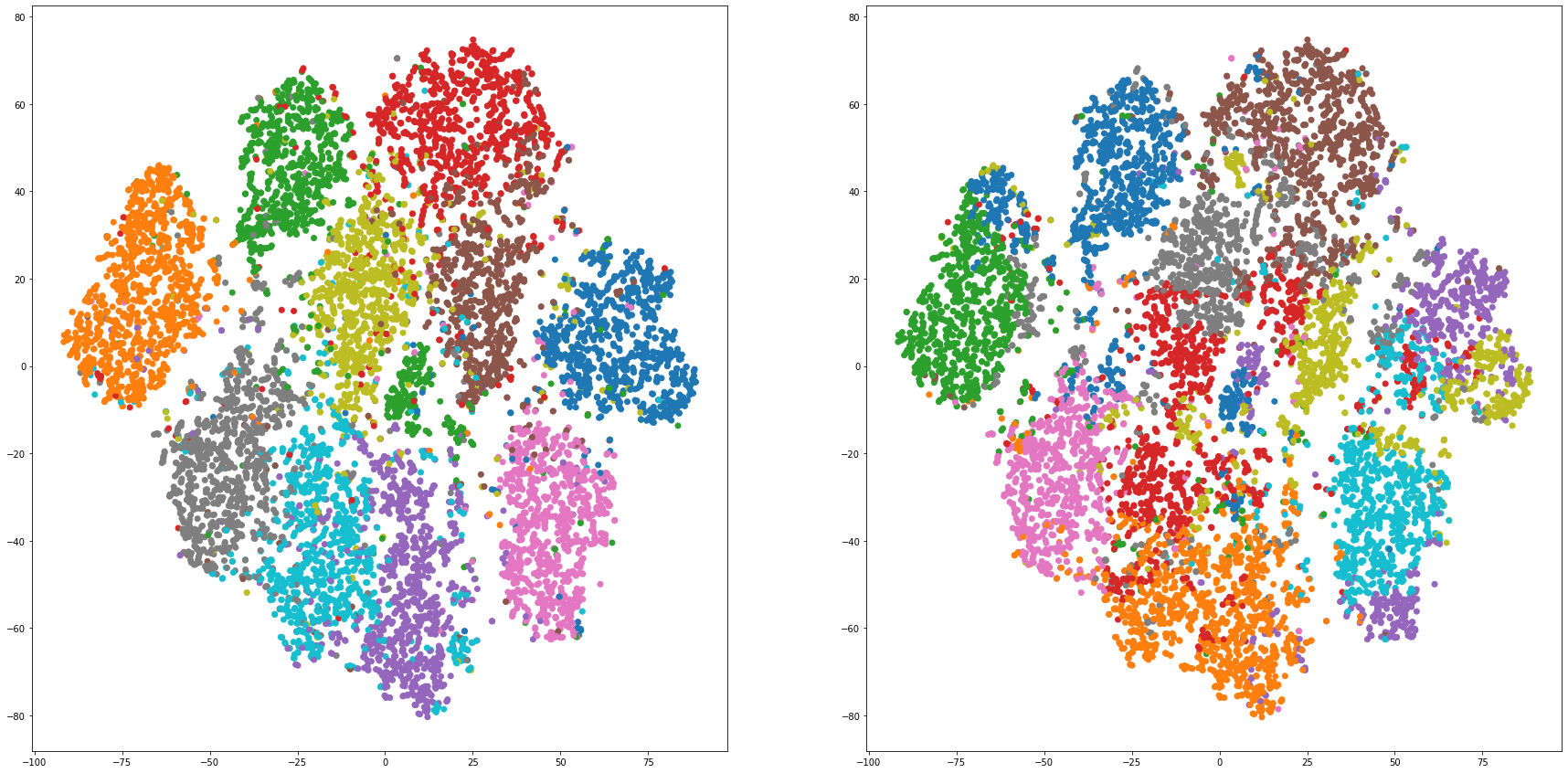

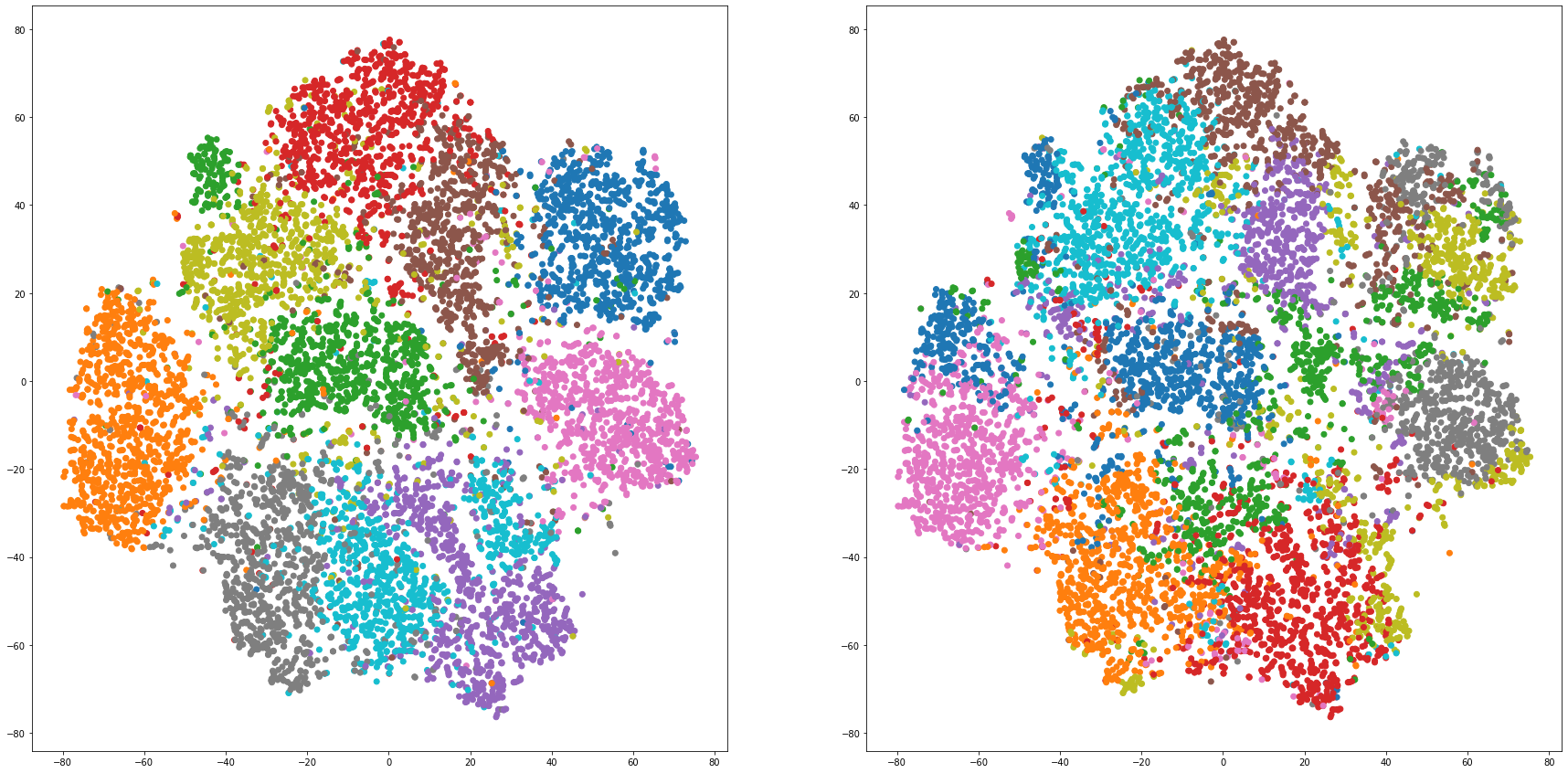
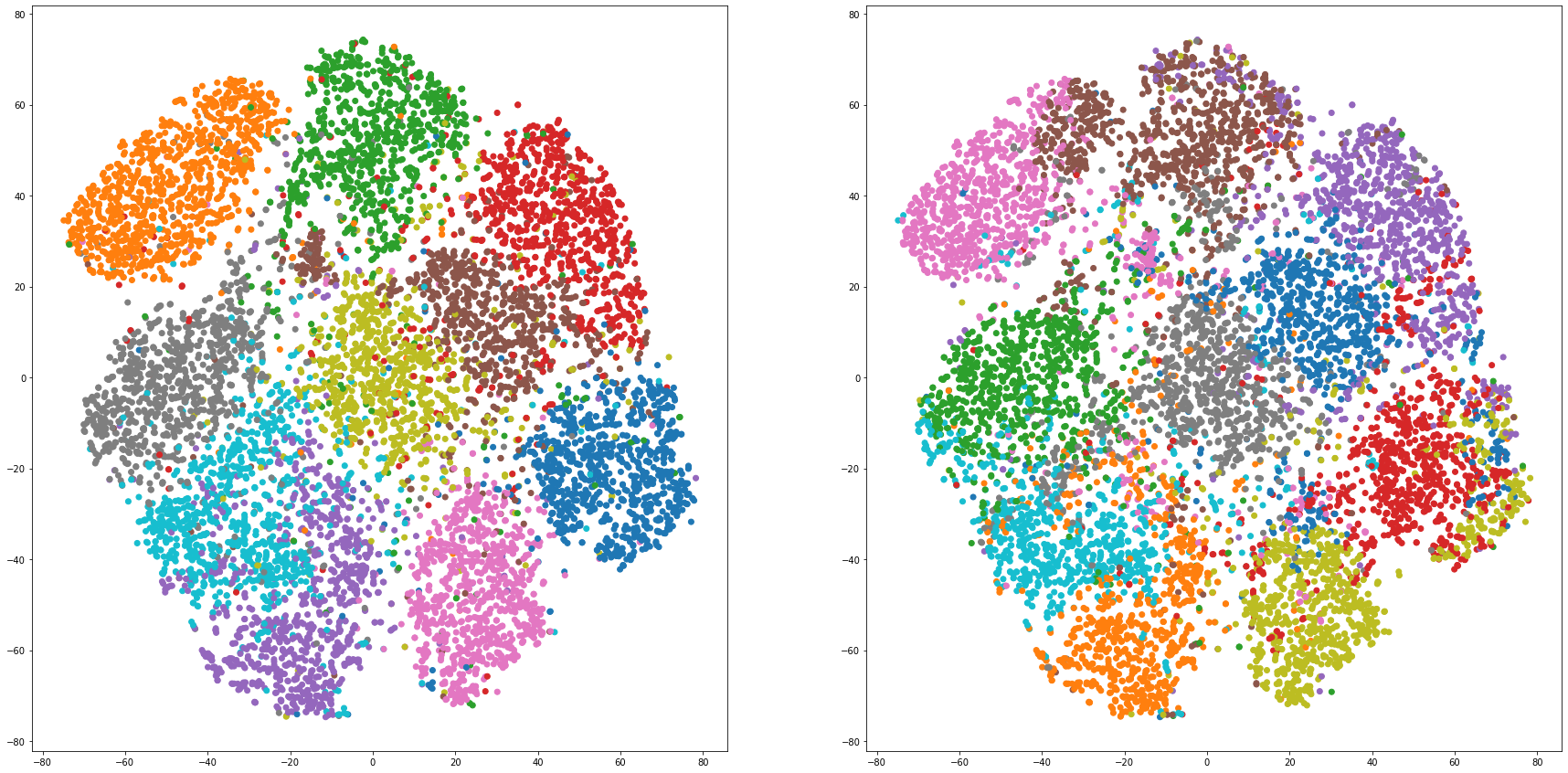

# https://qiita.com/mamika311/items/75c24f6892f85593f7e7
from sklearn.metrics.cluster import adjusted_rand_score
for i in range(len(feature_dims)):
print("dim:" + str(feature_dims[i]) + " RMI: " + str(adjusted_rand_score(labels, kms[i])))
dim:2 RMI: 0.36620498031529986
dim:3 RMI: 0.41914836520424376
dim:4 RMI: 0.49394921137719777
dim:5 RMI: 0.5245649990462847
dim:6 RMI: 0.47705674510916446
dim:7 RMI: 0.41013993209378174
dim:8 RMI: 0.3698302406743967
dim:9 RMI: 0.32840225806718926
dim:10 RMI: 0.4466812382927318
dim:11 RMI: 0.4090677997413063
# https://scikit-learn.org/stable/modules/generated/sklearn.metrics.normalized_mutual_info_score.html
# https://qiita.com/kotap15/items/38289edfe822005e1e44
from sklearn.metrics import normalized_mutual_info_score
#display(normalized_mutual_info_score(labels, df['km']))
for i in range(len(feature_dims)):
print("dim:" + str(feature_dims[i]) + " NMI: " + str(normalized_mutual_info_score(labels, kms[i])))
dim:2 NMI: 0.5199419992579754
dim:3 NMI: 0.56100353575167
dim:4 NMI: 0.605060303081276
dim:5 NMI: 0.6020900415664949
dim:6 NMI: 0.5631744057166579
dim:7 NMI: 0.5014462787979749
dim:8 NMI: 0.46110014862882315
dim:9 NMI: 0.42836636346088663
dim:10 NMI: 0.5187118150024308
dim:11 NMI: 0.48519256224162205
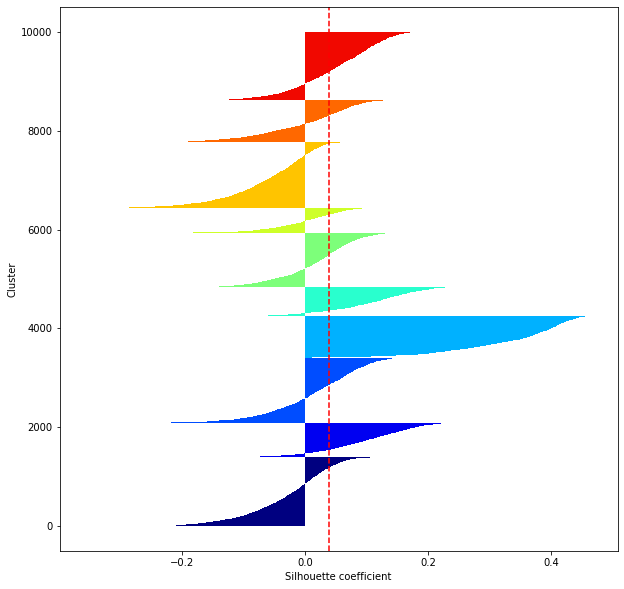
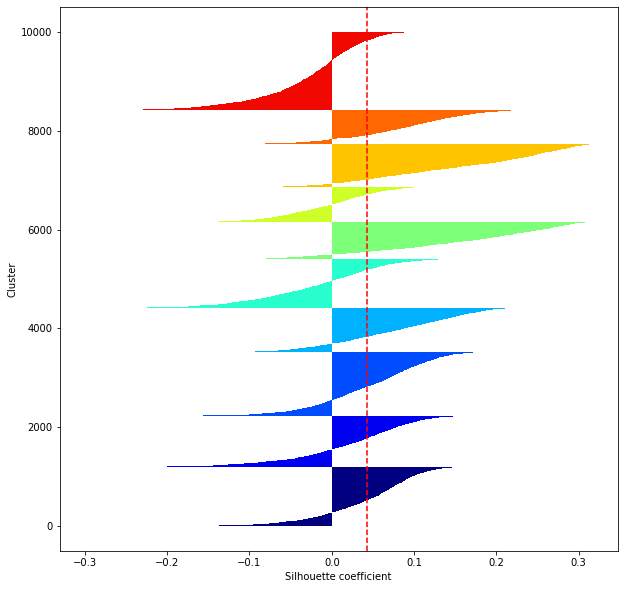
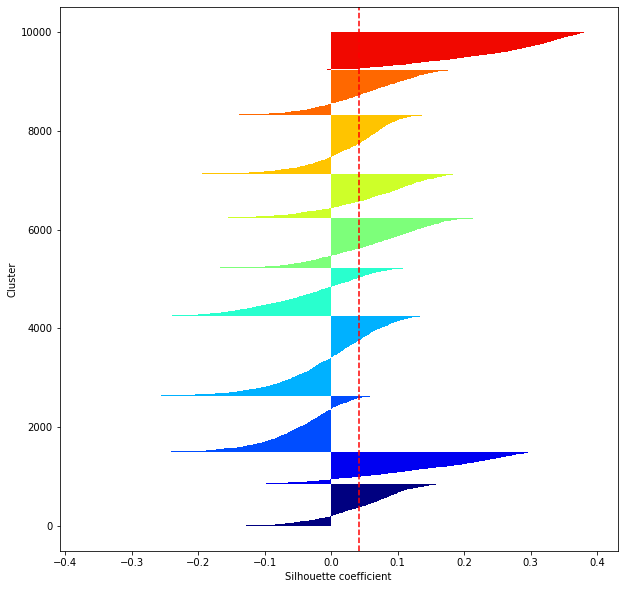
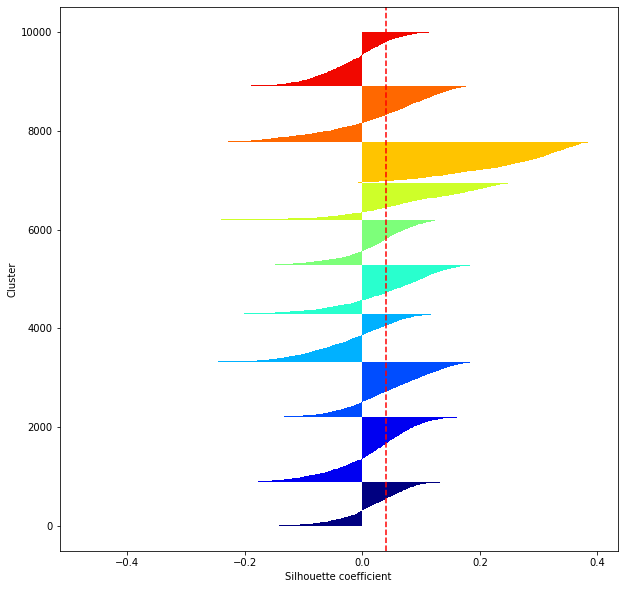
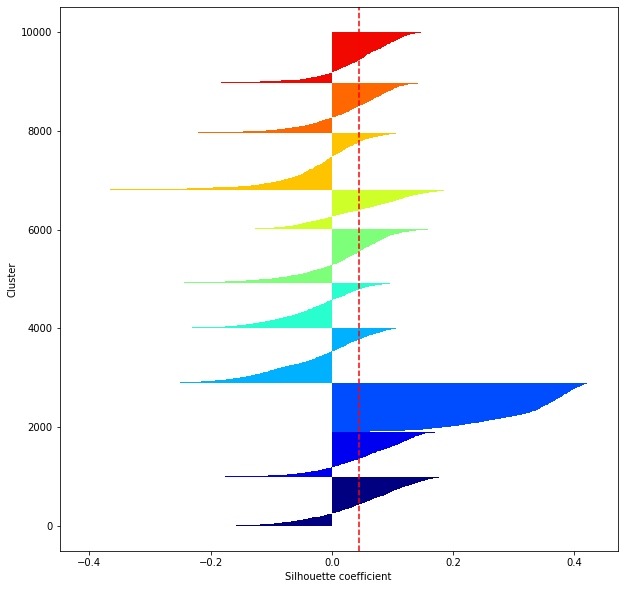
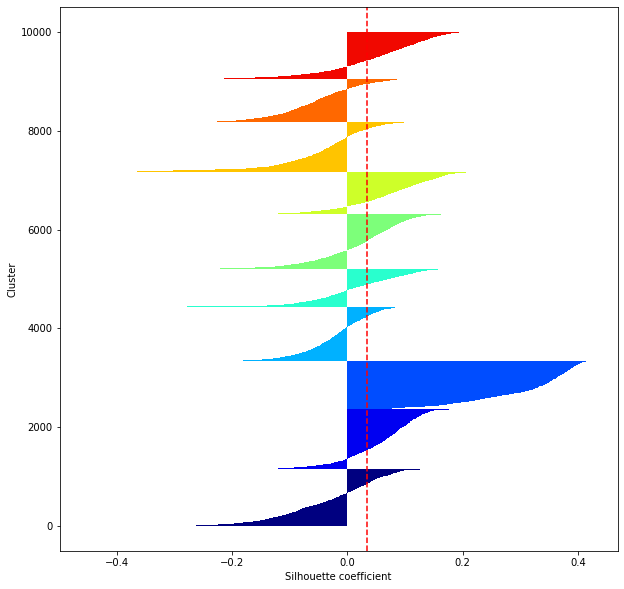
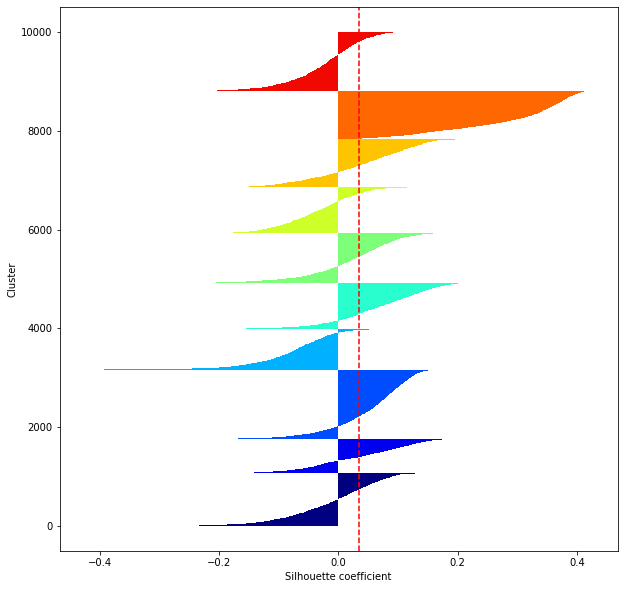
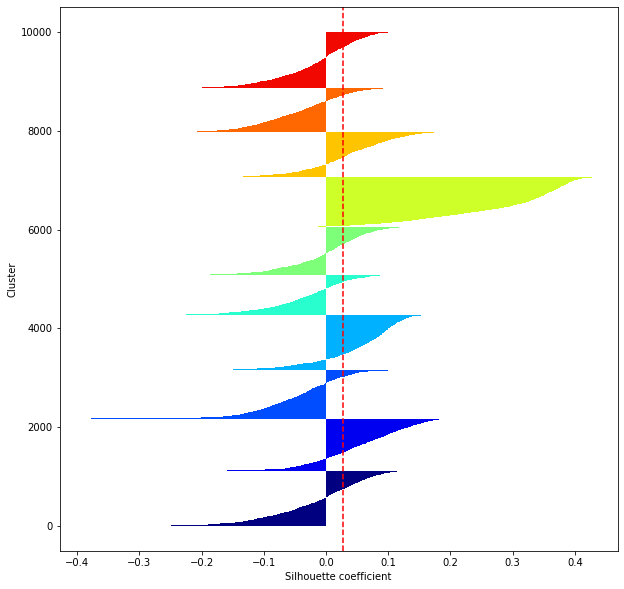
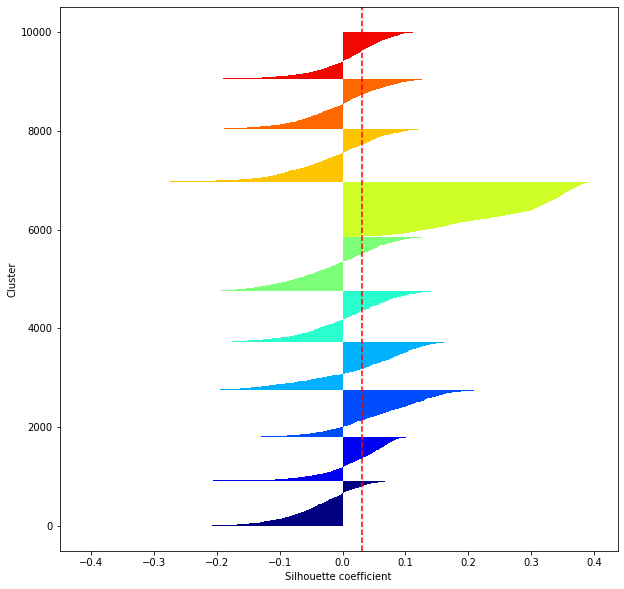
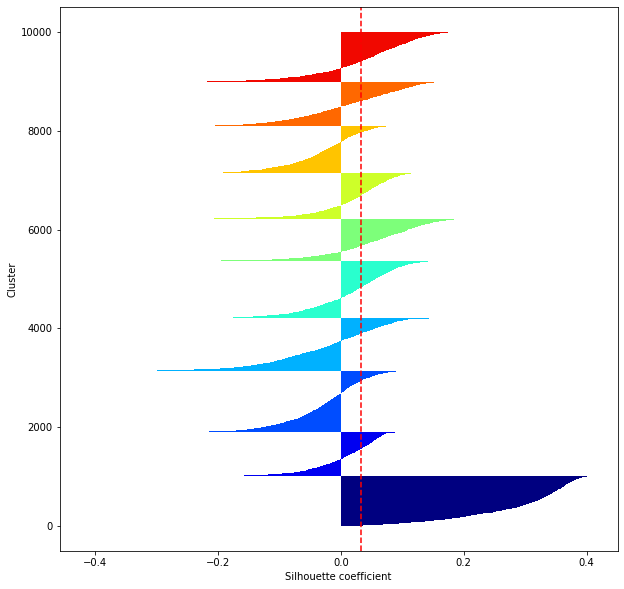
def shilhouette(clusters, x_test):
from sklearn.metrics import silhouette_samples
from matplotlib import cm
plt.figure(figsize = (10, 10))
cluster_labels=np.unique(clusters)
n_clusters=cluster_labels.shape[0]
silhouette_vals=silhouette_samples(x_test,clusters,metric='euclidean')
y_ax_lower,y_ax_upper=0,0
yticks=[]
for i,c in enumerate(cluster_labels):
c_silhouette_vals=silhouette_vals[clusters==c]
print(len(c_silhouette_vals))
c_silhouette_vals.sort()
y_ax_upper +=len(c_silhouette_vals)
color=cm.jet(float(i)/n_clusters)
plt.barh(range(y_ax_lower,y_ax_upper),
c_silhouette_vals,
height=1.0,
edgecolor='none',
color=color
)
yticks.append((y_ax_lower+y_ax_upper)/2.)
y_ax_lower += len(c_silhouette_vals)
#Si le coefficient de silhouette est 1, vous pouvez bien regrouper.
#De plus, lorsque la largeur de la silhouette est égale en moyenne en termes de nombre de clusters, cela indique que l'ensemble des données peut être divisé également.
#Cette largeur de division=Une méthode de réglage possible consiste à optimiser k de sorte que les largeurs des barres de silhouette soient égales et que le coefficient de silhouette se rapproche de 1..
#Tracez une ligne à la position moyenne
silhouette_avg=np.mean(silhouette_vals)
plt.axvline(silhouette_avg,color="red",linestyle="--")
plt.ylabel("Cluster")
plt.xlabel("Silhouette coefficient")
for i in range(len(feature_dims)):
shilhouette(kms[i], x_test)
1391
704
1316
843
582
1102
500
1330
848
1384
1196
1035
1287
901
976
751
718
859
695
1582
852
657
1130
1615
977
994
904
1186
914
771
883
1316
1130
964
982
928
737
829
1140
1091
997
898
1000
1122
911
1078
803
1152
998
1041
1149
1211
976
1106
765
1100
852
1010
886
945
1070
696
1395
825
934
1008
926
969
981
1196
1117
1060
975
1118
807
970
1007
922
881
1143
921
878
948
971
1033
1098
1109
1077
1013
952
1008
888
1248
1059
1166
848
925
961
889
1008
Recommended Posts