Créer un graphique de distribution normale standard en Python
1. Qu'est-ce que la distribution normale standard?
Distribution normale avec moyenne μ = 0, variance σ = 1, Autrement dit, il s'agit d'une fonction exprimée par la formule suivante.
f(x) = \frac{1}{ \sqrt{2 \pi } } e^{- \frac{x^2}{2} }
2. Créez votre propre distribution normale standard
Si vous définissez f (x) par vous-même et essayez de mettre [-5,0, -4,999, -4,998, ..., 4,998, 4,999, 5,0] et une séquence de ~ 5,0 ~ 5,0, Vous obtiendrez un graphique qui est communément appelé une distribution normale.
norm_original.py
# coding: utf-8
import numpy as np
import math
# f(x)Écrivez par vous-même
f = lambda x: (math.exp(-x**2/2)) / math.sqrt(2*math.pi)
#Vecteur x[-5.0, ..., 5.0]Créé dans la section de
n = np.linspace(-5.0, 5.0, 10000)
# f(x)Obtenez le résultat de
p = []
for i in range(len(n)):
p.append(f(n[i]))
#Affichage sur graphique
plt.scatter(n, p)
plt.show()

J'ai une belle cloche, mais c'est un peu ennuyeux de la définir une à une. Surtout, il faut du temps pour changer la moyenne ou la variance.
3. Utilisez scipy
Avec le module scipy.stats Dans le code ci-dessus (norm_original.py), la formule définie par l'expression lambda peut être appelée à partir de la fonction.
norm_usescipy.py
# coding: utf-8
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
#Vecteur x[-5.0, ..., 5.0]Créé dans la section de
n = np.linspace(-5.0, 5.0, 10000)
#Moyenne 0,Trouvez la probabilité de x dans une distribution normale avec un écart type de 1.
p = []
for i in range(len(n)):
p.append(norm.pdf(x=n[i], loc=0, scale=1))
#Créez un graphique de distribution normale standard en montrant les caractéristiques de la probabilité de nombre aléatoire dans un diagramme de dispersion.
plt.scatter(n, p)
plt.show()
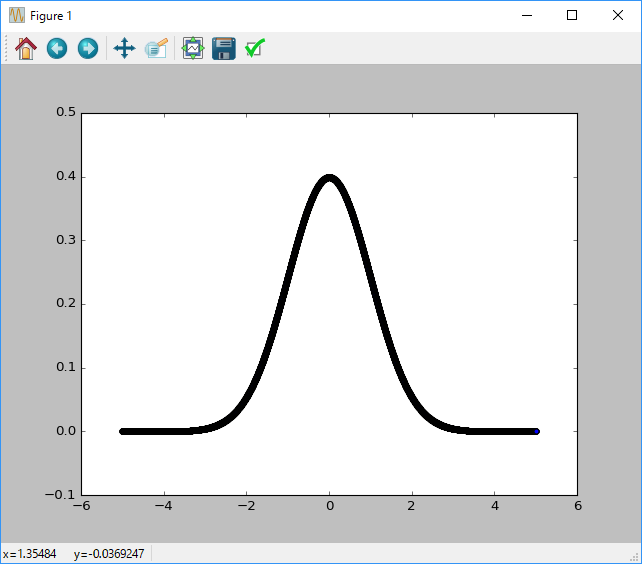
Puisque vous pouvez spécifier la moyenne et la variance avec l'argument, vous pouvez facilement obtenir une distribution normale avec une forme différente.
4. Regardons l'entropie simultanée de la fonction de distribution cumulative
Dans le chapitre précédent, nous avons utilisé la fonction de densité de probabilité normalement distribuée de scipy.stats.norm.pdf. Jouons maintenant un peu avec et utilisons la fonction de distribution cumulative de la distribution normale de scipy.stats.norm.cdf.
Entropie combinée de Wikipedia (https://ja.wikipedia.org/wiki/%E7%B5%90%E5%90%88%E3%82%A8%E3%83%B3%E3%83%88% E3% 83% AD% E3% 83% 94% E3% 83% BC) Je vais l'écrire en me référant à la description.
L'entropie simultanée (entropie combinée) H (X) représente l'incertitude de la valeur de la variable stochastique X. Lorsque la probabilité que l'événement x appartenant à X se produise est p (x), l'entropie de X est
H(X) = - \sum_{x} p_x log_2 (p_x)
Il est représenté par.
Ici, en supposant que la probabilité est sur la distribution normale standard, si l'entropie est représentée dans un graphe,
norm_usescipy.py
---p.append(norm.pdf(x=n[i], loc=0, scale=1))
+++p.append(norm.cdf(x=n[i], loc=0, scale=1))

Vous pouvez obtenir H (X) comme ça.
Recommended Posts