Traitement du signal acoustique avec Python

Ceci est l'article sur le 13e jour du Calendrier de l'Avent Python Partie 2 2015. Mon travail habituel consiste principalement à développer des algorithmes pour le traitement du signal acoustique et à implémenter des DSP, mais lors de la construction d'un algorithme, j'examine d'abord l'algorithme en utilisant Python, et en fonction des résultats, C et C ++ Le flux consiste à créer un modèle en temps réel qui s'exécute sur un PC. Étonnamment, il n'y a pas d'article japonais complet sur le traitement du signal acoustique, je voudrais donc résumer ici de manière appropriée la méthode de traitement du signal acoustique en Python et le savoir-faire que j'ai utilisé dans mon travail jusqu'à présent.

table des matières

• Motivation pour traiter les signaux acoustiques avec Python
• Lecture et écriture de fichiers audio
• Je souhaite effectuer un traitement audio en temps réel
• Je veux afficher la réponse en fréquence
• Je souhaite concevoir un filtre numérique
• Je veux convertir des zéros, des pôles et des tableaux de coefficients b, a
• Je souhaite appliquer un filtre numérique à un signal de série chronologique
• Je veux calculer le délai de groupe
• Je veux calculer la corrélation temporelle (fonction de corrélation mutuelle)
• Je veux détecter un pic

Motivation à traiter les signaux acoustiques avec Python

Une alternative à matlab. Pour être honnête, le matlab est traité comme une immobilisation fixe car il coûte plus de 200000 pour un usage commercial, et il est difficile à gérer ou l'entreprise ne peut pas l'acheter en premier lieu, alors je veux faire quelque chose gratuitement.

Lire et écrire des fichiers audio

Pour plus d'informations sur la lecture et l'écriture de fichiers audio, consultez l'article 108 façons de gérer les fichiers wav avec python que j'ai écrit sur mon blog dans le passé. C'est résumé. Personnellement, j'utilise plus souvent PySoundFile ces jours-ci. Ce qui suit est un processus qui ne contient que des FFT avec un chevauchement de 1/2, des IFFT et des restaurations.

#!/usr/bin/env python
# vim:fileencoding=utf-8

import sys

import numpy as np
import scipy.fftpack as fft
import matplotlib.pyplot as plt

import soundfile as sf

if __name__ == '__main__':
    plt.close("all")

    #Lire le fichier wav
    filename = sys.argv[1]
    wav, fs = sf.read(filename)

    #Dans le cas de la stéréo 2ch, il est divisé en Lch et Rch
    wav_l = wav[:, 0]
    wav_r = wav[:, 1]

    #Entrée monophonique
    xs = (0.5 * wav_l) + (0.5 * wav_r)

    n_len = len(xs)
    n_fft = 128
    n_overlap = 2
    n_shift = n_fft / n_overlap

    #Tampon intermédiaire
    zs = np.zeros(n_len)
    Zs = np.zeros(n_fft)

    #Tampon de sortie
    ys = np.zeros(n_len)

    #Fonction de fenêtre
    window = np.hanning(n_fft)

    # FFT & IFFT
    for start in range(0, n_len - n_shift, n_shift):
        xs_cut = xs[start: start + n_fft]
        xs_win = xs_cut * window
        Xs = fft.fft(xs_win, n_fft)

        # some signal processing
        Zs = Xs
        zs = fft.ifft(Zs, n_fft)

        # write output buffer
        ys[start: start + n_fft] += np.real(zs)

    #10 secondes de tracé depuis le début
    fig = plt.figure(1, figsize=(8, 10))
    ax = fig.add_subplot(211)
    ax.plot(xs[:fs*10])
    ax.set_title("input signal")
    ax.set_xlabel("time [pt]")
    ax.set_ylabel("amplitude")

    ax = fig.add_subplot(212)
    ax.plot(ys[:fs*10])
    ax.set_title("output signal")
    ax.set_xlabel("time [pt]")
    ax.set_ylabel("amplitude")

    plt.show()

Exemple de tracé

Je souhaite effectuer un traitement audio en temps réel

Il est facile d'utiliser la liaison Python de PortAudio PyAudio.

Voici un exemple de mise en mémoire tampon du signal d'entrée du microphone dans une variable globale dans la méthode de rappel et de son enregistrement dans un fichier wav. Commencez par répertorier les appareils disponibles.

pyaudio_print_devices.py

#!/usr/bin/env python
# vim:fileencoding=utf-8

import pyaudio as pa

if __name__ == "__main__":
    #Liste des appareils disponibles
    p_in = pa.PyAudio()
    print "device num: {0}".format(p_in.get_device_count())
    for i in range(p_in.get_device_count()):
        print p_in.get_device_info_by_index(i)

$ python pyaudio_print_devices.py
device num: 2
{'defaultSampleRate': 44100.0, 'defaultLowOutputLatency': 0.01, 'defaultLowInputLatency': 0.00199546485260771, 'maxInputChannels': 2L, 'structVersion': 2L, 'hostApi': 0L, 'index': 0, 'defaultHighOutputLatency': 0.1, 'maxOutputChannels': 0L, 'name': u'Built-in Microph', 'defaultHighInputLatency': 0.012154195011337868}
{'defaultSampleRate': 44100.0, 'defaultLowOutputLatency': 0.004693877551020408, 'defaultLowInputLatency': 0.01, 'maxInputChannels': 0L, 'structVersion': 2L, 'hostApi': 0L, 'index': 1, 'defaultHighOutputLatency': 0.014852607709750568, 'maxOutputChannels': 2L, 'name': u'Built-in Output', 'defaultHighInputLatency': 0.1}

Si vous regardez "maxInputChannels", vous pouvez voir qu'il s'agit du périphérique d'entrée car le premier périphérique est 2L et le "nom" est u'Built-in Microph '.

Vient ensuite un script qui enregistre l'entrée du microphone dans un fichier wav. PyAudio possède une méthode de traitement non bloquante qui utilise un rappel et une méthode de traitement bloquant qui n'utilise pas de rappel. Ici, l'ancienne méthode qui utilise un rappel est utilisée pour le traitement. Dans la méthode de rappel, le signal d'entrée est converti de court à un flottant de -1,0 à 1,0, et il est simplement combiné avec la variable globale xs.

#!/usr/bin/env python
# vim:fileencoding=utf-8

import time

import numpy as np

import soundfile as sf
import pyaudio as pa


# global
xs = np.array([])


def callback(in_data, frame_count, time_info, status):
    global xs
    in_float = np.frombuffer(in_data, dtype=np.int16).astype(np.float)
    in_float[in_float > 0.0] /= float(2**15 - 1)
    in_float[in_float <= 0.0] /= float(2**15)
    xs = np.r_[xs, in_float]

    return (in_data, pa.paContinue)

if __name__ == "__main__":
    # pyaudio
    p_in = pa.PyAudio()
    py_format = p_in.get_format_from_width(2)
    fs = 16000
    channels = 1
    chunk = 1024
    use_device_index = 0

    #Créer un flux d'entrée
    in_stream = p_in.open(format=py_format,
                          channels=channels,
                          rate=fs,
                          input=True,
                          frames_per_buffer=chunk,
                          input_device_index=use_device_index,
                          stream_callback=callback)

    in_stream.start_stream()

    # input loop
    #Entrez quelque chose et terminez
    while in_stream.is_active():
        c = raw_input()
        if c:
            break
        time.sleep(0.1)
    else:
        in_stream.stop_stream()
        in_stream.close()

    #Enregistrer le signal d'entrée
    sf.write("./pyaudio_output.wav", xs, fs)

    p_in.terminate()

Faites ceci et tapez quelque chose pour sortir de la boucle while et enregistrer xs dans "./pyaudio_output.wav". Si vous définissez output = True au lieu de input = True lors de l'ouverture de p_in, il sera traité comme un périphérique de lecture. Pour plus de détails, consultez l'exemple au bas de la page PyAudio.

Je souhaite afficher la réponse en fréquence

scipy.signal a une méthode pour trouver la réponse en fréquence appelée freqz. Comme je l'ai écrit dans Article, la partie où le polynôme est calculé par np.polyval est lourde, et elle est lente lorsqu'elle est exécutée en continu. Cela se démarque vraiment. Par conséquent, comme je l'ai écrit dans l'article précédent, vous pouvez trouver la réponse en fréquence en définissant la méthode suivante qui utilise scipy.fftpack.

def my_freqz(b, a=[1], worN=None):
    import scipy.fftpack as fft
    lastpoint = np.pi
    N = 512 if worN is None else worN
    w = np.linspace(0.0, lastpoint, N, endpoint=False)
    h = fft.fft(b, 2 * N)[:N+1] / fft.fft(a, 2 * N)[:N+1]
    return w, h

Par exemple, supposons que vous vouliez la réponse d'un simple filtre d'amélioration b = [1,0, -0,97] et d'un filtre de-enfasis b = [1,0], a = [1,0, -0,97] qui restaure ses caractéristiques. Vous pouvez tracer chaque réponse en fréquence avec un script comme celui-ci: Notez que l'axe horizontal lors du traçage va de 0 à FS / 2 car la plage de w est de 0 à π.

#!/usr/bin/env python
# vim:fileencoding=utf-8

import numpy as np
import matplotlib.pyplot as plt


def my_freqz(b, a=[1], worN=None):
    import scipy.fftpack as fft
    lastpoint = np.pi
    N = 512 if worN is None else worN
    w = np.linspace(0.0, lastpoint, N, endpoint=False)
    h = fft.fft(b, 2 * N)[:N] / fft.fft(a, 2 * N)[:N]
    return w, h

if __name__ == "__main__":
    plt.close("all")

    N = 1024
    FS = 16000.0
    EMP = -0.97

    b_emp = [1.0, EMP]
    a_emp = [1.0]

    b_deemp = [1.0]
    a_deemp = [1.0, EMP]

    (w_emp, h_emp) = my_freqz(b_emp, a_emp, worN=N)
    (w_deemp, h_deemp) = my_freqz(b_deemp, a_deemp, worN=N)

    fig = plt.figure(1)

    ax = fig.add_subplot(2, 1, 1)
    ax.semilogx(w_emp * (FS / 2.0) / np.pi,
                20.0 * np.log10(np.abs(h_emp)))
    ax.grid()
    ax.set_xlabel("frequency response [Hz]")
    ax.set_ylabel("power [dB]")

    ax = fig.add_subplot(2, 1, 2)
    ax.semilogx(w_deemp * (FS / 2.0) / np.pi,
                20.0 * np.log10(np.abs(h_deemp)))
    ax.grid()
    ax.set_xlabel("frequency response [Hz]")
    ax.set_ylabel("power [dB]")

    plt.show()

Cela tracera une réponse similaire à celle ci-dessous.

Je souhaite concevoir un filtre numérique

Diverses fonctions de conception de filtre sont fournies dans scipy.signal, y compris les fonctions de conception de filtre FIR (firwin, firwin2, remez, etc.) et les fonctions de conception IIR compatibles matlab (butter, buttord, cheby1, cheb1ord, etc.) ..

Par exemple, pour rechercher LPF, BPF, HPF à l'aide de firwin, vous pouvez utiliser le script suivant.

#!/usr/bin/env python
# vim:fileencoding=utf-8

import numpy as np
import matplotlib.pyplot as plt
import scipy.signal as sg


def my_freqz(b, a=[1], worN=None):
    import scipy.fftpack as fft
    lastpoint = np.pi
    N = 512 if worN is None else worN
    w = np.linspace(0.0, lastpoint, N, endpoint=False)
    h = fft.fft(b, 2 * N)[:N] / fft.fft(a, 2 * N)[:N]
    return w, h

if __name__ == '__main__':
    plt.close("all")

    fs = 48000.0

    num_tap = 1024
    lpf_cutoff_hz = 400.0
    hpf_cutoff_hz = 1000.0

    lpf_cutoff = lpf_cutoff_hz / (fs/2.0)
    bpf_band = np.array([lpf_cutoff_hz, hpf_cutoff_hz]) / (fs/2.0)
    hpf_cutoff = hpf_cutoff_hz / (fs/2.0)

    win = "hann"

    lpf = sg.firwin(num_tap, lpf_cutoff, window=win)
    bpf = sg.firwin(num_tap, bpf_band, pass_zero=False, window=win)
    hpf = sg.firwin(num_tap, [hpf_cutoff, 0.9999], pass_zero=False, window=win)

    # plot filter response
    w, lpf_h = my_freqz(lpf, worN=num_tap)
    w, bpf_h = my_freqz(bpf, worN=num_tap)
    w, hpf_h = my_freqz(hpf, worN=num_tap)

    lpf_amp = np.abs(lpf_h)
    bpf_amp = np.abs(bpf_h)
    hpf_amp = np.abs(hpf_h)

    fig = plt.figure(1)
    ax = fig.add_subplot(111)
    ax.semilogx(fs * w/(2 * np.pi), 20.0*np.log10(lpf_amp), "bx-")
    ax.semilogx(fs * w/(2 * np.pi), 20.0*np.log10(bpf_amp), "yx-")
    ax.semilogx(fs * w/(2 * np.pi), 20.0*np.log10(hpf_amp), "rx-")
    ax.set_xlim([0.0, 24000.0])
    ax.set_ylim([-150.0, 10.0])
    ax.set_ylabel("power [dB]")
    ax.set_xlabel("frequency [Hz]")
    ax.grid()
    ax.legend(["lpf", "bpf", "hpf"], loc="best")
    plt.show()

En conséquence, le graphique ci-dessous est tracé.

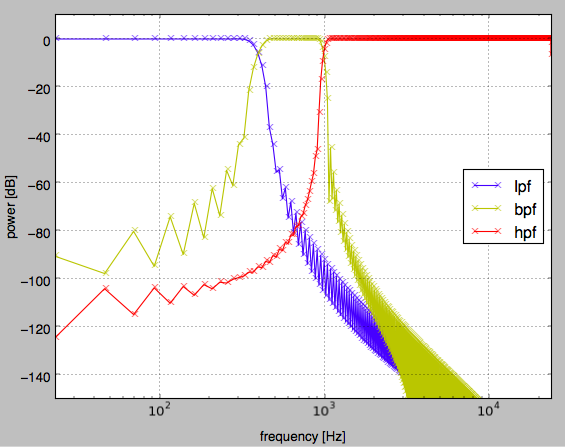
De plus, si vous souhaitez concevoir un filtre de type biquad (IIR secondaire), vous pouvez créer votre propre fonction selon EQ Cookbook. Par exemple, dans le cas d'un égaliseur de crête, cela ressemble à ce qui suit (les valeurs de retour sont b, a).

def peaking_eq(q, gain, f, fs):
    A = 10 ** (gain / 40.0)
    w0 = 2.0 * np.pi * f / fs
    alpha = np.sin(w0) / (2.0 * q)

    b = [(1.0 + alpha * A), (-2.0 * np.cos(w0)), (1.0 - alpha * A)]
    a = [(1.0 + alpha / A), (-2.0 * np.cos(w0)), (1.0 - alpha / A)]

    return (np.array(b) / a[0]), (np.array(a) / a[0])

Je veux convertir des zéros, des pôles et des tableaux de coefficients b, a

tf2zpk et zpk2tf /doc/scipy/reference/generated/scipy.signal.zpk2tf.html#scipy.signal.zpk2tf) est utilisé. tf signifie filtre temporel et zpk signifie zéro, pôle, k (gain). Si vous créez un filtre IIR de 6ème ordre, etc. et que vous le montez en C tel quel, il peut diverger en raison d'une erreur, donc si vous connaissez le point zéro et le pôle, vous pouvez décomposer le filtre en 3 étapes du filtre IIR de 2ème ordre. ..

Je souhaite appliquer un filtre numérique à un signal de série chronologique

Il existe deux manières principales d'appliquer le filtre numérique conçu à un signal de série chronologique. [Scipy.signal.lfilter](https://docs.scipy.org/doc/scipy-0.16.0/reference/generated/scipy.signal.lfilter.html#scipy.signal] pour la méthode utilisant la convolution dans le domaine temporel [scipy.signal.fftconvolve](https://docs.scipy.org/doc/scipy-0.16.0/reference/generated] pour traiter la convolution du filtre comme un processus instantané dans la région de fréquence. /scipy.signal.fftconvolve.html#scipy.signal.fftconvolve) est utilisé. Vous trouverez ci-dessous un script qui trace les résultats de l'application de lpf en entrée à l'aide de chaque méthode.

#!/usr/bin/env python
# vim:fileencoding=utf-8

import sys

import scipy.signal as sg
import matplotlib.pyplot as plt

import soundfile as sf

if __name__ == '__main__':
    plt.close("all")

    #Lire le fichier wav
    filename = sys.argv[1]
    wav, fs = sf.read(filename)

    #Dans le cas de la stéréo 2ch, il est divisé en Lch et Rch
    wav_l = wav[:, 0]
    wav_r = wav[:, 1]

    #Entrée monophonique
    xs = (0.5 * wav_l) + (0.5 * wav_r)

    #Conception LPF
    num_tap = 1024
    lpf_cutoff_hz = 400.0
    lpf_cutoff = lpf_cutoff_hz / (fs/2.0)
    win = "hann"
    lpf = sg.firwin(num_tap, lpf_cutoff, window=win)

    #Appliquer un filtre linéaire
    ys = sg.lfilter(lpf, [1.0], xs)

    #Application de filtre de région de fréquence
    zs = sg.fftconvolve(xs, lpf, mode="same")

    #10 secondes de tracé depuis le début
    fig = plt.figure(1)
    ax = fig.add_subplot(311)
    ax.plot(xs[:fs*10])
    ax.set_title("input signal")
    ax.set_xlabel("time [pt]")
    ax.set_ylabel("amplitude")

    ax = fig.add_subplot(312)
    ax.plot(ys[:fs*10])
    ax.set_title("lfilter output signal")
    ax.set_xlabel("time [pt]")
    ax.set_ylabel("amplitude")

    ax = fig.add_subplot(313)
    ax.plot(ys[:fs*10])
    ax.set_title("fftconvolve output signal")
    ax.set_xlabel("time [pt]")
    ax.set_ylabel("amplitude")

    fig.set_tight_layout(True)

    plt.show()

Je veux calculer le délai de groupe

Quand on regarde les caractéristiques d'un filtre passe-tout, qui est un filtre qui ne change que la phase sans changer l'amplitude, en particulier, en trouvant le [group delay](https://ja.wikipedia.org/wiki/ group delay and phase delay), chaque fréquence Vous pouvez voir le délai de l'unité d'échantillonnage. Cependant, scipy.signal n'a pas la fonction grpdelay qui existe dans matlab, vous devez donc implémenter grpdelay par vous-même de manière appropriée. Par conséquent, nous allons introduire ici une méthode pour obtenir la différenciation de chaque fréquence par approximation basée sur la différence du premier ordre.

def grpdelay(w, h, fs):
    """Calcul des caractéristiques de retard de groupe par simple approximation du premier ordre(Les résultats sont des unités d'échantillonnage).. Puisqu'elle est calculée par la différence, la dimension est réduite de un, de sorte que le dernier élément est toujours défini sur 0. w est la fréquence normalisée et h est la caractéristique de fréquence correspondant à w"""
    return -1.0 * np.r_[np.diff(np.unwrap(np.angle(h))) / np.diff(w), [0]]

Ce n'est pas exactement l'algorithme utilisé dans le grpdelay de matlab, mais c'est suffisant si vous voulez juste voir les résultats approximatifs.

Je veux calculer la corrélation temporelle (fonction de corrélation mutuelle)

scipy.signal n'a pas xcorr comme on l'appelle dans matlab. Puisque xcorr trouve le spectre croisé sur la région de fréquence sur la base du théorème de Wiener Hintin et trouve la fonction d'intercorrélation par transformation inverse, il peut trouver la fonction d'intercorrélation plus rapidement que le calcul de la somme des produits dans la région temporelle.

Ce qui suit définit la méthode xcorr correspondant à la méthode my_correlate qui trouve la fonction de corrélation mutuelle dans le domaine temporel. ceil2 est une méthode qui recherche une valeur d'une puissance de 2 égale ou supérieure à l'argument. L'argument est converti en une chaîne de caractères de notation binaire, la valeur autre que le bit le plus significatif est mise à 0 dans le traitement de la chaîne de caractères et la valeur obtenue en décalant le nombre vers la gauche de 1 bit est obtenue.

def my_correlate(sig, ref, lag=None):
    lag = np.alen(ref) / 2 if lag is None else lag

    corrs = []

    sig_len = np.alen(sig)
    sig_norm = np.sqrt(np.dot(sig, sig))
    ref_norm = np.sqrt(np.dot(ref, ref))

    sig_expand = np.r_[np.zeros(lag), sig, np.zeros(lag)]
    center = lag

    for begin in range(center - lag, center + lag + 1):
        sig_cut = sig_expand[begin :begin + sig_len]
        corrs.append(np.dot(sig_cut, ref))

    return np.array(corrs) / (sig_norm * ref_norm)

def ceil2(x):
    new_x = 0
    if (x & (x - 1)) == 0:
        new_x = x
    else:
        bit_str = bin(x)
        head_bit = bit_str[2]
        tail_bits = bit_str[3:].replace("1", "0")
        new_bit_str = "0b" + head_bit + tail_bits
        new_x = int(new_bit_str, 2) << 1
    return new_x

def xcorr(sig, ref, lag=None):
    import scipy.fftpack as fft

    lag = 1024 if lag is None else lag

    sig_len = np.alen(sig)

    nfft = ceil2(sig_len)

    sig_norm = np.sqrt(np.dot(sig, sig))
    ref_norm = np.sqrt(np.dot(ref, ref))

    sig_ = sig / sig_norm
    ref_ = ref / ref_norm

    X = fft.fft(sig_, nfft)
    Y = fft.fft(ref_, nfft)

    # ifft to calculate correlation
    corr_p = np.real(fft.ifft(X * np.conjugate(Y), nfft))
    corr_m = np.real(fft.ifft(Y * np.conjugate(X), nfft))

    # concat
    corr = np.r_[corr_m[1:lag+1][::-1], corr_p[:lag+1]]

    return corr

En fait, lors de l'utilisation de FFT, nous devons tenir compte de l'influence de la patrouille, donc je pense qu'il y a place à l'amélioration dans ce qui précède. Référence: http://www.ikko.k.hosei.ac.jp/~matlab/xcorr.pdf

Je veux détecter le pic

scipy.signal a également une méthode appelée find_peaks_cwt, mais c'est plus pratique. Je voulais une fonction légère, j'utilise donc la méthode suivante.

def find_peaks(a, amp_thre, local_width=1, min_peak_distance=1):
    """
Le pic est détecté à partir du réseau en donnant le seuil, la largeur de la fenêtre pour déterminer le maximum / minimum et la distance minimum entre les pics.
En interne, la distance entre les pics est calculée en distinguant les pics positifs et négatifs, de sorte que des pics positifs et négatifs proches sont détectés.
    :rtype (int, float)
    :return tuple (ndarray of peak indices, ndarray of peak value)
    """
    # generate candidate indices to limit by threthold
    idxs = np.where(np.abs(a) > amp_thre)[0]

    # extend array to decide local maxima/minimum
    idxs_with_offset = idxs + local_width
    a_extend = np.r_[[a[0]] * local_width, a, [a[-1]] * local_width]

    last_pos_peak_idx = 0
    last_neg_peak_idx = 0
    result_idxs = []

    for i in idxs_with_offset:
        is_local_maximum = (a_extend[i] >= 0 and
                            a_extend[i] >= np.max(a_extend[i - local_width: i + local_width + 1]))
        is_local_minimum = (a_extend[i] <  0 and
                            a_extend[i] <= np.min(a_extend[i - local_width: i + local_width + 1]))
        if (is_local_maximum or is_local_minimum):
            if is_local_minimum:
                if i - last_pos_peak_idx > min_peak_distance:
                    result_idxs.append(i)
                    last_pos_peak_idx = i
            else:
                if i - last_neg_peak_idx > min_peak_distance:
                    result_idxs.append(i)
                    last_neg_peak_idx = i

    result_idxs = np.array(result_idxs) - local_width
    return (result_idxs, a[result_idxs])

c'est tout

J'ai l'impression d'avoir autre chose à écrire, mais c'est tout. La prochaine fois, c'est @kimihiro_n.