Bien que mal comprise en théorie, il s'agit d'une méthode d'estimation de la surface courbe à partir de points d'échantillonnage dispersés. Comme il est compatible avec l'échantillonnage super-carré latin montré dans Échantillonnage super-carré latin avec OpenMDAO (échantillonnage dispersé), CAE est techniquement utilisé. Il est souvent utilisé pour estimer la surface de réponse.
Le résumé des efforts est le suivant. Tout d'abord, lisez les données (fichier doe_paraboloid) expérimentées avec l'échantillonnage super carré latin avec OpenMDAO. Ensuite, le modèle d'approximation de Kriging est entraîné et créé à l'aide des données expérimentales lues. Enfin, la validité du modèle est confirmée en traçant les valeurs interpolées par le modèle d'approximation de Kriging créé comme une solution théorique (fil de fer) L'équation suivante est la solution théorique.
\begin{align}
& f(x,y) = (x-3)^2 + xy + (y+4)^2 - 3 \\
{\rm subject \: to} \: \: \:& -50.0\leq x \leq 50.0 \\
& -50.0\leq y \leq 50.0
\end{align}
Préparez le fichier training_mm.py suivant
training_mm.py
from __future__ import print_function
from openmdao.api import Group, MetaModel, FloatKrigingSurrogate
class TrainingMM(Group):
''' FloatKriging gives responses as floats '''
def __init__(self):
super(TrainingMM, self).__init__()
# Create meta_model for f_x as the response
mm = self.add("parabo_mm", MetaModel())
mm.add_param('x', val=0.)
mm.add_param('y', val=0.)
mm.add_output('f_xy', val=0., surrogate=FloatKrigingSurrogate())
Nous avons ajouté un composant appelé MetaModel qui entraîne un modèle approximatif et évalue sa valeur. Un modèle de substitution appelé FloatKrigingSurrogate est défini pour approximer f_xy. FloatKrigingSurrogate a seul la fonction de former le modèle approximatif et d'évaluer la valeur. La documentation officielle indique que MetaModel peut être utilisé pour entraîner plusieurs modèles approximatifs en même temps.
Préparez le kriging_paraboloid.py suivant. La première moitié est le processus de lecture des données expérimentales à l'apprentissage du modèle d'approximation de Kriging.
kriging_paraboloid.py
#! /bin/python
import pickle
import numpy as np
import sqlitedict
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from openmdao.api import Problem
from training_mm import TrainingMM
db =sqlitedict.SqliteDict("doe_paraboloid","iterations")
res = np.array([[0.,0.,0.]] * len(db.items()))
for i, v in enumerate(db.items()):
res[i,0] = v[1]["Unknowns"]["x"]
res[i,1] = v[1]["Unknowns"]["y"]
res[i,2] = v[1]["Unknowns"]["f_xy"]
prob = Problem()
prob.root = TrainingMM()
prob.setup()
prob["parabo_mm.train:x"] = res[:,0]
prob["parabo_mm.train:y"] = res[:,1]
prob["parabo_mm.train:f_xy"] = res[:,2]
prob.run()
La seconde moitié est illustrée ci-dessous. Un graphique est utilisé pour comparer le modèle d'approximation de krigeage créé avec la solution théorique.
kriging_paraboloid.py a continué
x = np.arange(-50., 50., 4.)
y = np.arange(-50., 50., 4.)
sg = prob.root.parabo_mm._init_unknowns_dict["f_xy"]["surrogate"]
f = open("./kriging_parabo","w")
pickle.dump(sg, f)
f.close()
f = open("./kriging_parabo_mm","w")
pickle.dump(prob.root.parabo_mm, f)
f.close()
xyzkrig = np.array([[xi,yi,sg.predict(np.array([xi,yi]))[0]] \
for xi in x for yi in y])
#xyzkrig = np.array([[0.,0.,0.]]*(25*25))
#cnt = 0
#for xi in x:
# for yi in y:
# xyzkrig[cnt,0] = prob["parabo_mm.x"] = xi
# xyzkrig[cnt,1] = prob["parabo_mm.y"] = yi
# prob.run()
# xyzkrig[cnt,2] = prob["parabo_mm.f_xy"]
# cnt += 1
fig = plt.figure(figsize=(6,4)); ax = Axes3D(fig)
X, Y = np.meshgrid(x, y)
Z = (X-3.0)**2. + X*Y + (Y+4.0)**2. - 3.0
ax.plot_wireframe(X,Y,Z,label="theoretical surface")
ax.scatter3D(xyzkrig[:,0], xyzkrig[:,1], xyzkrig[:,2], c="r", marker="o",label="Interpolated value")
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('f_xy')
plt.legend()
plt.show()
La première moitié de kriging_paraboloid.py est omise et seule la seconde moitié est expliquée. Tout d'abord, au début, nous avons créé des points d'échantillonnage pour évaluer le modèle d'approximation de Kriging. Ceci est différent du point de LHS (échantillonnage super carré latin). La plage de $ -50 \ leq x, y \ leq 50 $ est évaluée par 25 x 25 points d'échantillonnage divisés en 25.
sg = prob.root.parabo_mm._init_unknowns_dict["f_xy"]["surrogate"]Avec des variables de classe privées(_init_unknowns_dict)Accéder,Chargement du modèle de substitution installé dans Meata Model.
Ce n'est pas un compliment, mais il y a deux raisons à cela.
* L'enregistrement d'un modèle d'approximation entraîné n'est pas implémenté. Cette fois, il a été sérialisé avec pickele.
* Lorsque vous essayez d'évaluer la valeur d'un modèle approximatif avec MetaModel, cela devient un peu compliqué (`` `` # xyzkrig = ・ ・ ・ `` sous la ligne de commentaire).
Le reste est en train de comploter.
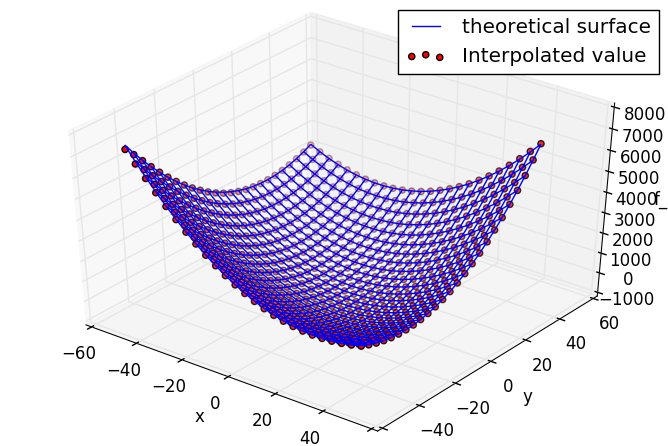
La solution théorique est tracée sur un fil de fer avec des points des valeurs d'évaluation du modèle d'approximation de Kriging.
# Interpolation des valeurs par modèle d'approximation de krigeage
La précision semble assez bonne car le nombre d'échantillons LHS était trop important.
---