Collection d'exemples NumPy pour ceux qui ne sont pas bons en mathématiques
NumPy est un module d'extension pour Python qui est utile pour effectuer des calculs scientifiques et technologiques, en particulier pour les calculs matriciels et multidimensionnels.
Mais même si vous n'utilisez pas les mathématiques, NumPy est utile. En particulier, il peut être plus pratique d'utiliser un tableau de NumPy au lieu d'utiliser plusieurs listes comme «[[1,2], [3,4], [5,6]]».
Cette fois, je voudrais présenter l'utilisation des tableaux principalement dans NumPy avec des exemples.
introduction
NumPy est une bibliothèque pour les mathématiques, mais certaines parties des tableaux NumPy peuvent être utilisées facilement indépendamment des mathématiques. Cependant, de nombreux exemples sur le Web sont destinés à des personnes qui les utilisent en mathématiques, et j'ai pensé qu'il serait difficile de comprendre comment les utiliser dans d'autres domaines que les mathématiques.
Par conséquent, le but de cet article est de présenter la commodité (principalement des tableaux) de NumPy en illustrant certains usages qui ont peu à voir avec les mathématiques.
Je ne suis pas bon en mathématiques et je ne les utilise pas, donc je peux à peine le comprendre.
Bien sûr, la programmation n'est pas un peu liée aux mathématiques, cela ne signifie donc pas que vous ne l'utilisez pas du tout. Les mathématiques mentionnées ici se réfèrent à l'utilisation d'exprimer des formules mathématiques utilisées dans les matrices et l'intégration différentielle par programmation.
Un petit truc mathématique est inclus dans une partie du contenu, mais même si vous ne le comprenez pas, il n'est pas lié au sujet principal, alors veuillez le lire sans vous en soucier.
Précautions d'emploi
Les exemples fournis ici fournissent des conseils pour apprendre à manipuler les données, et le code fourni n'est pas toujours efficace.
Lorsque vous l'utilisez en cours, assurez-vous de le vérifier vous-même.
Lecteurs cibles
Utilisateurs Python qui n'ont jamais utilisé NumPy. Surtout pour ceux qui ne sont pas bons en mathématiques et qui évitent NumPy, et ceux qui n'ont aucun lien avec les mathématiques et n'utilisent pas NumPy.
Environnement d'exécution
OS, système de traitement, etc.
L'environnement dans lequel l'opération a été confirmée est principalement ce ↓.
- Python 3.5.2 | Anaconda 4.1.1 (64-bit)
- Windows 7 64bit
Je ne les ai pas tous vérifiés, mais je n'ai pas traité de ceux qui dépendent du système d'exploitation en particulier. Les résultats concernent principalement les environnements interactifs, mais il existe également des endroits où Jupyter Notebook est utilisé.
Outil de module que vous utilisez
Parmi les éléments suivants, le seul module standard est «calendrier».
| Nom du module | version | La description |
|---|---|---|
| NumPy | 1.11.1 | Module de bibliothèque de calcul numérique qui sera cette fois le rôle principal |
| calendar | (3.5.2) | Module standard pour travailler avec des calendriers texte |
| PIL | 1.1.7 | Module de traitement d'image |
| Matplotlib | 1.5.1 | Module pour tracer des graphiques Cette fois utilisée pour l'affichage de l'image |
| Jupyter Notebook | 4.2.1 | REPL qui peut être utilisé sur un navigateur Web |
- La version de Jupyter Notebook est celle de Notebook Server.
Notions de base
Pour utiliser le module NumPy numpy, il est courant d'utiliser l'alias np.
C'est également le cas de la référence officielle.
import numpy as np
Cet article fait de même. Dans le texte, toujours lu comme importé, même si cet import n'est pas présent.
Le tableau NumPy a le type «numpy.ndarray» (ci-après dénommé «tableau NumPy» dans le texte).
>>> np.array([1, 2])
array([1, 2])
>>> type(np.array([1, 2]))
<class 'numpy.ndarray'>
Cela ressemble à une liste standard, mais le tableau NumPy est beaucoup plus riche que cela. Voir l'article lié ci-dessous pour les différences de nature par rapport à la liste standard.
Bases de NumPy Array - Rencontre avec Python pour l'apprentissage automatique http://www.kamishima.net/mlmpyja/nbayes1/ndarray.html
Conversion de calendrier texte du tableau 1D en 2D
Un calendrier texte est un calendrier qui affiche un calendrier texte sur la console.
Le calendrier texte est également généré par la commande cal dans l'environnement de type Unix.
En fait, le module Python standard a un module «calendrier» qui gère le «calendrier texte» lui-même.
calendrier - Gestion des dates - Module Python de la semaine http://ja.pymotw.com/2/calendar/
Donc, vous n'avez pas à vous soucier de le faire à partir de zéro, mais c'était un sujet facile à comprendre comme exemple d'utilisation de NumPy, alors je l'ai repris.
Dans cette section, nous verrons comment le gérer avec presque aucun module calendrier.
J'ai écrit "presque" car pour faire un calendrier texte, il faut calculer le premier jour et le dernier jour du mois, mais ce n'est pas le but de cette fois de penser à ce calcul, donc de le trouver C'est parce qu'il utilise la fonction monthrange () du module `.
Traitement de l'image
Passons maintenant au sujet principal.
Comme vous pouvez le voir en regardant le calendrier réel, le calendrier texte est complet à 90% 9 minutes si vous appliquez les valeurs appropriées à un tableau 2D de taille fixe 7x6. Cependant, je pense que le traitement est gênant s'il est bidimensionnel depuis le début. Il semble préférable de créer les données dans un tableau à une dimension, puis de les convertir en deux dimensions plus tard.
Les tableaux NumPy ont une méthode reshape () qui transforme un tableau à N dimensions en n'importe quelle dimension.
Vous pouvez l'utiliser pour convertir un tableau unidimensionnel en tableau bidimensionnel.
En gros, ce sera OK si vous procédez selon le flux suivant.
・ Premières données vides (1 dimension)
・ 1-31 (1 dimension)
・ Données vides à la fin (1 dimension)
↓ Combiner
・ Premières données vides + 1-31 + Dernières données vides (1 dimension) * La taille est 42
↓ Convertir en 2D(reshape)
・ Premières données vides + 1-31 + dernières données vides (2D)
↓ Convertit chaque élément en chaîne de caractères
・ Données de calendrier (2D)
Générer des données unidimensionnelles
Tout d'abord, utilisez la fonction calendar.monthrange () pour trouver le nombre requis.
>>> import calendar
>>>
>>> w, c = calendar.monthrange(2016, 7)
>>> w #Le premier jour du mois
4
>>> c #Jours du mois
31
Pour le premier jour du mois, le jour qui commence le lundi est renvoyé. Autrement dit, lundi est «0» et dimanche est «6». Cette fois, je veux faire un calendrier qui commence le dimanche, donc je vais le corriger.
#(A continué)
>>> w = w + 1 if w < 6 else 0
>>> w
5
Pour créer un tableau avec des zéros définis, utilisez la fonction np.zeros ().
Pour créer un tableau de nombres, utilisez la fonction np.arange (), qui est similaire à la fonction standard range ().
Si vous ne spécifiez pas «dtype», le type de données par défaut est «float64».
#(A continué)
>>> np.zeros(1).dtype
dtype('float64')
>>> np.zeros(1, dtype=int).dtype
dtype('int32')
>>> np.zeros(w, dtype=int)
array([0, 0, 0, 0, 0])
>>> np.arange(start=1, stop=c+1, dtype=int)
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,
18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31])
>>> np.zeros(42 - w - c, dtype=int)
array([0, 0, 0, 0, 0, 0])
Vous pouvez joindre des tableaux avec la fonction np.concatenate ().
Veuillez noter que si vous calculez deux tableaux NumPy avec «+», ce sera un calcul vectoriel / matrice.
#(A continué)
>>> np.array([1, 2]) + np.array([3, 4])
array([4, 6]) #Somme en tant que vecteur
>>> headfiller = np.zeros(w, dtype=int)
>>> days = np.arange(start=1, stop=c+1, dtype=int)
>>> tailfiller = np.zeros(42 - w - c, dtype=int)
>>> np.concatenate((headfiller, days, tailfiller))
array([ 0, 0, 0, 0, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,
13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29,
30, 31, 0, 0, 0, 0, 0, 0])
Vous pouvez également préparer 42 zéros en premier et les écraser avec la séquence de jours. Dans ce cas, veuillez noter qu'une erreur se produira si la taille du tableau à écraser et la taille de la plage ne correspondent pas.
#(A continué)
>>> days = np.zeros(42, dtype=int)
>>> days[w:w+c] = np.arange(start=1, stop=c+1, dtype=int)
>>> days
array([ 0, 0, 0, 0, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,
13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29,
30, 31, 0, 0, 0, 0, 0, 0])
S'il est plus facile de générer à partir d'une liste standard, convertissez-la ultérieurement en tableau NumPy avec la fonction np.array ().
dtype conserve le type de la liste d'origine.
#(A continué)
>>> days = np.array([0] * w + list(range(1, c+1)) + [0] * (42 - w - c))
>>> days.dtype
dtype('int32')
>>> days
array([ 0, 0, 0, 0, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,
13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29,
30, 31, 0, 0, 0, 0, 0, 0])
Vous disposez maintenant d'un calendrier matriciel unidimensionnel.
Convertir un tableau à une dimension en un tableau à deux dimensions
Ensuite, convertissez-le en un tableau à deux dimensions. Puisque la dimension est spécifiée dans l'ordre des lignes et des colonnes, elle sera «(6, 7)».
#(A continué)
>>> days.reshape((6, 7))
array([[ 0, 0, 0, 0, 0, 1, 2],
[ 3, 4, 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14, 15, 16],
[17, 18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29, 30],
[31, 0, 0, 0, 0, 0, 0]])
Après cela, convertissez la valeur numérique en représentation sous forme de chaîne de caractères et les données sont terminées.
Convertir chaque élément en une représentation sous forme de chaîne
Pour créer une nouvelle liste en transformant chaque élément de la liste, les fonctions standard utilisent la fonction map () et la notation d'inclusion de liste.
Pour faire de même avec un tableau de NumPy, utilisez la fonction np.vectorize ().
#(A continué)
>>> mapper = np.vectorize(lambda x: " " if x == 0 else "%2d" % x)
>>> mapper
<numpy.lib.function_base.vectorize object at 0x0000000002D3C668>
>>> mapper(days.reshape((6, 7)))
array([[' ', ' ', ' ', ' ', ' ', ' 1', ' 2'],
[' 3', ' 4', ' 5', ' 6', ' 7', ' 8', ' 9'],
['10', '11', '12', '13', '14', '15', '16'],
['17', '18', '19', '20', '21', '22', '23'],
['24', '25', '26', '27', '28', '29', '30'],
['31', ' ', ' ', ' ', ' ', ' ', ' ']],
dtype='<U2')
L'objet fonction créé par vectorize est comme une application partielle de la fonction de conversion à la fonction map ().
L'application d'un tableau à cet objet fonction renverra un tableau mappé.
L'ordre de traitement de ce mappage et de "remodeler" peut être inversé.
Tout ce que vous avez à faire est de combiner et de sortir. Décorez comme vous le souhaitez.
#(A continué)
>>> strdays2d = mapper(days.reshape((6, 7)))
>>> print("\n".join([" ".join(x) for x in strdays2d]))
1 2
3 4 5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23
24 25 26 27 28 29 30
31
Version terminée
Enfin, je posterai un résumé des fonctions.
--Code Python pour calendrier texte
import numpy as np
import calendar
def print_calendar(y, m):
w, c = calendar.monthrange(y, m)
w = w + 1 if w < 6 else 0
#Version prise en sandwich entre des tableaux zéro
headfiller = np.zeros(w, dtype=int)
tailfiller = np.zeros(42 - w - c, dtype=int)
days = np.concatenate((headfiller, np.arange(start=1, stop=c+1, dtype=int), tailfiller))
#La version qui fait zéro en premier
# days = np.zeros(42, dtype=int)
# days[w:w+c] = np.arange(start=1, stop=c+1, dtype=int)
#Version réalisée à partir de la liste standard
# days = np.array([0] * w + list(range(1, c+1)) + [0] * (42 - w - c))
mapper = np.vectorize(lambda x: " " if x == 0 else "%2d" % x)
strdays2d = mapper(days).reshape((6, 7))
print("%d %d" % (y, m))
print()
print("\n".join([" ".join(x) for x in strdays2d]))
if __name__ == "__main__":
print_calendar(2016, 8)
- Résultat d'exécution
2016 8
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
Bitmap - Génère une image à partir d'un tableau 2D + 1D
Le bitmap qui représente l'image se compose d'un tableau bidimensionnel de coordonnées XY et d'informations qui représentent la couleur de chaque pixel. Exprimons cela avec un tableau bidimensionnel de NumPy.
Le module utilisé cette fois exprime les couleurs dans un tableau de taille 3 ([R, V, B]), nous allons donc les combiner et les exprimer en 3 dimensions.
En fonction de la bibliothèque, il peut être spécifié dans le nom de la couleur ou au format # rrggbb, donc dans ce cas, il sera exprimé comme un tableau bidimensionnel de ʻint ou str`.
Le module PIL a de nombreuses fonctions pour le traitement d'images, donc si vous voulez traiter les images sérieusement, veuillez utiliser pleinement ces fonctions.
Générer une image avec PIL
Pour générer une image à partir d'un tableau de NumPy dans PIL:
import numpy as np
from PIL import Image
imgdata = np.zeros((16, 16, 3), dtype=np.uint8)
imgdata[:] = [255, 0, 0]
im = Image.fromarray(imgdata)
im.show() #S'affiche sous forme de fichier BMP dans la visionneuse d'images sous Windows
im.save("/path/to/image.png ", "PNG")
Vous pouvez attribuer la même valeur à tous les éléments en deux dimensions en définissant ʻimgdata [:] = ... `. (Le fait est qu'il n'est pas tridimensionnel.)
ʻCréez un objet image avec la fonction Image.fromarray () . Lorsque la méthode show ()est exécutée, elle sera affichée dans la visionneuse d'images du système d'exploitation. Vous pouvez enregistrer l'image dans un fichier en exécutant la méthodesave ()`.
L'exécution de ce code générera un fichier image PNG rempli de rouge 16x16.
Dessiner avec Matplotlib sur Jupyter Notebook
Un moyen plus simple consiste à utiliser Matplotlib. Pour afficher l'image directement générée sur le bloc-notes Jupyter, exécutez le code suivant. Les données sont les mêmes que pour PIL.
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
imgdata = np.zeros((16, 16, 3), dtype=np.uint8)
imgdata[:] = [255, 0, 0]
# plt.figure(figsize = (1.75, 1.75)) #Environ la taille réelle lorsque la taille est de 100x100
# plt.axis("off") #Ne pas montrer l'échelle
plt.imshow(imgdata)
# plt.show() #Effacer la représentation sous forme de chaîne de l'objet
Cette méthode met automatiquement à l'échelle la taille de l'image par défaut. De plus, comme il est affiché sous forme de graphique, la mémoire est affichée. Vous pouvez utiliser le code commenté dans l'exemple de code pour redimensionner ou afficher uniquement l'image.
Dans les exemples qui suivent, ce paramètre est redondant, nous n'utilisons donc que la fonction ʻimshow () `.
- Résultat d'exécution

- L'image est réduite. (La même chose s'applique ci-dessous.)
À partir de ce moment, celui exécuté par Jupyter Notebook est publié, donc si vous n'utilisez pas Jupyter Notebook, veuillez le lire comme le code qui génère le fichier avec PIL.
Processus en boucle
Ici, nous allons voir comment manipuler le tableau multidimensionnel de NumPy via la manipulation de bitmap.
Faisons une image 100x100. Ensuite, laissez le vert correspondre aux valeurs numériques de «x» et «y» et changez la valeur.
Les tableaux NumPy sont conçus pour gérer naturellement les tableaux multidimensionnels, tels que ʻimgdata [y, x] `. Il convient de noter que l'accès à un tableau à deux dimensions est «[y, x]» car la première dimension signifie la direction verticale et la deuxième dimension signifie la direction horizontale.
L'exemple suivant est le processus de définition des informations de couleur pour chaque élément d'une boucle. Seule la valeur verte est modifiée à l'aide des valeurs «x» et «y».
%matplotlib inline
from matplotlib.pyplot import imshow
import numpy as np
w, h = 100, 100 #largeur et hauteur
imgdata = np.zeros((w, h, 3), dtype=np.uint8)
for x, y in [(x, y) for x in range(w) for y in range(h)]:
imgdata[y, x] = [0, x + y, 0]
imshow(imgdata)
- Résultat d'exécution
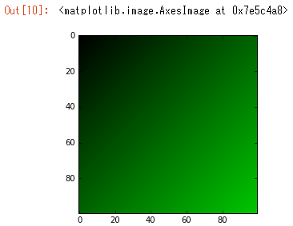
J'ai pu dessiner une gradation verte.
Processus dans la plage
Vous pouvez également spécifier une plage et y définir la même valeur.
En définissant [10:30, 50:80], tous les éléments de la plage rectangulaire dont les sommets sont (50, 10), (50, 30), (80, 30), (80, 10) Peut être spécifié.
%matplotlib inline
from matplotlib.pyplot import imshow
import numpy as np
w, h = 100, 100
imgdata = np.zeros((w, h, 3), dtype=np.uint8)
imgdata[10:30, 50:80] = [0, 0, 255]
imshow(imgdata)
- Résultat d'exécution

variation
Vous pouvez les combiner pour dessiner des motifs et des figures.
Le code suivant est un exemple de dessin d'une image en combinant le traitement en boucle et le traitement par plage.
- La fonction sin et la fonction cos servent à obtenir des valeurs périodiques, et la connaissance des mathématiques n'est pas pertinente ici, vous n'avez donc pas à réfléchir sérieusement.
- Exemple de code Python pour dessiner un motif et plusieurs rectangles
%matplotlib inline
from matplotlib.pyplot import imshow
import numpy as np
from math import sin, cos
w, h = 100, 100
a = np.zeros((w, h, 3), dtype=np.uint8)
for x, y in [(x, y) for x in range(w) for y in range(h)]:
v = int(127 + sin(x * 0.6) * cos(y * 0.6) * 128)
a[y, x] = [v, v, 0]
a[10:30, 10:70] = [int("ff", 16), int("66", 16), 0]
a[20:50, 20:80] = [int("ff", 16), int("cc", 16), 0]
a[30:70, 30:90] = [int("66", 16), int("ff", 16), 0]
imshow(a)
- Résultat d'exécution

Tranches de récupération numérique (tableaux partiels) telles que des lignes et des colonnes
Une place numérique ou une place numérique est un type de puzzle numérique. C'est un puzzle qui remplit les nombres 1 à 9 dans le tableau 9x9 afin que les mêmes nombres n'entrent pas verticalement, horizontalement et 3x3.
Sugoku-Wikipédia https://ja.wikipedia.org/wiki/%E6%95%B0%E7%8B%AC
Faisons un programme pour résoudre les mathématiques en utilisant le tableau bidimensionnel de NumPy. Vous n'avez pas besoin d'en connaître quelques-uns car nous n'avons affaire qu'à une logique très simple ici.
La logique la plus simple pour remplir un nombre est de rechercher un nombre qui n'est pas utilisé verticalement, horizontalement ou 3x3 dans un carré. Le tableau NumPy est utile pour récupérer des listes de nombres verticales, horizontales et 3x3. Cependant, le tableau NumPy seul peut être un peu encombrant, utilisez-le donc en combinaison avec le type de collection standard.
Utilisez le tableau bidimensionnel suivant comme exemple de données en question. Zéro indique une cellule vide.
grid = np.array([
[3, 0, 0, 0, 0, 9, 0, 0, 8],
[0, 0, 0, 0, 0, 6, 7, 0, 0],
[9, 8, 2, 0, 0, 0, 6, 0, 0],
[0, 9, 0, 0, 3, 0, 4, 0, 0],
[0, 3, 5, 0, 0, 0, 2, 1, 0],
[0, 0, 7, 0, 2, 0, 0, 9, 0],
[0, 0, 4, 0, 0, 0, 9, 7, 5],
[0, 0, 9, 6, 0, 0, 0, 0, 0],
[8, 0, 0, 4, 0, 0, 0, 0, 2],
])
Sortez une tranche (tableau partiel)
Lorsque 9x9 est représenté par une liste multiple standard, il est difficile de récupérer une liste de colonnes ou une liste de 3x3, en dehors de la liste des lignes.
NumPy facilite le fonctionnement en tant que table bidimensionnelle.
Par souci de clarté, nous avons fourni des images numérotées et colorées des problèmes en Allemagne.

Découvrons la masse «f4» en nous référant à cette image.
Extrayez la colonne de «f» (vert), la ligne de «4» (beige) et le 3x3 (jaune) de «d4-f6».
Puisque 3x3 est pris comme un tableau bidimensionnel, il est converti en unidimensionnel en utilisant la méthode reshape ().
Le tableau extrait est converti en «liste» pour une facilité d'utilisation.
Comme mentionné dans la section sur les bitmaps, l'accès à un tableau bidimensionnel signifie que la première dimension est verticale et la deuxième dimension est horizontale. Veuillez noter que c'est «[y, x]», pas «[x, y]».
Vous pouvez obtenir des tranches (tableaux partiels) en faisant quelque chose comme grid [:, 5], grid [3,:], grid [3: 6, 3: 6].
Si vous utilisez la même spécification de plage dans une expression d'affectation, vous pouvez affecter à la plage entière, comme indiqué dans la section Bitmap.
#(A continué)
>>> list(grid[:, 5]) #Colonne f: x=5 colonnes
[9, 6, 0, 0, 0, 0, 0, 0, 0]
>>> list(grid[3, :]) #Ligne 4: y=3 rangées
[0, 9, 0, 0, 3, 0, 4, 0, 0]
>>> list(grid[3:6, 3:6].reshape(9)) # d4-f6
[0, 3, 0, 0, 0, 0, 0, 2, 0]
Agréger la liste des numéros
À partir de là, nous traiterons sans utiliser le tableau NumPy.
Une fois que vous avez une liste de colonnes, une liste de lignes et une liste 3x3, vous pouvez les combiner et les convertir en type set pour obtenir une liste unique de nombres déjà utilisés.
#(A continué)
>>> used_nums = set(list(grid[:, 5]) + list(grid[3, :]) + list(grid[3:6, 3:6].reshape(9)))
>>> used_nums
{0, 2, 3, 4, 6, 9}
Vous n'avez pas besoin d'un zéro, mais c'est normal d'en avoir un, alors laissez-le tel quel. ʻUsed_nums- {0} `peut être utilisé pour supprimer les zéros.
Si vous supprimez les numéros déjà utilisés de la séquence de numéros de 1 à 9, vous aurez des numéros candidats.
Utilisez l'opération - de type set pour supprimer les nombres utilisés.
#(A continué)
# range(1, 10)Est un nombre de 1 à 9
>>> unused_nums = set(range(1, 10)) - used_nums
>>> unused_nums
{8, 1, 5, 7}
S'il n'y a qu'un seul nombre inutilisé, il déterminera le nombre dans ce carré. «f4» n'a pas pu être réduit à un dans l'état actuel.
Regardons aussi c2.
#(A continué)
>>> col = list(grid[:, 2]) #Colonne c: x=2 colonnes
>>> row = list(grid[1, :]) #Ligne 2: y=1 ligne
>>> sq = list(grid[0:3, 0:3].reshape(9)) # a1-c3
>>> col, row, sq
([0, 0, 2, 0, 5, 7, 4, 9, 0], [0, 0, 0, 0, 0, 6, 7, 0, 0], [3, 0, 0, 0, 0, 0, 9, 8, 2])
>>> used_nums = set(col + row + sq)
>>> used_nums
{0, 2, 3, 4, 5, 6, 7, 8, 9}
>>> unused_nums = set(range(1, 10)) - used_nums
>>> unused_nums
{1}
Cette fois, le nombre a été réduit à seulement «1». Ainsi, il a été confirmé que «1» sera inclus dans «c2».
Version terminée (en développement)
En appliquant à plusieurs reprises la logique jusqu'à ce point aux cellules non remplies, le programme de résolution du nombre d'Allemands est terminé pour le moment.
Cependant, si vous ne pouvez pas remplir ne serait-ce qu'une case en un tour, vous abandonnerez. En l'état, il implémente uniquement la logique de base dans les bases, donc il ne sera résolu que s'il s'agit d'un problème très simple.
Je posterai le code de l'exemple complété.
--Exemple de code Python pour résoudre les mathématiques (version qui ne peut résoudre que des problèmes simples)
import numpy as np
grid = np.array([
[3, 0, 0, 0, 0, 9, 0, 0, 8],
[0, 0, 0, 0, 0, 6, 7, 0, 0],
[9, 8, 2, 0, 0, 0, 6, 0, 0],
[0, 9, 0, 0, 3, 0, 4, 0, 0],
[0, 3, 5, 0, 0, 0, 2, 1, 0],
[0, 0, 7, 0, 2, 0, 0, 9, 0],
[0, 0, 4, 0, 0, 0, 9, 7, 5],
[0, 0, 9, 6, 0, 0, 0, 0, 0],
[8, 0, 0, 4, 0, 0, 0, 0, 2]])
nums = set(range(1, 10)) # 1~9
square_table = [0, 0, 0, 3, 3, 3, 6, 6, 6]
def fill(x, y):
if (grid[y, x] != 0):
return 0
list1 = list(grid[:, x]) #Verticale
list2 = list(grid[y, :]) #côté
xx, yy = square_table[x], square_table[y]
list3 = list(grid[yy:yy+3, xx:xx+3].reshape(9)) # 3x3
used_nums = set(list1 + list2 + list3)
unused_nums = nums - used_nums
if len(unused_nums) == 1:
grid[y, x] = list(unused_nums)[0]
return 1
else:
return 0
if __name__ == "__main__":
for i in range(81):
print("loop:", i + 1)
filled = sum([fill(x, y) for x in range(9) for y in range(9)])
if len(grid[grid == 0]) == 0:
print("solved!")
break
if filled == 0:
print("give up...")
break
print(grid)
Un petit supplément à ce code.
Où rempli = somme (...) utilise la notation d'inclusion de liste au lieu de boucles.
En "additionnant le résultat de l'appel de chaque fonction" fill () ", le nombre de cellules remplies dans le tour est calculé.
grid [grid == 0] est l'une des fonctions utiles du tableau NumPy, et vous pouvez récupérer tous les éléments qui correspondent aux conditions.
Ici, grid == 0 est défini, donc tous les éléments nuls sont extraits.
Si vous comptez le nombre de ces éléments, vous pouvez voir le nombre de cellules non remplies.
J'utilise ceci pour vérifier si le problème a été résolu.
Nous utilisons la table de conversion square_table pour calculer la plage 3x3.
Vous pouvez le faire avec quatre règles, mais je pense que c'est plus clair dans ce cas.
- Résultat du traitement
loop: 1
loop: 2
loop: 3
loop: 4
give up...
[[3 0 6 0 0 9 5 0 8]
[0 0 1 0 0 6 7 0 0]
[9 8 2 0 0 0 6 0 0]
[0 9 8 0 3 0 4 5 0]
[0 3 5 0 0 0 2 1 0]
[0 0 7 0 2 0 0 9 0]
[0 0 4 0 0 0 9 7 5]
[0 0 9 6 0 0 0 0 0]
[8 0 3 4 0 0 1 6 2]]
Le premier problème que j'ai mentionné n'a pas pu être résolu par cette seule logique. Si vous êtes intéressé, essayez d'ajouter ou de modifier une logique afin de pouvoir résoudre des problèmes plus avancés.
À propos, le premier exemple publié sur Wikipédia pourrait être résolu avec cette seule logique.
en conclusion
Comme vous pouvez le voir, certains processus sont beaucoup plus flexibles que les listes standard. Il existe de nombreuses autres fonctionnalités dans NumPy, mais celles répertoriées ici devraient être très utiles.
Que vous soyez novice en mathématiques ou que vous n'ayez pas encore utilisé NumPy, veuillez profiter de NumPy.
Matériel de référence
Overview — NumPy v1.11 Manual http://docs.scipy.org/doc/numpy/index.html
100 numpy exercises http://www.labri.fr/perso/nrougier/teaching/numpy.100/
python - How do I convert a numpy array to (and display) an image? - Stack Overflow http://stackoverflow.com/questions/2659312/how-do-i-convert-a-numpy-array-to-and-display-an-image
Recommended Posts