[Apprentissage automatique] Je vais vous expliquer en essayant le cadre d'apprentissage profond Chainer.
Le framework Deep Learning, Chainer, qui est le sujet de discussion, a un exemple de code pour discriminer les caractères manuscrits. Je voudrais écrire un article qui explique un peu le contenu en utilisant cela.
** (Le code complet de cet article a été téléchargé sur GitHub [PC recommandé]) ** **
Quoi qu'il en soit, c'est très facile à installer, et si vous écrivez Python, vous pouvez l'utiliser immédiatement, donc je le recommande! C'est formidable de pouvoir écrire du code en Python.
C'est un article pour essayer un modèle de réseau neuronal comme celui-ci.
Les principales informations peuvent être trouvées ici. Site principal de Chainer Dépôt GitHub de Chainer Tutoriels et références Chainer
1. Numéro d'installation
Tout d'abord, c'est une installation. Après avoir installé les logiciels et les bibliothèques nécessaires, reportez-vous à «Conditions» (https://github.com/pfnet/chainer#requirements) sur GitHub de Chainer.
pip install chainer
Éxécuter. Vous pouvez l'installer avec juste cela. Super facile! J'ai eu beaucoup de mal en essayant d'installer Caffe sur mon Mac, mais cela semble être un mensonge: sourire:
Si vous êtes bloqué dans l'installation, l'article de cvl-robot "Chainer of Deep Learning library semble être étonnant" est détaillé. C'est pratique car il décrit l'installation des bibliothèques nécessaires.
2. Obtenez l'exemple de code
Il existe un exemple dans le répertoire suivant de GitHub qui distingue les caractères manuscrits MNIST familiers, donc j'aimerais l'utiliser comme sujet. Il s'agit d'une tentative de classer cela avec le réseau neuronal à propagation directe de Chainer. https://github.com/pfnet/chainer/tree/master/examples/mnist ┗ train_mnist.py
Je voudrais ajouter un commentaire à ce code et afficher une partie du flux dans un graphique pour ajouter une image.
3. Regardez l'exemple de code
Cette fois, j'écris en vérifiant le fonctionnement de mon Macbook Air (OS X ver 10.10.2), il peut donc y avoir des différences en fonction de l'environnement, mais j'espère que vous pourrez le voir. De plus, en raison de cet environnement, le code lié au GPU est omis car seul le CPU est utilisé sans calcul sur le GPU.
3-1. Préparation
Le premier est l'importation des bibliothèques requises.
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import fetch_mldata
from chainer import cuda, Variable, FunctionSet, optimizers
import chainer.functions as F
import sys
plt.style.use('ggplot')
Ensuite, définissez et définissez divers paramètres.
#Taille de lot pour un lot lors de l'entraînement avec la méthode de descente de gradient probabiliste
batchsize = 100
#Nombre de répétitions d'apprentissage
n_epoch = 20
#Nombre de couches intermédiaires
n_units = 1000
Utilisez Scikit Learn pour télécharger des données numériques manuscrites MNIST.
#Télécharger les données numériques manuscrites du MNIST
# #HOME/scikit_learn_data/mldata/mnist-original.Caché dans le tapis
print 'fetch MNIST dataset'
mnist = fetch_mldata('MNIST original')
# mnist.data : 70,000 données vectorielles 784 dimensions
mnist.data = mnist.data.astype(np.float32)
mnist.data /= 255 # 0-Convertir en 1 données
# mnist.target :Corriger les données de réponse (données de l'enseignant)
mnist.target = mnist.target.astype(np.int32)
Je vais en retirer environ 3 et dessiner.
#Fonction pour dessiner des données numériques manuscrites
def draw_digit(data):
size = 28
plt.figure(figsize=(2.5, 3))
X, Y = np.meshgrid(range(size),range(size))
Z = data.reshape(size,size) # convert from vector to 28x28 matrix
Z = Z[::-1,:] # flip vertical
plt.xlim(0,27)
plt.ylim(0,27)
plt.pcolor(X, Y, Z)
plt.gray()
plt.tick_params(labelbottom="off")
plt.tick_params(labelleft="off")
plt.show()
draw_digit(mnist.data[5])
draw_digit(mnist.data[12345])
draw_digit(mnist.data[33456])
Ce sont les données du vecteur dimensionnel 28x28,784.

Divisez l'ensemble de données en données de validation des données d'entraînement.
#Définir N données d'entraînement et les données de vérification restantes
N = 60000
x_train, x_test = np.split(mnist.data, [N])
y_train, y_test = np.split(mnist.target, [N])
N_test = y_test.size
3.2 Définition du modèle
C'est finalement la définition du modèle. C'est la production d'ici. Utilisez les classes et fonctions Chainer.
# Prepare multi-layer perceptron model
#Paramètres du modèle Perceptron multicouche
#Dimensions d'entrée 784, dimensions de sortie 10
model = FunctionSet(l1=F.Linear(784, n_units),
l2=F.Linear(n_units, n_units),
l3=F.Linear(n_units, 10))
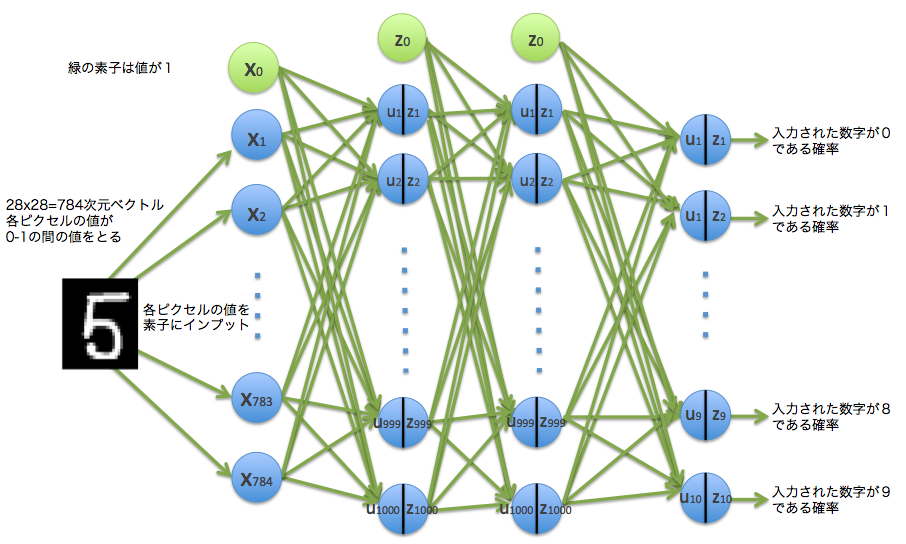
Puisque les données numériques manuscrites d'entrée sont un vecteur de 784 dimensions, il y a 784 éléments d'entrée. Cette fois, la couche intermédiaire est spécifiée comme 1000 en n_units. La sortie est 10 car elle identifie le nombre. Ci-dessous, une image de ce modèle.

La structure de propagation directe est définie par la fonction forward () ci-dessous.
# Neural net architecture
#Structure du réseau neuronal
def forward(x_data, y_data, train=True):
x, t = Variable(x_data), Variable(y_data)
h1 = F.dropout(F.relu(model.l1(x)), train=train)
h2 = F.dropout(F.relu(model.l2(h1)), train=train)
y = model.l3(h2)
#Puisqu'il s'agit d'une classification multi-classes, la fonction softmax en tant que fonction d'erreur
#Dérivation de l'erreur à l'aide de la fonction d'entropie croisée
return F.softmax_cross_entropy(y, t), F.accuracy(y, t)
Je voudrais expliquer chaque fonction ici. Dans la méthode de Chainer, les données sont converties d'un tableau en un objet de type (classe) appelé Variable of Chainer et utilisées.
x, t = Variable(x_data), Variable(y_data)
La fonction d'activation n'est pas la fonction sigmoïde, mais la fonction F.relu ().
F.relu(model.l1(x))
Ce F.relu () est une fonction d'unité linéaire rectifiée
f(x) = \max(0, x)
En d'autres termes

C'est comme ça. Cliquez ici pour le code de dessin.
# F.test relu
x_data = np.linspace(-10, 10, 100, dtype=np.float32)
x = Variable(x_data)
y = F.relu(x)
plt.figure(figsize=(7,5))
plt.ylim(-2,10)
plt.plot(x.data, y.data)
plt.show()
C'est une fonction simple. Pour cette raison, il semble que l'avantage est que la quantité de calcul est faible et que la vitesse d'apprentissage est rapide.
Ensuite, la fonction F.dropout () est utilisée avec la sortie de cette fonction relu () comme entrée.
F.dropout(F.relu(model.l1(x)), train=train)
Cette fonction d'abandon F.dropout () a été proposée dans l'article Dropout: A Simple Way to Prevent Neural Networks from Overfitting. Il semble qu'il soit possible d'éviter le surapprentissage en abandonnant aléatoirement la couche intermédiaire (en supposant qu'elle n'existe pas) par la méthode.
Bougeons un peu.
# dropout(x, ratio=0.5, train=True)tester
# x:Valeur d'entrée
# ratio:Probabilité de sortie 0
# train:Si False, renvoie x tel quel
# return:0 avec une probabilité de rapport, probabilité de rapport 1,x*(1/(1-ratio))Renvoie la valeur de
n = 50
v_sum = 0
for i in range(n):
x_data = np.array([1,2,3,4,5,6], dtype=np.float32)
x = Variable(x_data)
dr = F.dropout(x, ratio=0.6,train=True)
for j in range(6):
sys.stdout.write( str(dr.data[j]) + ', ' )
print("")
v_sum += dr.data
#La moyenne de sortie est x_Correspond approximativement aux données
sys.stdout.write( str((v_sum/float(n))) )
output
2.5, 5.0, 7.5, 0.0, 0.0, 0.0,
2.5, 5.0, 7.5, 10.0, 0.0, 15.0,
0.0, 5.0, 7.5, 10.0, 12.5, 15.0,
・ ・ ・
0.0, 0.0, 7.5, 10.0, 0.0, 0.0,
2.5, 0.0, 7.5, 10.0, 0.0, 15.0,
[ 0.94999999 2.29999995 3. 3.5999999 7.25 5.69999981]
Passez le tableau [1,2,3,4,5,6] à la fonction F.dropout (). Maintenant, le ratio est le taux d'abandon, et puisque ratio = 0,6 est fixé, il y a 60% de chances qu'il soit abandonné et que 0 soit produit. La valeur est renvoyée avec une probabilité de 40%, mais à ce moment-là, la probabilité de renvoyer la valeur a été réduite à 40%, donc pour compenser, $ {1 \ sur 0,4} $ fois = 2,5 fois La valeur est sortie. En d'autres termes
(0 \times 0.6 + 2.5 \times 0.4) = 1
Donc, en moyenne, c'est le numéro d'origine. Dans l'exemple ci-dessus, la dernière ligne est la moyenne de la sortie, mais elle est répétée 50 fois et la valeur est proche de l'original [1,2,3,4,5,6].
Il existe une autre couche de la même structure et la valeur de sortie est $ y $.
h2 = F.dropout(F.relu(model.l2(h1)), train=train)
y = model.l3(h2)
La sortie finale est la sortie d'erreur utilisant la fonction softmax et la fonction d'entropie croisée. Et la fonction F.accuracy () renvoie la précision.
#Puisqu'il s'agit d'une classification multi-classes, la fonction softmax en tant que fonction d'erreur
#Dérivation de l'erreur à l'aide de la fonction d'entropie croisée
return F.softmax_cross_entropy(y, t), F.accuracy(y, t)
Bien qu'il s'agisse d'une fonction softmax,
y_k = z_k = f_{k}({\bf u})={\exp(u_{k}) \over \sum_j^K \exp(u_{j})}
En intercalant cette fonction avec une fonction définie comme, la somme des 10 sorties de $ y_1, \ cdots, y_ {10} $ devient 1, et les sorties peuvent être interprétées comme des probabilités. Je comprends que la raison pour laquelle la fonction $ \ exp () $ est utilisée est que la valeur ne doit pas être négative.
La fonction familière $ \ exp () $ est
 Puisqu'il a une forme comme, il ne prend pas de valeur négative. En conséquence, la valeur ne devient pas négative et le total est 1, ce qui peut être interprété comme une probabilité.
En utilisant la valeur de sortie $ y_k $ de la fonction Softmax, la fonction d'entropie croisée
Puisqu'il a une forme comme, il ne prend pas de valeur négative. En conséquence, la valeur ne devient pas négative et le total est 1, ce qui peut être interprété comme une probabilité.
En utilisant la valeur de sortie $ y_k $ de la fonction Softmax, la fonction d'entropie croisée
E({\bf w}) = -\sum_{n=1}^{N} \sum_{k=1}^{K} t_{nk} \log y_k ({\bf x}_n, {\bf w})
Il est exprimé comme.
Dans le code Chainer, https://github.com/pfnet/chainer/blob/master/chainer/functions/softmax_cross_entropy.py C'est dedans,
def forward_cpu(self, inputs):
x, t = inputs
self.y, = Softmax().forward_cpu((x,))
return -numpy.log(self.y[xrange(len(t)), t]).sum(keepdims=True) / t.size,
Correspond à.
De plus, F.accuracy (y, t) correspond à la sortie avec les données de l'enseignant et renvoie le taux de réponse correct.
3.3 Paramètres de l'optimiseur
Maintenant que le modèle a été décidé, passons à la formation. Adam est utilisé ici comme méthode d'optimisation.
# Setup optimizer
optimizer = optimizers.Adam()
optimizer.setup(model.collect_parameters())
Echizen_tm explique Adam dans Adam en 30 minutes. Je suis.
4. Mise en œuvre et résultats de la formation
À partir des préparations ci-dessus, nous discriminerons les nombres manuscrits par apprentissage par mini-lots et vérifierons l'exactitude.
train_loss = []
train_acc = []
test_loss = []
test_acc = []
l1_W = []
l2_W = []
l3_W = []
# Learning loop
for epoch in xrange(1, n_epoch+1):
print 'epoch', epoch
# training
#Trier aléatoirement l'ordre de N pièces
perm = np.random.permutation(N)
sum_accuracy = 0
sum_loss = 0
#Apprentissage à l'aide de données de 0 à N pour chaque taille de lot
for i in xrange(0, N, batchsize):
x_batch = x_train[perm[i:i+batchsize]]
y_batch = y_train[perm[i:i+batchsize]]
#Initialiser le dégradé
optimizer.zero_grads()
#Calculer l'erreur et la précision par propagation directe
loss, acc = forward(x_batch, y_batch)
#Calculer le gradient par propagation de retour d'erreur
loss.backward()
optimizer.update()
train_loss.append(loss.data)
train_acc.append(acc.data)
sum_loss += float(cuda.to_cpu(loss.data)) * batchsize
sum_accuracy += float(cuda.to_cpu(acc.data)) * batchsize
#Afficher l'erreur des données d'entraînement et la précision des réponses correctes
print 'train mean loss={}, accuracy={}'.format(sum_loss / N, sum_accuracy / N)
# evaluation
#Calculer l'erreur et corriger la précision des réponses à partir des données de test et vérifier les performances de généralisation
sum_accuracy = 0
sum_loss = 0
for i in xrange(0, N_test, batchsize):
x_batch = x_test[i:i+batchsize]
y_batch = y_test[i:i+batchsize]
#Calculer l'erreur et la précision par propagation directe
loss, acc = forward(x_batch, y_batch, train=False)
test_loss.append(loss.data)
test_acc.append(acc.data)
sum_loss += float(cuda.to_cpu(loss.data)) * batchsize
sum_accuracy += float(cuda.to_cpu(acc.data)) * batchsize
#Afficher l'erreur dans les données de test et la précision de la réponse
print 'test mean loss={}, accuracy={}'.format(sum_loss / N_test, sum_accuracy / N_test)
#Enregistrer les paramètres appris
l1_W.append(model.l1.W)
l2_W.append(model.l2.W)
l3_W.append(model.l3.W)
#Précision et erreur du dessin graphique
plt.figure(figsize=(8,6))
plt.plot(range(len(train_acc)), train_acc)
plt.plot(range(len(test_acc)), test_acc)
plt.legend(["train_acc","test_acc"],loc=4)
plt.title("Accuracy of digit recognition.")
plt.plot()
Voici le résumé du résultat pour chaque époque. Il peut être distingué avec une précision élevée d'environ 98,5% en tournant 20 fois.
output
epoch 1
train mean loss=0.278375425202, accuracy=0.914966667456
test mean loss=0.11533634907, accuracy=0.964300005436
epoch 2
train mean loss=0.137060894324, accuracy=0.958216670454
test mean loss=0.0765812527167, accuracy=0.976100009084
epoch 3
train mean loss=0.107826075749, accuracy=0.966816672881
test mean loss=0.0749603212342, accuracy=0.97770000577
epoch 4
train mean loss=0.0939164237926, accuracy=0.970616674324
test mean loss=0.0672153823725, accuracy=0.980000005364
epoch 5
train mean loss=0.0831089563683, accuracy=0.973950009048
test mean loss=0.0705943618687, accuracy=0.980100004673
epoch 6
train mean loss=0.0752325405277, accuracy=0.976883343955
test mean loss=0.0732760328815, accuracy=0.977900006771
epoch 7
train mean loss=0.0719517664274, accuracy=0.977383343875
test mean loss=0.063611669606, accuracy=0.981900005937
epoch 8
train mean loss=0.0683009948514, accuracy=0.978566677173
test mean loss=0.0604036964733, accuracy=0.981400005221
epoch 9
train mean loss=0.0621755663728, accuracy=0.980550010701
test mean loss=0.0591542539285, accuracy=0.982400006652
epoch 10
train mean loss=0.0618313539471, accuracy=0.981183344225
test mean loss=0.0693172766063, accuracy=0.982900006175
epoch 11
train mean loss=0.0583098273944, accuracy=0.982000010014
test mean loss=0.0668152360269, accuracy=0.981600006819
epoch 12
train mean loss=0.054178619228, accuracy=0.983533344865
test mean loss=0.0614466062452, accuracy=0.982900005579
epoch 13
train mean loss=0.0532431817259, accuracy=0.98390001148
test mean loss=0.060112986485, accuracy=0.98400000751
epoch 14
train mean loss=0.0538122716064, accuracy=0.983266676267
test mean loss=0.0624165921964, accuracy=0.983300005198
epoch 15
train mean loss=0.0501562882114, accuracy=0.983833344777
test mean loss=0.0688113694015, accuracy=0.98310000658
epoch 16
train mean loss=0.0513108611095, accuracy=0.984533343514
test mean loss=0.0724038232205, accuracy=0.982200007439
epoch 17
train mean loss=0.0471463404785, accuracy=0.985666677058
test mean loss=0.0612579581685, accuracy=0.983600008488
epoch 18
train mean loss=0.0460166006556, accuracy=0.986050010125
test mean loss=0.0654888718335, accuracy=0.984400007725
epoch 19
train mean loss=0.0458772557077, accuracy=0.986433342795
test mean loss=0.0602016936944, accuracy=0.984400007129
epoch 20
train mean loss=0.046333729005, accuracy=0.986433343093
test mean loss=0.0621869922416, accuracy=0.985100006461
Voici un graphique de la précision et de l'erreur de discrimination pour chaque lot. Le rouge correspond aux données d'entraînement et le bleu aux données de test.

Auparavant, un article [Machine learning] méthode k-plus proche voisin (méthode k plus proche voisin) est écrit par soi-même en python et reconnaît les nombres manuscrits Donc, j'essayais aussi de distinguer les chiffres manuscrits, mais la précision à l'époque était d'environ 97%, donc je peux voir qu'elle s'est améliorée un peu plus.
Ce Chiner peut être entièrement utilisé avec du code Python, donc je pense que c'est un très bon framework pour Pythonista. Je n'ai pas encore fait d'apprentissage "profond", c'est juste un réseau de neurones à feedforward, alors j'aimerais écrire un article sur "deep" dans un proche avenir.
5. Réponses correspondantes
Affiche les 100 numéros identifiés. J'en ai extrait 100 au hasard, mais la réponse est presque correcte. Après avoir affiché 100 éléments plusieurs fois, j'ai finalement pu afficher une mauvaise partie, donc un exemple est montré ci-dessous. On a l'impression que les humains sont testés (rires)
 (* 4 sur 2 lignes et 3 colonnes est identifié à tort comme 9)
(* 4 sur 2 lignes et 3 colonnes est identifié à tort comme 9)
plt.style.use('fivethirtyeight')
def draw_digit3(data, n, ans, recog):
size = 28
plt.subplot(10, 10, n)
Z = data.reshape(size,size) # convert from vector to 28x28 matrix
Z = Z[::-1,:] # flip vertical
plt.xlim(0,27)
plt.ylim(0,27)
plt.pcolor(Z)
plt.title("ans=%d, recog=%d"%(ans,recog), size=8)
plt.gray()
plt.tick_params(labelbottom="off")
plt.tick_params(labelleft="off")
plt.figure(figsize=(15,15))
cnt = 0
for idx in np.random.permutation(N)[:100]:
xxx = x_train[idx].astype(np.float32)
h1 = F.dropout(F.relu(model.l1(Variable(xxx.reshape(1,784)))), train=False)
h2 = F.dropout(F.relu(model.l2(h1)), train=False)
y = model.l3(h2)
cnt+=1
draw_digit3(x_train[idx], cnt, y_train[idx], np.argmax(y.data))
plt.show
6. Visualisation du paramètre w de la première couche
Paramètre de couche d'entrée $ w ^ {(1)} $ 784 J'ai mappé un vecteur tridimensionnel en 28x28 pixels et l'ai affiché. 100 sur 1000 sont sélectionnés au hasard. Si vous regardez de plus près, il y en a qui ressemblent à «2», «5» ou «0». Vous pouvez voir l'atmosphère que les entités peuvent être extraites avec les paramètres de la première couche.

def draw_digit2(data, n, i):
size = 28
plt.subplot(10, 10, n)
Z = data.reshape(size,size) # convert from vector to 28x28 matrix
Z = Z[::-1,:] # flip vertical
plt.xlim(0,27)
plt.ylim(0,27)
plt.pcolor(Z)
plt.title("%d"%i, size=9)
plt.gray()
plt.tick_params(labelbottom="off")
plt.tick_params(labelleft="off")
plt.figure(figsize=(10,10))
cnt = 1
for i in np.random.permutation(1000)[:100]:
draw_digit2(l1_W[len(l1_W)-1][i], cnt, i)
cnt += 1
plt.show()
7. Visualisation du paramètre de couche de sortie w
La couche de sortie est une couche qui reçoit 1000 entrées et 10 sorties, mais j'ai aussi essayé de la visualiser. L'endroit où «0» est écrit est le paramètre permettant de distinguer le nombre manuscrit comme «0».
Puisqu'il s'agit d'un vecteur de 1000 dimensions, 24 0 sont ajoutés à la fin pour créer une image 32x32.

#Couche 3
def draw_digit2(data, n, i):
size = 32
plt.subplot(4, 4, n)
data = np.r_[data,np.zeros(24)]
Z = data.reshape(size,size) # convert from vector to 28x28 matrix
Z = Z[::-1,:] # flip vertical
plt.xlim(0,size-1)
plt.ylim(0,size-1)
plt.pcolor(Z)
plt.title("%d"%i, size=9)
plt.gray()
plt.tick_params(labelbottom="off")
plt.tick_params(labelleft="off")
plt.figure(figsize=(10,10))
cnt = 1
for i in range(10):
draw_digit2(l3_W[len(l3_W)-1][i], cnt, i)
cnt += 1
plt.show()
8. Bonus
Le nombre d'éléments dans la couche intermédiaire a été fixé à «[100, 500, 800, 900, 1000, 1100, 1200, 1500, 2000]» et chacun a été distingué. Le graphique résultant est ci-dessous. Avec plus de 500 éléments, nous avons atteint environ 98%, et il semble que le nombre d'éléments au-delà ne change pas beaucoup.

9. Bonus 2: Fonction d'activation
Pour les principales fonctions d'activation préchargées dans Chainer
- ReLu function
- tanh function
- sigmoid function
il y a. Cela ressemble à la figure ci-dessous. C'est une fonction qui se situe entre l'entrée et la sortie de l'élément, et a pour rôle de fixer un seuil d'entrée et de sortie.

#Test de la fonction d'activation
x_data = np.linspace(-10, 10, 100, dtype=np.float32)
x = Variable(x_data)
y = F.relu(x)
plt.figure(figsize=(8,15))
plt.subplot(311)
plt.title("ReLu function.")
plt.ylim(-2,10)
plt.xlim(-6,6)
plt.plot(x.data, y.data)
y = F.tanh(x)
plt.subplot(312)
plt.title("tanh function.")
plt.ylim(-1.5,1.5)
plt.xlim(-6,6)
plt.plot(x.data, y.data)
y = F.sigmoid(x)
plt.subplot(313)
plt.title("sigmoid function.")
plt.ylim(-.2,1.2)
plt.xlim(-6,6)
plt.plot(x.data, y.data)
plt.show()
Article suivant "[Deep Learning] Essayez Autoencoder with Chainer pour visualiser les résultats." Il s'agit d'un article qui implémente Autoencoder, une technologie qui automatise l'extraction de fonctionnalités avec un apprentissage en profondeur.
[Livre de référence] Apprentissage profond (série professionnelle d'apprentissage automatique) Takayuki Okaya
[Site Web de référence] Site principal de Chainer http://chainer.org/ Dépôt GitHub de Chainer https://github.com/pfnet/chainer Tutoriels et références Chainer http://docs.chainer.org/en/latest/ "Dropout: A Simple Way to Prevent Neural Networks from Overfitting" Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, Ruslan Salakhutdinov http://www.cs.toronto.edu/~rsalakhu/papers/srivastava14a.pdf
Recommended Posts