J'ai étudié la méthode X-means qui estime automatiquement le nombre de clusters
Contexte
La dernière fois, Comment trouvez-vous le nombre k optimal pour les k-moyennes? J'ai écrit un article
 ↓
Section des commentaires
↓
Section des commentaires

C'est pourquoi j'ai coché "X-means"
À propos de la méthode X-means qui estime automatiquement le nombre de clusters
- Algorithme d'extension K-means proposé par Pelleg et Moore (2000).
- Déterminez automatiquement le nombre de clusters K
- Concevez k-means dans un algorithme qui se déplace à grande vitesse même avec un grand nombre de données Le point est la différence avec les k-moyennes conventionnelles.
Les deux premiers articles populaires qui apparaissent lorsque vous recherchez sur Google avec "x-means"
- Document de proposition X-means
- Travail japonais
- Un article sur une version améliorée de x-means publié la même année que l'article original ci-dessus
- Ceci est le code d'implémentation de l'auteur dans R publié
Présentation de x-means
--Déterminer le nombre optimal de grappes à l'aide de la répétition séquentielle k-means et des critères d'arrêt de division BIC --Il existe des variations dans la méthode de calcul BIC
- L'idée de base est, en supposant que les données sont gaussiennes distribuées près du centre de gravité.
- Puisque le concept de distribution de probabilité est introduit et que le concept de vraisemblance en est né, --Flow que BIC peut être calculé
--x-means appelle et utilise de manière récursive k-means
-
Les inconvénients des k-means (dépendance de la valeur initiale) sont en cours de dessin.
-
Le cluster change petit à petit à chaque calcul ――Cependant, la taille du cluster est stable, elle peut donc être utilisée comme guide pour le nombre optimal de clusters.
-
Lorsqu'il n'y a pas d'informations de test précédentes, le nombre optimal de grappes peut être obtenu avec une quantité de calcul qui est plus du double de celle des k-moyennes, quelle que soit la méthode de découverte.
Flux de calcul
Le flux brutal est
- K-means avec un petit nombre de clusters
- 2-signifie le cluster résultant, divisez le cluster,
- Si BIC se développe, adoptez
- Revenir à 2
Citation de figue de 1 papier

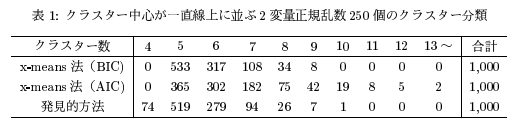
- (Extrait de l'article) Comparaison de la précision lorsque le nombre de clusters corrects est de 5 ――Le nombre de clusters corrects est plus grand lorsqu'il est évalué par BIC que par AIC.
- L'AIC a tendance à produire un nombre relativement important de clusters
- Le résultat de la méthode de découverte (la méthode de spécification manuelle du nombre k avec k-means) est proche du résultat de BIC (si c'est le même que le résultat obtenu manuellement, x-mean qui le fait automatiquement est mieux! )
Différence de logique entre les deux articles
Aperçu du papier original de 1
- Supposons implicitement que tous les clusters ont la même distribution de données
Résumé de 2 papiers logiques améliorés
«Le centre de gravité doit être différent en fonction de la taille de l'amas, nous faisons donc de la logique pour estimer cela également.
Autres articles de blog sur x-means:
- Implémentation de la méthode x-means en Python
- x-means (Dans l'exemple OpenCV, un article qui remplace la réduction de couleur / traitement de division d'image utilisant k-means avec x-means. )
- méthode x-means
- Méthode R de k-means et son extension édition 2 x-means | Journal de sabotage interdit
Script X-means en Python
Implémentation de la méthode x-means en Python [Gist code] Copier / yasaichi / 254a060eff56a3b3b858)
# -*- coding: utf-8 -*-
import numpy as np
from scipy import stats
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from IPython.display import display, HTML #Pour notebook Jupyter
%matplotlib inline
class XMeans:
"""
x-classe qui fait la méthode moyenne
"""
def __init__(self, k_init = 2, **k_means_args):
"""
k_init : The initial number of clusters applied to KMeans()
"""
self.k_init = k_init
self.k_means_args = k_means_args
def fit(self, X):
"""
x-Données de cluster X utilisant la méthode des moyens
X : array-like or sparse matrix, shape=(n_samples, n_features)
"""
self.__clusters = []
clusters = self.Cluster.build(X, KMeans(self.k_init, **self.k_means_args).fit(X))
self.__recursively_split(clusters)
self.labels_ = np.empty(X.shape[0], dtype = np.intp)
for i, c in enumerate(self.__clusters):
self.labels_[c.index] = i
self.cluster_centers_ = np.array([c.center for c in self.__clusters])
self.cluster_log_likelihoods_ = np.array([c.log_likelihood() for c in self.__clusters])
self.cluster_sizes_ = np.array([c.size for c in self.__clusters])
return self
def __recursively_split(self, clusters):
"""
Diviser récursivement les clusters d'arguments
clusters : list-like object, which contains instances of 'XMeans.Cluster'
'XMeans.Cluster'Objet de type liste contenant une instance de
"""
for cluster in clusters:
if cluster.size <= 3:
self.__clusters.append(cluster)
continue
k_means = KMeans(2, **self.k_means_args).fit(cluster.data)
c1, c2 = self.Cluster.build(cluster.data, k_means, cluster.index)
beta = np.linalg.norm(c1.center - c2.center) / np.sqrt(np.linalg.det(c1.cov) + np.linalg.det(c2.cov))
alpha = 0.5 / stats.norm.cdf(beta)
bic = -2 * (cluster.size * np.log(alpha) + c1.log_likelihood() + c2.log_likelihood()) + 2 * cluster.df * np.log(cluster.size)
if bic < cluster.bic():
self.__recursively_split([c1, c2])
else:
self.__clusters.append(cluster)
class Cluster:
"""
k-Une classe qui contient des informations sur le cluster générées par la méthode des moyens et calcule la probabilité et le BIC.
"""
@classmethod
def build(cls, X, k_means, index = None):
if index == None:
index = np.array(range(0, X.shape[0]))
labels = range(0, k_means.get_params()["n_clusters"])
return tuple(cls(X, index, k_means, label) for label in labels)
# index:Un vecteur montrant à quelle ligne des données d'origine appartient l'échantillon de chaque ligne de X
def __init__(self, X, index, k_means, label):
self.data = X[k_means.labels_ == label]
self.index = index[k_means.labels_ == label]
self.size = self.data.shape[0]
self.df = self.data.shape[1] * (self.data.shape[1] + 3) / 2
self.center = k_means.cluster_centers_[label]
self.cov = np.cov(self.data.T)
def log_likelihood(self):
return sum(stats.multivariate_normal.logpdf(x, self.center, self.cov) for x in self.data)
def bic(self):
return -2 * self.log_likelihood() + self.df * np.log(self.size)
if __name__ == "__main__":
import matplotlib.pyplot as plt
#Préparation des données
x = np.array([np.random.normal(loc, 0.1, 20) for loc in np.repeat([1,2], 2)]).flatten() #Générer 80 nombres aléatoires
y = np.array([np.random.normal(loc, 0.1, 20) for loc in np.tile([1,2], 2)]).flatten() #Générer 80 nombres aléatoires
#Exécution du clustering
x_means = XMeans(random_state = 1).fit(np.c_[x,y])
print(x_means.labels_)
print(x_means.cluster_centers_)
print(x_means.cluster_log_likelihoods_)
print(x_means.cluster_sizes_)
#Tracez les résultats
plt.rcParams["font.family"] = "Hiragino Kaku Gothic Pro"
plt.scatter(x, y, c = x_means.labels_, s = 30)
plt.scatter(x_means.cluster_centers_[:,0], x_means.cluster_centers_[:,1], c = "r", marker = "+", s = 100)
plt.xlim(0, 3)
plt.ylim(0, 3)
plt.title("x-means_test1")
plt.legend()
plt.grid()
plt.show()
# plt.savefig("clustering.png ", dpi = 200)
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2]
[[ 1.01854145 2.00982242]
[ 1.00199794 1.02110352]
[ 2.00022392 2.00435037]
[ 2.04408807 1.0518478 ]]
[ 42.91288569 44.48049658 37.32131967 29.6422041 ]
[20 20 20 20]
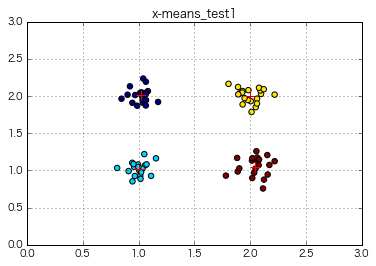
⇒ X-means a été réalisé sur les données de 4 clusters, et il a certainement été divisé en 4 clusters sans spécifier de nombre k explicite!
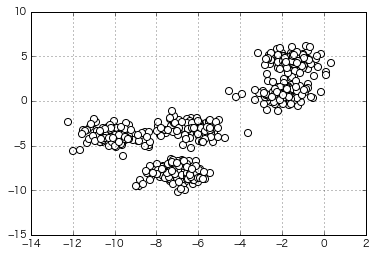
Essayez de regrouper des données qui ressemblent un peu plus à ça
(Le nombre de clusters spécifié au moment de la génération est de 5)
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=500,
n_features=2,
centers=5,
cluster_std=0.8,
center_box=(-10.0, 10.0),
shuffle=True,
random_state=1) # For reproducibility
x =X[:,0]
y =X[:,1]
X=np.c_[x,y]
plt.scatter(x,y,c='white',marker='o',s=50)
plt.grid()
plt.show()
if __name__ == "__main__":
import matplotlib.pyplot as plt
#Exécution du clustering
x_means = XMeans(random_state = 1).fit(np.c_[X])
#Tracez les résultats
plt.rcParams["font.family"] = "Hiragino Kaku Gothic Pro"
plt.scatter(x, y, c = x_means.labels_, s = 30)
plt.scatter(x_means.cluster_centers_[:,0], x_means.cluster_centers_[:,1], c = "r", marker = "*", s = 250)
plt.title("x-means_test2")
plt.grid()
plt.show()

⇒ Ceci est également divisé correctement!
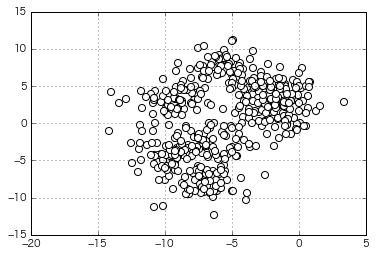
Essayez de regrouper plus de données de mauvaise humeur
(Le nombre de clusters spécifié au moment de la génération est de 8)
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=500,
n_features=2,
centers=8,
cluster_std=1.5,
center_box=(-10.0, 10.0),
shuffle=True,
random_state=1) # For reproducibility
x =X[:,0]
y =X[:,1]
X=np.c_[x,y]
plt.scatter(X[:,0],X[:,1],c='white',marker='o',s=50)
plt.grid()
plt.show()
if __name__ == "__main__":
import matplotlib.pyplot as plt
#Exécution du clustering
x_means = XMeans(random_state = 1).fit(np.c_[X])
#Tracez les résultats
plt.rcParams["font.family"] = "Hiragino Kaku Gothic Pro"
plt.scatter(x, y, c = x_means.labels_, s = 30)
plt.scatter(x_means.cluster_centers_[:,0], x_means.cluster_centers_[:,1], c = "r", marker = "*", s = 250)
plt.title("x-means_test3")
plt.grid()
plt.show()

=> Dans le clustering automatique x-means, le nombre optimal de clusters est calculé comme "5". C'est comme si c'était divisé.
J'essaierai à nouveau d'écrire un livre de coude sans discipline sexuelle
Voir Article précédent pour savoir comment lire le diagramme du coude. (Sortie de la somme des erreurs quadratiques dans les groupes 1 à 10 ensemble)
distortions = []
for i in range(1,11): # 1~Calculez jusqu'à 10 clusters à la fois
km = KMeans(n_clusters=i, #Nombre de clusters
init='k-means++', # k-means++Sélectionnez le centre du cluster par méthode
n_init=10, #K avec différentes valeurs initiales de centroïdes-signifie le nombre d'exécutions par défaut: '10'Sélectionnez le modèle avec la valeur SSE la plus petite comme modèle final
max_iter=300, # k-signifie Nombre maximum d'itérations dans la valeur par défaut de l'algorithme: '300'
random_state=0) #État du générateur de nombres aléatoires utilisé pour initialiser le centroïde
km.fit(X) #Effectuer des calculs de clustering
distortions.append(km.inertia_) # km.fit et km.inertia_Est recherché
y_km = km.fit_predict(X)
plt.plot(range(1,11),distortions,marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.show()

=> Il est encore difficile de juger le nombre optimal de clusters comme "5" à partir de ce chiffre.
J'essaierai à nouveau d'écrire un livre de silhouette sans discipline sexuelle
Voir Article précédent pour savoir comment lire le diagramme de silhouette. (Sortie de tous les diagrammes de silhouette des groupes 3 à 8)
Empruntez le code sur la page officielle scikit-learn Partiellement réécrit)
km = KMeans(n_clusters=5, #Nombre de clusters
init='k-means++', # k-means++Sélectionnez le centre du cluster par méthode
n_init=10, #K avec différentes valeurs initiales de centroïdes-signifie le nombre d'exécutions par défaut: '10'Sélectionnez le modèle avec la valeur SSE la plus petite comme modèle final
max_iter=300, # k-signifie Nombre maximum d'itérations dans la valeur par défaut de l'algorithme: '300'
random_state=0) #État du générateur de nombres aléatoires utilisé pour initialiser le centroïde
y_km = km.fit_predict(X)
from __future__ import print_function
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
print(__doc__)
# Generating the sample data from make_blobs
X, y = make_blobs(n_samples=500,
n_features=2,
centers=8,
cluster_std=1.5,
center_box=(-10.0, 10.0),
shuffle=True,
random_state=1) # For reproducibility
range_n_clusters = [3, 4, 5, 6, 7, 8]
for n_clusters in range_n_clusters:
# Create a subplot with 1 row and 2 columns
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.set_size_inches(18, 7)
# The 1st subplot is the silhouette plot
# The silhouette coefficient can range from -1, 1 but in this example all
# lie within [-0.1, 1]
ax1.set_xlim([-0.1, 1])
# The (n_clusters+1)*10 is for inserting blank space between silhouette
# plots of individual clusters, to demarcate them clearly.
ax1.set_ylim([0, len(X) + (n_clusters + 1) * 10])
# Initialize the clusterer with n_clusters value and a random generator
# seed of 10 for reproducibility.
clusterer = KMeans(n_clusters=n_clusters, random_state=1)
cluster_labels = clusterer.fit_predict(X)
# The silhouette_score gives the average value for all the samples.
# This gives a perspective into the density and separation of the formed
# clusters
silhouette_avg = silhouette_score(X, cluster_labels)
print("For n_clusters =", n_clusters,
"The average silhouette_score is :", silhouette_avg)
# Compute the silhouette scores for each sample
sample_silhouette_values = silhouette_samples(X, cluster_labels,metric='euclidean')
y_lower = 10
for i in range(n_clusters):
# Aggregate the silhouette scores for samples belonging to
# cluster i, and sort them
ith_cluster_silhouette_values = \
sample_silhouette_values[cluster_labels == i]
ith_cluster_silhouette_values.sort()
size_cluster_i = ith_cluster_silhouette_values.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.spectral(float(i) / n_clusters)
ax1.fill_betweenx(np.arange(y_lower, y_upper),
0, ith_cluster_silhouette_values,
facecolor=color, edgecolor=color, alpha=0.7)
# Label the silhouette plots with their cluster numbers at the middle
ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
# Compute the new y_lower for next plot
y_lower = y_upper + 10 # 10 for the 0 samples
ax1.set_title("The silhouette plot for the various clusters.")
ax1.set_xlabel("The silhouette coefficient values")
ax1.set_ylabel("Cluster label")
# The vertical line for average silhoutte score of all the values
ax1.axvline(x=silhouette_avg, color="red", linestyle="--")
ax1.set_yticks([]) # Clear the yaxis labels / ticks
ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
# 2nd Plot showing the actual clusters formed
colors = cm.spectral(cluster_labels.astype(float) / n_clusters)
ax2.scatter(X[:, 0], X[:, 1], marker='.', s=30, lw=0, alpha=0.7,
c=colors)
# Labeling the clusters
centers = clusterer.cluster_centers_
# Draw white circles at cluster centers
ax2.scatter(centers[:, 0], centers[:, 1],
marker='o', c="white", alpha=1, s=200)
for i, c in enumerate(centers):
ax2.scatter(c[0], c[1], marker='$%d$' % i, alpha=1, s=100)
ax2.set_title("The visualization of the clustered data.")
ax2.set_xlabel("Feature space for the 1st feature")
ax2.set_ylabel("Feature space for the 2nd feature")
plt.suptitle(("Silhouette analysis for KMeans clustering on sample data "
"with n_clusters = %d" % n_clusters),
fontsize=14, fontweight='bold')
plt.grid()
plt.show()
Automatically created module for IPython interactive environment
For n_clusters = 3 The average silhouette_score is : 0.500273979793

For n_clusters = 4 The average silhouette_score is : 0.473805434223
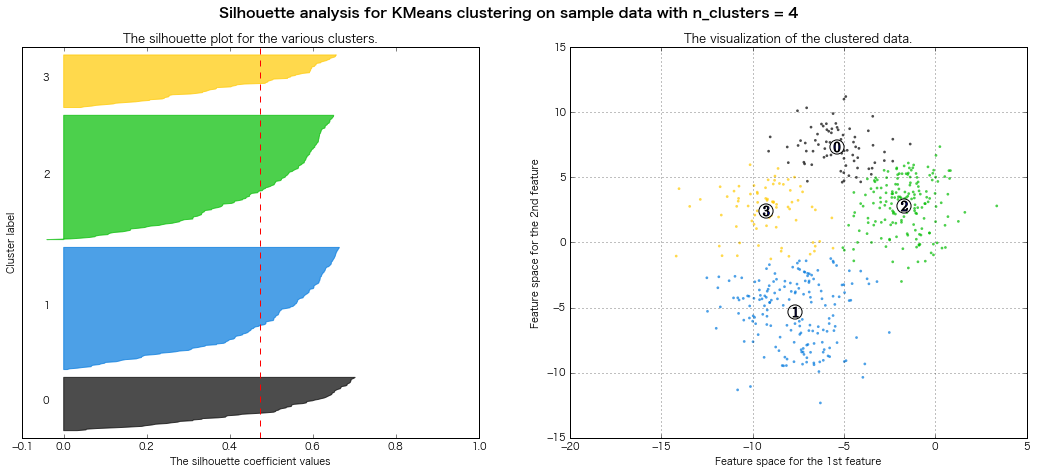
For n_clusters = 5 The average silhouette_score is : 0.451524016461

For n_clusters = 6 The average silhouette_score is : 0.428239776719

For n_clusters = 7 The average silhouette_score is : 0.427688325647
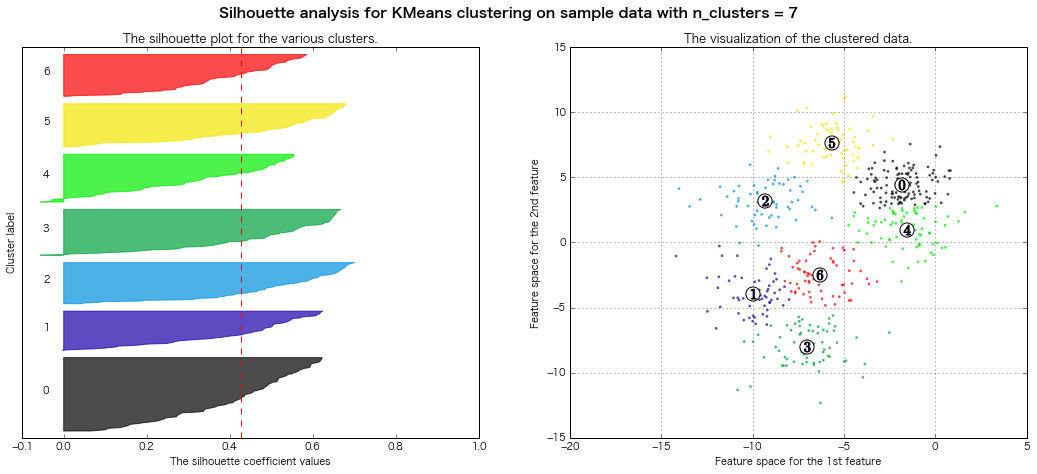
For n_clusters = 8 The average silhouette_score is : 0.409792863353

=> Evaluation du diagramme de silhouette Légalement, il semble que 7 ou 8 grappes soient bonnes.
Conclusion
--x-means semble certainement bien se regrouper «Cependant, il n'y a aucun moyen de« faire correspondre »le nombre de clusters, et pensez-vous que vous allez l'utiliser pour« obtenir une «ligne directrice» pour le nombre optimal de clusters? » ――Il est encore difficile d'obtenir une estimation du nombre optimal de grappes à partir du diagramme du coude ...?
- Idem pour la méthode de la silhouette ...
⇒ Après tout, a-t-on envie de sélectionner un cluster qui donne des résultats faciles à interpréter en fonction de l'objectif du clustering?
Annexe (j'ai recherché diverses choses pour comprendre le contenu)
Examinons la logique de la méthode x-means! → Je ne connais pas la norme de quantité d'information Basian (BIC) → Je ne connais pas correctement l'AIC en premier lieu → La probabilité est après tout, quoi? → Il existe une estimation bayésienne autre que l'estimation la plus probable pour trouver la vraisemblance ... Continuation sans fin à partir de là rasage de yak
"Acutally, my whole life is just one big yak shaving exercise." - Joi Ito
Critère d'information d'Akaike: AIC (critère d'information d'Akaike)
Indicateur de sélection d'un modèle avec le nombre optimal de paramètres
―― Le modèle créé pour certaines données peut être plus compatible avec les données existantes en augmentant les paramètres, mais il tombe dans le surentraînement. «Il est nécessaire de réduire le nombre de paramètres de modélisation pour ne pas tomber dans le surentraînement, mais c'est un problème difficile de réduire effectivement le nombre. --Calculer l'AIC avec un modèle et afficher la ** valeur minimale ** fera souvent une bonne sélection de modèle ―― Puisque l'AIC est composée de la vraisemblance logarithmique du modèle et du nombre de paramètres, le compromis entre précision et complexité peut être bien décrit.
- Le premier terme de l'équation représente le bon ajustement au modèle, et le second terme représente la pénalité pour la complexité du modèle. --Dans le second terme, plus le nombre de paramètres est petit, plus le problème de surajustement peut être évité, il fonctionne donc mieux pour le modèle avec un nombre de paramètres plus petit. ――Même si l'ajustement est bon, un modèle compliqué foiré n'est pas préférable, donc un index qui s'adapte bien et vise un modèle simple «On peut dire qu'un bon modèle peut généralement être sélectionné en calculant l'AIC pour tous les modèles cibles et en sélectionnant le plus petit modèle.
référence:
- Akaike Information Ctiteriion | wikipedia
- Analyse de séries chronologiques II-Évaluation et prédiction future du modèle ARMA (modèle de moyenne mobile auto-renvoyant) | @IT
Critère d'information bayésien (BIC)
- Dans de nombreux cas, une bonne sélection de modèle peut être effectuée si le BIC indique la valeur minimale.
- Par rapport à l'AIC, un indice qui considère la taille et la taille de l'échantillon comme une pénalité pour la complexité du modèle de la section 2. ―― Contrairement à l'AIC, la sélection par ce critère a une cohérence (un grand nombre d'échantillons donne un ordre vrai).
référence:
Bayesian Information Criterion | wikipedia
Différence entre AIC et BIC
--Différence d'objet --Utilisez AIC si vous souhaitez sélectionner un modèle pour améliorer la précision de la prédiction --Utilisez BIC si vous souhaitez connaître la structure à partir de laquelle les données sont générées
- Différence mathématique
- Article de pénalité au paragraphe 2 ―― Dans l'AIC, lorsque la taille de l'échantillon est grande quelle que soit la taille de l'échantillon, le poids du premier terme devient important et un modèle compliqué a tendance à être sélectionné.
- En BIC, la taille de l'échantillon est prise en compte dans les pénalités, donc un modèle plus simple que l'AIC a tendance à être sélectionné.
--Différence dans la stratégie d'estimation des paramètres du modèle
- L'AIC détermine la valeur maximale de la fonction de vraisemblance par estimation du maximum de vraisemblance --BIC détermine la valeur maximale de la fonction de vraisemblance par estimation bayésienne
«Cependant, il n'y a pas de consensus sur le fait qu'il doit être utilisé de cette manière.
référence:
- Akaike Information Amount Standard AIC et Bayes Information Amount Standard BIC | Tell me! Goo
- [Bayes Information Criteria and Its Development-Overview- | ALBERT Official Blog](http://blog.albert2005.co.jp/2016/04/19/%E3%83%99%E3%82%A4% E3% 82% BA% E6% 83% 85% E5% A0% B1% E9% 87% 8F% E8% A6% 8F% E6% BA% 96% E5% 8F% 8A% E3% 81% B3% E3% 81% 9D% E3% 81% AE% E7% 99% BA% E5% B1% 95-% EF% BD% 9E% E6% A6% 82% E8% AA% AC% E7% B7% A8% EF% BD % 9E /)
Examen de la probabilité
Examen de "Quelle était la probabilité en premier lieu?"
La plausibilité du modèle considérée à partir des données obtenues est appelée plausibilité. Source
Le concept de base de la fonction de vraisemblance est de répondre à la question ** "Après avoir échantillonné et observé les données, de quels paramètres proviennent les données?" ** est. Source
La probabilité est comme la probabilité. Cependant, la façon de penser est différente. Pour la probabilité, les paramètres sont fixes et les données changent, mais pour la probabilité, les données sont fixes et les paramètres changent. Source
référence:
- [Statistiques] Qu'est-ce que la vraisemblance? Expliquons graphiquement. | Qiita
- À propos de la probabilité et de la méthode d'estimation la plus probable | Côté ensoleillé!
Quelle est l'estimation la plus probable?
Lorsque la vraisemblance est maximale = Connaître les paramètres (moyenne et variance dans le cas d'une distribution gaussienne) du modèle que vous voulez estimer (distribution de probabilité: essentiellement distribution gaussienne)
Différence entre l'estimation la plus probable et l'estimation bayésienne
| c'est quoi? | Méthode | En d'autres termes | |
|---|---|---|---|
| Estimation la plus probable | Maximiser la probabilitéComment calculer les paramètres | Probabilité seulementEstimer les paramètres avec (ne pas penser à la probabilité antérieure) | Estimer les paramètres en utilisant uniquement la probabilité des données qui viennent d'être acquises |
| Estimation bayésienne | Maximiser la probabilité postérieureComment calculer les paramètres | Pré-probabilité et vraisemblanceEstimer les paramètres en utilisant les deux | Estimer les paramètres en utilisant non seulement les données qui viennent d'être acquises, mais également la pré-probabilité et la post-probabilité |
référence:
- Qui est la probabilité? | MyEnigma
- Différence entre l'estimation bayésienne et l'estimation la plus probable | Conseils techniques
Laquelle dois-je utiliser, l'estimation la plus probable ou l'estimation bayésienne?
- (grosso modo) Les deux sont fondamentalement les mêmes
- La plus grande différence est ** de considérer ou non la "pré-probabilité" **
- L'estimation la plus probable ne tient pas compte de la probabilité a priori (= on peut dire qu'une distribution uniforme est supposée). En d'autres termes, le début est lorsqu'il n'y a aucune information. --Si les probabilités a priori ne sont pas uniformes, les résultats de l'estimation la plus probable et de l'estimation bayésienne sont différents.
- Dans l'estimation bayésienne, si la probabilité a priori optimale peut être définie, une estimation plus précise peut être effectuée.
- L'estimation de Bayes est une estimation qui utilise plus d'informations.
- Le paramètre de pré-probabilité a tendance à être subjectif. Cela semble être le centre de la controverse entre le plus probable et le bayésien
- En particulier, s'il n'y a pas de prédiction à l'avance ou si la distribution a priori optimale n'est pas connue, une distribution a priori appelée "aucune distribution d'information" est utilisée (de nombreux programmes par défaut à aucune distribution d'information).
À propos de l'estimation bayésienne
Un indicateur typique de la pertinence de l'estimation bayésienne est le ** facteur bayésien (BF) ** --BF représente le ** rapport de vraisemblance ** des deux modèles --BF peut être approximé à BIC (norme de quantité d'information Bayes)
- Différence de BIC entre les deux modèles ≒ deux fois la logarithmique de BF (* Notez qu'ils sont différents simplement parce qu'ils sont similaires)
Référence: Facteur Bayes et sélection du modèle | SlideShare
Critères du facteur Bayes
| BF | 2logBF (≒BIC) | Jugement pour M1 par rapport à M0 |
|---|---|---|
| BF<1 | 2logBF<0 | M0 est meilleur |
| 1<BF<3 | 0<2logBF<2 | M1 est à peine mieux |
| 3<BF<12 | 2<2logBF<5 | M1 est meilleur (positif) |
| 12<BF<150 | 5<2logBF<10 | M1 est bien meilleur (fort) |
| 150<BF | 10<2logBF | M1 est très fort |
Avantages et problèmes de l'utilisation du facteur bayésien pour l'évaluation du modèle
■ Avantages
-
Libérez-vous de la malédiction de l'hypothèse nulle
-
Le test traditionnel a une composition «d'hypothèse nulle» et «d'hypothèse opposée» ――Mais s'il s'agit du facteur Bayes, il suffit de comparer "deux modèles indépendants (hypothèse)" --Il n'y a pas besoin d'une "hypothèse nulle"
-
Libre de la malédiction de la distribution normale --L'équation bayésienne incorpore une distribution a priori ―― «La distribution a priori ne doit pas être une distribution normale» → Elle peut être examinée en appliquant un modèle statistique plus flexible ・ ・ ・ L'estimation bayésienne est utilisée
■ Problèmes
- Le facteur de Bayes est le "rapport de probabilité" des deux modèles ――La magnitude de la valeur numérique ne peut être que "Comparez les deux et ce qui est mieux" ――Il est bon de calculer plusieurs indicateurs et de penser au total --Le calcul est difficile ――Cela devient difficile en raison de l'augmentation des paramètres et de la distribution préalable.
Pour d'autres avantages et inconvénients de l'estimation bayésienne, voir ici.
D'autres qui servent d'indice (de référence) pour sélectionner le modèle le plus adapté
-
Critère d'information sur la déviance (DIC)
-
Valeur P post-mortem
-
Le problème avec des indicateurs tels que l'AIC et le BIC est qu'ils ne peuvent pas être appliqués à des modèles singuliers qui incluent des variables latentes. ――Il semble qu'il existe également une quantité d'informations telles que FIC (critère d'information factorisée) et FAB (inférence bayésienne asymptotique factorisée) pour les traiter.
Référence: [Papier] Un bref résumé de l'apprentissage des mélanges hétérogènes | Feces Net Benkei
Recommended Posts