Implémenter l'extension en Python

Aperçu

Dans cet article, nous expliquerons brièvement le corps fini et le corps développé, et implémenterons le corps de Galois $ \ GF (2 ^ 4) \ $ en Python. En plus de cela, nous implémentons également le cryptage ElGamal sur $ \ GF (2 ^ 4) \ $.

À propos du corps fini

L'ensemble suivant d'éléments $ \ p \ $ premiers est le corps fini $ \ \ mathbb {F} _p \ $.

\mathbb{F}_p = \{ 0, 1, \cdots, p-1\}.

L'addition et la multiplication sont définies dans cet ensemble, par exemple, lorsque $ \ p = 5 \ $

2 + 3 = 0, \ \ 1 + 3 = 4,\ \  3 + 4 = 2,\\
2 \times 3 = 1,\ \  1 \times 3 = 3,\ \  3 \times 4 = 2.

Notez que pour $ a, b \ in \ mathbb {F} _p \ $, le calcul suivant est effectué.

a + b \pmod{p},\\
a \times b \pmod{p}.

Le fait est que le nombre d'origine est un nombre premier. Pour l'expliquer en détail, le reste sonne $ \ mathbb {Z} / p \ mathbb {Z} \ $ et $ \ \ mathbb {Z} / n \ mathbb { Faites-les apparaître dans Z} \ $. Cependant, $ p \ $ est un nombre premier et $ n \ $ est un nombre composé non primaire. L'anneau en surplus est un nom difficile, mais il ressemble à ceci:

\mathbb{Z}/p\mathbb{Z} = \{ 0, 1, \cdots, p-1\},\\
\mathbb{Z}/n\mathbb{Z} = \{ 0, 1, \cdots, n-1\}.

L'addition et la multiplication y sont également définies. Alors, écrivons une "table de multiplication" pour $ p = 5, n = 6 \ $.

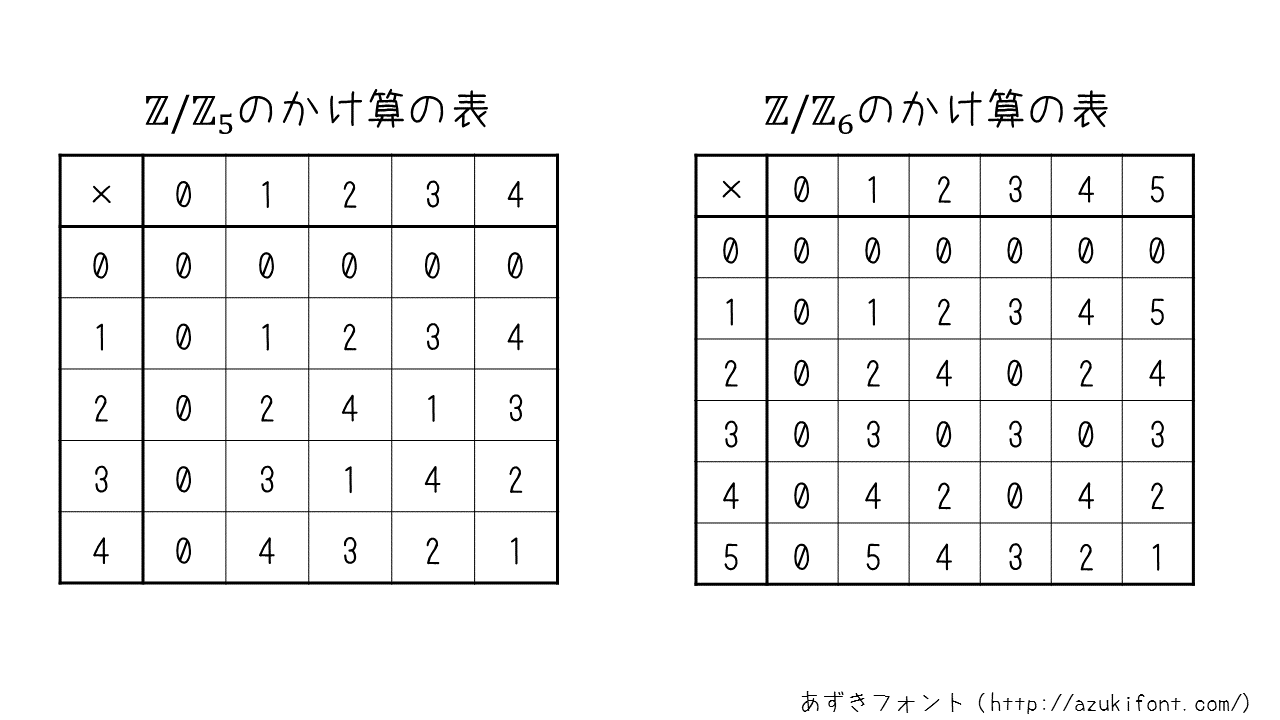
À partir de ce tableau, vous avez peut-être compris la différence entre les deux anneaux résiduels. Autrement dit, dans un anneau de reste dont le nombre d'origine est un nombre premier, le résultat de la multiplication ne sera pas $ \ 0 \ $ à moins que $ 0 \ $ ne soit utilisé. Par conséquent, il n'est pas nécessaire de s'inquiéter du fait que des calculs compliqués tels que la multiplication à plusieurs reprises peuvent rendre des calculs significatifs tels que le cryptage et le décryptage sans signification en raison de l'apparition de $ \ 0 \ $. .. En algèbre, «l'anneau de reste dont le nombre d'origine est un nombre premier» est appelé un «corps fini», ce qui est utile en cryptographie. Par exemple, dans le cas de $ \ mathbb {F} _ {23} \ $

\textbf{a} = \{ 2^j : j\in \{0,1,\cdots, 11\}\}.

À propos du corps élargi

Dans la discussion précédente, si le nombre d'origine était un nombre composé, un corps fini ne pouvait pas être créé. En fait, si $ n = 2 ^ 4 $,

2\times 8 = 0, 4\times4=0.

Cependant, même dans le cas de nombres composites, un corps fini peut être créé en utilisant le polynôme irréductible. Un polynôme irréductible est un polynôme qui ne peut plus être décomposé. Par exemple

x^4 + x +1 est un polynôme contracté,\\
　x^4 + 1　\N'est pas

Parce que chaque coefficient est $ \ \ {0, 1 \} \ $,

x^4 + 1 = x^4 + 2x^2 + 1 = (x^2 + 1)^2.

Maintenant, créons un corps fini. Equations faites avec des polynômes irréductibles: Lorsque la solution de $ x ^ 4 + x + 1 = 0 \ $ est $ \ \ alpha \ $

\textbf{a} = \{ \alpha^j : j\in \{0,1,\cdots, 2^4-2\}\}

Sont toutes des collections originales différentes. Tout d'abord, les quatre éléments suivants sont différents car ils ne peuvent plus être décomposés.

\alpha^0, \alpha^1, \alpha^2, \alpha^3.

D'autres peuvent être confirmés en utilisant $ \ alpha ^ 4 + \ alpha + 1 = 0 \ $.

\alpha^4 = \alpha + 1,\ \alpha^5 = \alpha^2 + \alpha, \ \alpha^6 = \alpha^3 + \alpha^2,\ \alpha^7 = \alpha^3 + \alpha + 1,\\
\alpha^8 = \alpha^2 + 1,\ \alpha^9 = \alpha^3 + \alpha,\ \alpha^{10} = \alpha^2 + \alpha + 1,\ \alpha^{11} = \alpha^3 + \alpha^2 + \alpha,\\
 \alpha^{12} = \alpha^3 + \alpha^2 + \alpha + 1,\ \alpha^{13} = \alpha^3 + \alpha^2 + 1,\ \alpha^{14} = \alpha^3 + 1,\ \alpha^{15}=1.

Comme mentionné ci-dessus, tous les éléments peuvent être représentés par $ \ \ alpha ^ 0, \ alpha ^ 1, \ alpha ^ 2, \ alpha ^ 3 \ $. Si vous considérez les coefficients de $ \ alpha ^ 3, \ alpha ^ 2, \ alpha ^ 1, \ alpha ^ 0 \ $ comme des bits,

\alpha^0 \leftrightarrow 1,\ \alpha^1\leftrightarrow 2,\ \alpha^2\leftrightarrow 4,\ \alpha^3\leftrightarrow 8,\
\alpha^4 \leftrightarrow 3,\ \alpha^5\leftrightarrow 6,\\ \alpha^6\leftrightarrow 12,\ \alpha^7\leftrightarrow 11,\
\alpha^8 \leftrightarrow 5,\ \alpha^9\leftrightarrow 10,\ \alpha^{10}\leftrightarrow 7,\\
\alpha^{11}\leftrightarrow 14,\ \alpha^{12} \leftrightarrow 15, \alpha^{13}\leftrightarrow 13,\ \alpha^{14}\leftrightarrow 9,\ \alpha^{15}\leftrightarrow 1.

Si nous pouvons établir une méthode arithmétique qui consiste en $ \ textbf {a} \ $, nous pouvons réaliser le corps fini $ \ \ mathbb {F} _ {2 ^ 4} \ $.

Implémenter une extension

Le corps galoisien $ \ GF (2 ^ 4) \ $ est adopté comme corps agrandi.

Source et index du corps galoisien GF (16)

Créez l'ensemble d'origine de Galois $ \ GF (2 ^ 4) \ $ $ \ \ textbf {a} = (a_i) \ $ et la table d'index $ \ \ textbf {b} = (b_i) \ $.

 \textbf{a}= \{ 1, 2, 4, 8, 3, 6 , 12, 11, 5, 10, 7, 14, 15, 13, 9, 1\},\\
  \textbf{b}= \{0, 0, 1, 4, 2, 8, 5, 10, 3, 14, 9, 7, 6, 13, 11, 12 \}.

Je m'inquiète pour $ b_0 = 0 \ $, mais peu importe que ce soit $ \ 0 \ $ ou $ \ 100 \ $, mais de toute façon, cela correspond à $ \ a_0 = 1, \ b_1 = 0 \ $. J'espère que tu peux. Autrement dit, $ \ b_0 = 0 \ $ pour plus de commodité. Vous n'avez pas à vous en soucier.

galfield.py

# -*- coding: utf-8 -*-

def galois2(k, l):
    p = pow(2, k)
    a = [1]
    for i in range(p - 1):
        a.append(a[i] * 2)
        if a[i + 1] >= p:
            a[i + 1] = a[i + 1] - p
            a[i + 1] = a[i + 1] ^ l
    return a
 
def table2(a, k):
    b = []
    for i in range(2 ** k):
        b.append(0)
    for i in range(1, 2 ** k):
        for j in range(2 ** k - 1):
            if a[j] == i:
                b[i] = j
    return b
 
 
if __name__ == "__main__":
    # x^4 = x + 1 -> [0, 0, 1, 1] -> ll = 3
    k = 4
    ll = 3
    a = galois2(k, ll)
    b = table2(a, k)

Implémentation de l'arithmétique sur le champ de Galois GF (16)

Une addition

a_i + a_j := a_i \oplus a_j.

Soustraction

a_i - a_j := a_i \oplus a_j.

Multiplier

a_i\times a_j:=a_{b_{a_i}+b_{a_j}} = a_{i + j\pmod{2^4-1}}.

Diviser

a_i / a_j:=a_{b_{a_i}-b_{a_j}} = a_{i - j\pmod{2^4-1}}.

Multiplication de puissance

a_i^n := a_{b_{a_i} \cdot n} = a_{i \cdot n\pmod{2^4-1}}.

Les opérations qui devraient être spécialement mises en œuvre sont la multiplication, la division et la multiplication de puissance.

galois.py

# -*- coding: utf-8 -*-
from galfield import galois2, table2

def gtimes2(k, a, b, s, t):
    return a[(b[s] + b[t]) % (2 ** k - 1)]
 
def gdiv2(k, a, b, s, t):
    return a[(b[s] - b[t]) % (2 ** k - 1)]

def gpow2(k, a, b, s, l):
    return a[(b[s] * l) % (2 ** k - 1)]
 
 
if __name__ == "__main__":
    k = 4
    ll = 3
    a = galois2(k, ll)
    b = table2(a, k)
 
# Example of caluc over galois field
# ADD & SUB
    print a[2] ^ a[5] 
# MUL & DIV
    print gtimes2(k, a, b, a[2], a[5])
    print gdiv2(k, a, b, a[2], a[5])
# POW   
    print gpow2(k, a, b, a[2], 3)

[Annexe] Implémentation du code ElGamal sur l'extension

Le code ElGamal est un code à clé publique proposé par Taher Elgamal d'Egypte en 1984. (Ce n'est pas sécurisé, donc je pense que ce n'est probablement pas pratique ...) Il n'y a pas de signification particulière à implémenter le code ElGamal dans cet article, mais depuis que j'ai implémenté le corps Galois, j'aimerais l'appliquer à quelque chose. Je l'ai écrit ici en annexe parce que j'y ai pensé.

L'algorithme de chiffrement ElGamal est le suivant. (Généralement, l'algorithme de chiffrement à clé publique se compose de trois parties: génération de clé, chiffrement et déchiffrement.) Premièrement, l'ensemble original de Galois $ \ GF (2 ^ 4) $ $ \ \ textbf { Créez a} = (a_i) \ $ et indexez la table $ \ \ textbf {b} = (b_i) \ $.

• Algorithme de génération de clé
  1. x\overset{U}{\leftarrow}\\{ 0, 1, \cdots, 2^4-2\\}.
  2. h\leftarrow a_x.

3. $ x \ $ est la clé privée et $ h \ $ est la clé publique.

• Algorithme de cryptage

1. Sélectionnez le texte brut $ \ m \ in \ textbf {a} \ $.
2. Générez un nombre aléatoire $ \ r \ override {U} {\ leftarrow} \ {0, 1, \ cdots, 2 ^ 4-2 \} \ $.
3. $ c_0 \ leftarrow a_r, \ c_1 \ leftarrow m \ cdot h ^ r \ $ est l'instruction de code.

• Algorithme de décryptage

1. Décrypté par $ c_1 / c_0 ^ x \ rightarrow m \ $.

gElGamal.py

# -*- coding: utf-8 -*-
from random import randint
from galfield import galois2, table2
from galois import gtimes2, gdiv2, gpow2

def GEGKeyGen(a, k):
    sk = randint(0, 2 ** k - 2)
    pk = a[sk]
    return [sk, pk]
 
def GEGEnc(m, a, pk, k):
    r = randint(0, 2 ** k - 2)
    return [a[r], gtimes2(k, a, b, m, gpow2(k, a, b, pk, r))]
 
def GEGDec(c, a, k, sk):
    return gdiv2(k, a, b, c[1], gpow2(k, a, b, c[0], sk))
 
 
if __name__ == "__main__":
    k = 4
    ll = 3
    a = galois2(k, ll)
    b = table2(a, k)
 
    m = a[2]
    key = GEGKeyGen(a, k)
    sk = key[0]
    pk = key[1]
    cipher = GEGEnc(m, a, pk, k)
    print m == GEGDec(cipher, a, k, sk) 

Pour implémenter d'autres extensions ...

J'espère trouver le polynôme irréductible. Par exemple, dans AES du chiffrement à clé commune, $ \ GF (2 ^ 8) \ $ est utilisé, mais son polynôme réciproque est $ \ x ^ 8 + x ^ 4 + x ^ 3 + x ^ 2 + 1 \ $. est. De plus, puisque les bits utilisés dans la somme logique exclusive de galois2 () sont $ [0, 0, 0, 1, 1, 1, 0, 1] $, k = 8, ll = 29 in galfield.py. Vous pouvez exprimer $ \ GF (2 ^ 8) \ $ en définissant . Si vous pouvez comprendre jusqu'à présent, je pense que vous pouvez implémenter d'autres extensions par vous-même.