Pourquoi l'entropie croisée est-elle utilisée pour la fonction objective du problème de classification?

Qu'est-ce qu'un problème de classification?

Le problème de classification classe les données en plusieurs catégories et est l'une des méthodes typiques d'apprentissage automatique.

Prenons l'exemple d'un site d'achat. Prédire si un utilisateur achètera ou non un nouveau produit à partir des informations d'achat d'un utilisateur. La classification en deux catégories (classes) est appelée classification binaire.

Les prédictions de classification avec plus de deux classes sont appelées classification multi-classes. Le jugement des objets dans l'image (reconnaissance d'image) est également l'un des problèmes de classification multi-classes. C'est aussi un problème de classification de juger qu'il s'agit d'un chat basé sur l'image du chat.

Entropie croisée

Deux distributions de probabilité

P(x):Corriger la distribution des données\\
Q(x):Distribution du modèle prédictif

En revanche, l'entropie croisée est définie ci-dessous.

L = - \sum_{x} P(x) \log{Q(x)}

Plus les deux distributions de probabilité sont similaires, plus l'entropie croisée est petite. Utilisant les propriétés de cette fonction, elle est souvent adoptée comme fonction objective dans l'apprentissage automatique (en particulier les problèmes de classification).

Dans cet article, nous examinerons mathématiquement pourquoi l'entropie croisée est souvent adoptée pour les fonctions objectives.

Ce qui suit a été utile pour une explication détaillée de l'entropie croisée. http://cookie-box.hatenablog.com/entry/2017/05/07/121607

Distribution binaire (distribution de Bernouy)

En considérant le problème de classification, prenez la distribution binaire, qui est la distribution de probabilité la plus simple, comme exemple.

P(x_1) = p \;\;\; P(x_2) = 1 - p \\
Q(x_1) = q \;\;\; Q(x_2) = 1 - q \\

Il y a deux boules de couleur, rouge et blanche, dans la boîte, et la probabilité de dessiner du rouge est

P(rouge) = p

La probabilité de dessiner du blanc

P(blanc) = 1 - p

C'est facile à comprendre si on y pense. Si vous avez un total de 10 balles, 2 rouges et 8 blanches

P(rouge) = 0.2 \quad P(blanc) = 0.8

à propos de ça.

Maintenant, à ce moment, la fonction objectif est

\begin{align}
L &= - \sum_{x} P(x) \log{Q(x)} \\
  &= - p \log{q} - (1-p) \log{(1-q)}
\end{align}

Peut être étendu.

Considérez le réseau neuronal simple suivant. Imaginez un scénario où vous voulez enfin trouver la distribution de probabilité $ q $. Pour donner l'exemple précédent, je ne connais pas du tout le contenu de la boîte, mais je vais utiliser certaines données d'entrée pour construire une distribution de probabilité qui dessine une boule rouge comme modèle et prédire le résultat.

y = \sum_{i} x_i w_i \\
\\
q(y) = \frac{1}{1+e^{-y}} :Fonction Sigmaid

Ici, $ x_i $ est une entrée, $ w_i $ est pondérée, $ y $ est une valeur intermédiaire et $ q $ est une sortie. La fonction sigmoïde la plus typique est utilisée comme fonction d'activation.

Formation sur les réseaux neuronaux

Entraînez votre réseau de neurones en trouvant les valeurs des paramètres qui minimisent la valeur de la fonction objectif. Il utilise l'un des algorithmes d'optimisation, ** descente de gradient **.

w \leftarrow w - \eta \frac{\partial L}{\partial w}

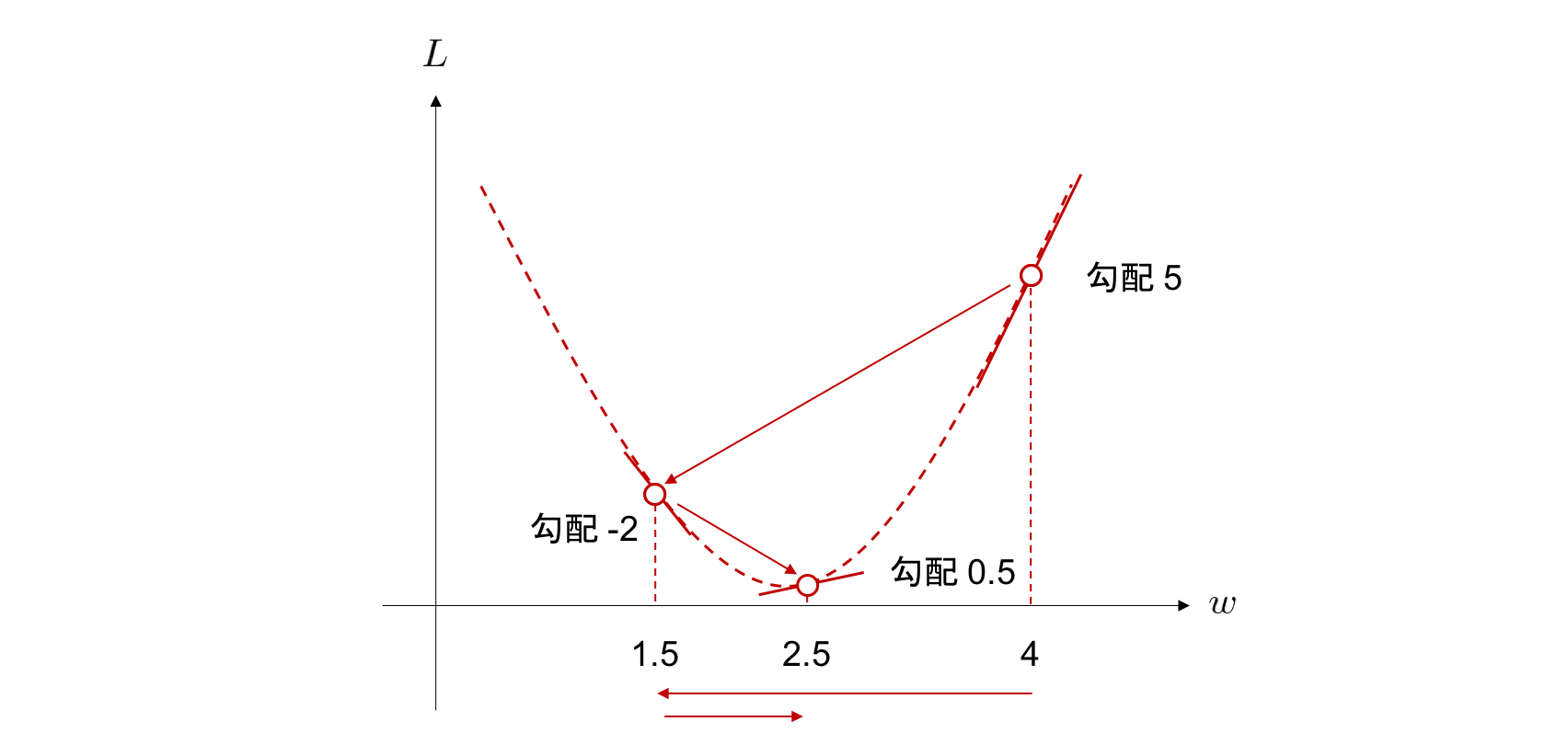
La méthode de descente de gradient est une méthode de calcul répété du ** taux d'apprentissage × gradient de la fonction objectif ** pour trouver le poids qui prend la valeur minimale de la fonction objectif.

Le tutoriel Chainer suivant est très facile à comprendre pour une explication détaillée de ce domaine. https://tutorials.chainer.org/ja/13_Basics_of_Neural_Networks.html

Différencions la fonction objectif à la fois.

\frac{\partial L }{\partial w_i} = \frac{\partial y}{\partial w_i} \frac{\partial q }{\partial y}\frac{\partial L }{\partial q}

La première différenciation est

\frac{\partial y}{\partial w_i} = \frac{\partial}{\partial w_i} \sum_i x_i w_i = x_i

La deuxième différenciation est

\begin{align}
\frac{\partial q }{\partial y} &= \frac{\partial}{\partial y} \frac{1}{1+e^{-y}} \\
&= \frac{\partial u}{\partial y}\frac{\partial}{\partial u} \frac{1}{u} \\
&= -e^{-y} (-u^{-2}) \\
&= \frac{e^{-y}}{1+e^{-y}}\frac{1}{1+e^{-y}} \\
&= \bigl( \frac{1+e^{-y}}{1+e^{-y}} - \frac{1}{1+e^{-y}} \bigr) \frac{1}{1+e^{-y}} \\
&= \bigl( 1-q(y) \bigr) q(y)
\end{align}

La troisième différenciation est

\begin{align}
\frac{\partial L}{\partial q} &= \frac{\partial}{\partial q} \{ - p \log{q} - (1-p) \log{(1-q)} \} \\
&= - \frac{p}{q} + \frac{1-p}{1-q}

\end{align}

Parce qu'il peut être calculé

\frac{\partial L }{\partial w_i} = x_i (1-q) q \bigl( - \frac{p}{q} + \frac{1-p}{1-q} \bigr) = x_i (q-p)

En d'autres termes

p = q

Quand est, la fonction objectif prend la valeur minimale. En d'autres termes, cela signifie que la distribution des données correctes et la distribution du modèle de prédiction sont exactement les mêmes.

Eh bien, je dis juste la chose évidente. Il y a en fait 8 rouges et 2 blancs dans la boîte Il prédit que le rouge est à 80% et le blanc à 20%.

Appliquer aux problèmes de classification

Maintenant, augmentons un peu plus la variation en tant que problème de classification. Par exemple, dans un problème de classification, les catégories peuvent être représentées par 0, 1.

pomme: [1, 0, 0]
Gorira: [0, 1, 0]
Rappa: [0, 0, 1]

Si c'est un peu plus généralisé

La bonne réponse pour la classe à laquelle appartient x est

t=[t_1, t_2 …t_K]^T

Donné dans le vecteur. Cependant, supposons que ce vecteur soit tel qu'un seul de $ t_k ; (k = 1,2,…, K) $ est 1 et les autres sont 0. C'est ce qu'on appelle un vecteur à 1 chaud.

Maintenant que nous pouvons définir le problème de classification de cette manière, la fonction objectif ressemble à ceci:

L = - \sum_x P(x) \log{ Q(x) } = - \log{ Q(x) }

$ Q (x) $ représente la probabilité que les données de formation soient les mêmes que les données de l'enseignant. Tracons-le.

Dans la méthode de descente de gradient, le poids $ w_i $ qui minimise la fonction objectif est obtenu en calculant à plusieurs reprises le ** taux d'apprentissage × gradient de la fonction objectif **. Si le ** taux d'apprentissage ** est extrêmement élevé, ou si le ** gradient de fonction objectif ** est grand, l'efficacité d'apprentissage semble bonne. Cela réduit également le nombre d'étapes de calcul.

On voit que pour $ 0 <Q (x) <1 $, la fonction objectif $ L $ décroît brusquement près de $ Q (x) = 0 $. À partir de là, si les données de l'enseignant et le résultat d'apprentissage sont trop différents, on peut interpréter que la quantité de diminution par étape est importante. Dans le problème de classification, si vous sélectionnez l'entropie croisée comme fonction objectif, l'efficacité du calcul est bonne.

Il est facile d'oublier si vous utilisez réellement une bibliothèque comme Chainer ou Pytorch. Il est également bon de revenir sur la théorie de base pour ne pas l'oublier. J'ai beaucoup appris.

référence https://mathwords.net/kousaentropy https://water2litter.net/rum/post/ai_loss_function/ http://yaju3d.hatenablog.jp/entry/2018/11/30/225841 https://avinton.com/academy/classification-regression/