Cet article présente l'un des modèles d'apprentissage en profondeur, le Variational Autoencoder (VAE). J'essaye d'utiliser Chainer comme cadre d'apprentissage en profondeur.

Avec VAE, vous pouvez créer des images comme celle-ci. VAE est l'un des modèles de génération par apprentissage en profondeur, et il est possible de générer des données similaires à l'ensemble de données d'apprentissage en capturant ses caractéristiques en fonction des données d'apprentissage. Vous trouverez ci-dessous une version animée des données générées par VAE. Veuillez consulter le texte pour plus de détails.

Le code Python introduit dans cet article peut être trouvé à ici.

1. Qu'est-ce que l'autoencodeur variationnel?

Tout d'abord, je voudrais expliquer ce qu'est la VAE, mais avant cela, je voudrais parler d'un encodeur automatique normal.

1-1. Codeur automatique normal

Qu'est-ce qu'un encodeur automatique?

Un apprentissage non supervisé. Par conséquent, les données d'entrée au moment de l'apprentissage ne sont que des données de formation, pas des données d'enseignant.
Un réseau neuronal pour acquérir des fonctionnalités qui représentent des données.

Il a de telles caractéristiques. Prenant MNIST comme exemple, c'est un réseau neuronal qui met une image de nombres 28x28 et produit la même image. C'est une image de la figure ci-dessous. Le réseau neuronal qui convertit les données d'entrée $ X $ en la variable latente $ z $ est appelé Encoder. (Il est nommé Encoder car les données d'entrée peuvent être considérées comme codées.) À ce stade, si la dimension de $ z $ est plus petite que l'entrée $ X $, elle peut également être considérée comme une réduction de dimension. Inversement, un réseau neuronal qui restaure l'image d'origine en utilisant la variable latente $ z $ comme entrée est appelé un décodeur.

Lorsque le cas où le réseau neuronal a une couche est exprimé par une formule mathématique,

\hat{x}(x) = \hat{f}(\hat{W} f(Wx+b)+\hat{b})

est. Perte à ce moment

Loss = \sum_{n=1}^N \|x_n - \hat{x}(x_n) \|^2

ça ira. C'est ce qu'on appelle une erreur de reconstruction. Il peut être appris en mettant à jour les poids par la méthode de propagation de retour d'erreur afin qu'il soit aussi proche que possible des données d'entrée.

1-2. Variational Autoencoder(VAE) La grande différence est que VAE suppose une distribution de probabilité pour cette variable latente $ z $, généralement $ z \ sim N (0, 1) $. Avec un encodeur automatique normal, je pousse des données dans la variable latente $ z $, mais je ne suis pas sûr de la structure. VAE permet de pousser la variable latente $ z $ dans une structure appelée distribution de probabilité. L'image est ci-dessous. Variational Autoencoder

Je ne suis pas encore sûr. Si vous regardez ce que vous exécutez réellement le programme, vous obtiendrez une petite image. Tout d'abord, comparons l'entrée et la sortie. (Cela a été appris en définissant la dimension de $ z $ sur 20.) C'est un peu vague, mais la forme d'origine est presque restaurée. Puisque MNIST est à l'origine des données de 784 dimensions, on peut dire que la plupart des caractéristiques essentielles pourraient être incorporées dans la dimension réduite de 20 dimensions.

Ensuite, voyons le comportement uniquement dans la partie Encoder. En supposant qu'il existe un encodeur qui a déjà été entraîné, placez-y un ensemble de données de formation et déposez-le dans une variable latente. Rendez la dimension $ z $ bidimensionnelle pour qu'elle puisse être visualisée. Vous pouvez voir que l'ensemble de données MNIST de données d'entraînement est dispersé sur un cercle qui suit une distribution normale bidimensionnelle. De plus, bien qu'il s'agisse d'un miso, on peut voir que les données portant le même libellé de classe sont rassemblées à proximité malgré un apprentissage non supervisé sans données sur les enseignants. En effet, VAE est conçu pour que $ z $ suive une distribution normale et incorpore des nombres aléatoires qui suivent la distribution normale pendant l'apprentissage, de sorte que ce flou aléatoire a pour effet de rapprocher des formes similaires. En d'autres termes, même si vous entrez la même image, $ z $ sera tracé à une position légèrement différente à chaque fois, et l'image générée par Decoder à partir de ce $ z $ sera la même que l'image d'entrée. La position où les nombres sont tracés dans le texte dans le diagramme de dispersion ci-dessous est au centre de chaque étiquette. Encoder

Maintenant, que se passe-t-il si nous essayons de générer des données en déplaçant progressivement les données de «0» à «7» le long de l'espace de la variable latente?

L'animation ci-dessous est le résultat.

t\cdot z_0 + (1-t)\cdot z_7, \ \ 0\leq t \leq 1

L'image MNIST est générée par Decoder avec $ t $ déplacé de 0 à 1 petit à petit en entrée. Vous pouvez voir comment il commence à partir de 0 et passe par les nombres entre 0-6-2-8-9-4-7 et 7: wink: Ce sont N (0), pas les données d'entraînement elles-mêmes. , 1) Le miso est que l'image est générée par VAE mappée ci-dessus.

Vous trouverez ci-dessous un affichage de chaque image.

La figure ci-dessous montre l'image de sortie correspondante en découpant $ -2 \ leq z_1 \ leq 2, \ -2 \ leq z_2 \ leq 2 $ de l'espace bidimensionnel de $ z $ et en l'introduisant dans le décodeur. Devenir. La ligne rouge est la trajectoire du mouvement précédent.

À partir des données d'apprentissage, on peut voir que la relation de position est presque la même que la carte $ z $ générée par Encoder. Au contraire, l'endroit où la probabilité (densité) est très faible du point de vue de N (0, 1) est éloigné de l'ensemble de données d'origine, de sorte que l'image générée correspondante est brisée sous forme de nombres. On peut dire que cela représente correctement la structure de la distribution de probabilité de la génération de données.

C'est un diagramme montrant toutes les situations qui commencent de 0 à 9 et atteignent chacune de 0 à 9. Cet exemple augmente la dimension de la variable latente à 20. Donc, contrairement à avant, il y a moins de numéros en cours de route. Puisque la dimension est élevée, le pouvoir d'expression s'est amélioré.

1-3. Hypothèse de la diversité

L'une des fonctionnalités de Deep Learning est que vous pouvez combiner l'apprentissage des tâches et l'apprentissage des expressions. Les données de haute dimension telles que les images ne sont en fait distribuées que dans une petite partie des données de haute dimension, et les données significatives (données qui capturent l'essence des données d'entraînement) se trouvent dans les données de haute dimension. Il existe une hypothèse multiple qui est considérée comme solidifiée localement. Je pense que l'exemple des données sur les rouleaux suisses ci-dessous est facile à comprendre. Les données sont réparties sur trois dimensions, mais les données sont assez localement biaisées, et vous pouvez voir que la plupart des données peuvent en fait être représentées en deux dimensions. Il y a un espace sans données entre les rouleaux. Par conséquent, les données proches en trois dimensions ne sont pas toujours similaires et il est plus probable que des données similaires soient trouvées en considérant la distance en se déplaçant dans la direction le long de la phase. Il vaut donc mieux l'ouvrir en deux dimensions et mesurer la distance.

[Le rouleau suisse en tant que multidimensionnel bidimensionnel en trois dimensions]
[Lorsque vous développez le rouleau suisse en deux dimensions, il ressemble à ceci]

Revenant à la VAE de MNIST de Swissroll, VAE capture cette variété et la pousse de la dimension de données d'image MNIST à 784 dimensions à la variable latente $ z \ sim N (0, 1) $ dimension. Voir aussi [7] pour l'apprentissage d'expression et l'hypothèse de diversité.

2. Mise en œuvre avec Chainer

J'expliquerai en utilisant une version personnalisée basée sur Exemple officiel de Chainer. L'encodeur et le décodeur sont modélisés à l'aide de MLP (Multi Layer Perceptron) à 3 couches.

Le graphique de calcul généré par Chainer avant le code est illustré ci-dessous. Vous pouvez voir que le MLP fait partie des trois couches de l'encodeur et du décodeur et l'utilisation de Gaussian, c'est-à-dire un nombre aléatoire qui suit une distribution normale, pour générer la variable latente $ z $. L'encodeur exprime $ z $ en sortant les paramètres $ \ mu $ et $ \ sigma ^ 2 $ de cette distribution normale.

# Reference: https://jmetzen.github.io/2015-11-27/vae.html
class Xavier(initializer.Initializer):
    """
    Xavier initializaer 
    Reference: 
    * https://jmetzen.github.io/2015-11-27/vae.html
    * https://stackoverflow.com/questions/33640581/how-to-do-xavier-initialization-on-tensorflow
    """
    def __init__(self, fan_in, fan_out, constant=1, dtype=None):
        self.fan_in = fan_in
        self.fan_out = fan_out
        self.high = constant*np.sqrt(6.0/(fan_in + fan_out))
        self.low = -self.high
        super(Xavier, self).__init__(dtype)

    def __call__(self, array):
        xp = cuda.get_array_module(array)
        args = {'low': self.low, 'high': self.high, 'size': array.shape}
        if xp is not np:
            # Only CuPy supports dtype option
            if self.dtype == np.float32 or self.dtype == np.float16:
                # float16 is not supported in cuRAND
                args['dtype'] = np.float32
        array[...] = xp.random.uniform(**args)


# Original implementation: https://github.com/chainer/chainer/tree/master/examples/vae
class VAE(chainer.Chain):
    """Variational AutoEncoder"""

    def __init__(self, n_in, n_latent, n_h, act_func=F.tanh):
        super(VAE, self).__init__()
        self.act_func = act_func
        with self.init_scope():
            # encoder
            self.le1        = L.Linear(n_in, n_h,      initialW=Xavier(n_in, n_h))
            self.le2        = L.Linear(n_h,  n_h,      initialW=Xavier(n_h, n_h))
            self.le3_mu     = L.Linear(n_h,  n_latent, initialW=Xavier(n_h,  n_latent))
            self.le3_ln_var = L.Linear(n_h,  n_latent, initialW=Xavier(n_h,  n_latent))
            
            # decoder
            self.ld1 = L.Linear(n_latent, n_h, initialW=Xavier(n_latent, n_h))
            self.ld2 = L.Linear(n_h,      n_h, initialW=Xavier(n_h, n_h))
            self.ld3 = L.Linear(n_h,      n_in,initialW=Xavier(n_h, n_in))

    def __call__(self, x, sigmoid=True):
        """ AutoEncoder """
        return self.decode(self.encode(x)[0], sigmoid)

    def encode(self, x):
        if type(x) != chainer.variable.Variable:
            x = chainer.Variable(x)
        x.name = "x"
        h1 = self.act_func(self.le1(x))
        h1.name = "enc_h1"
        h2 = self.act_func(self.le2(h1))
        h2.name = "enc_h2"
        mu = self.le3_mu(h2)
        mu.name = "z_mu"
        ln_var = self.le3_ln_var(h2)  # ln_var = log(sigma**2)
        ln_var.name = "z_ln_var"
        return mu, ln_var

    def decode(self, z, sigmoid=True):
        h1 = self.act_func(self.ld1(z))
        h1.name = "dec_h1"
        h2 = self.act_func(self.ld2(h1))
        h2.name = "dec_h2"
        h3 = self.ld3(h2)
        h3.name = "dec_h3"
        if sigmoid:
            return F.sigmoid(h3)
        else:
            return h3

    def get_loss_func(self, C=1.0, k=1):
        """Get loss function of VAE.

        The loss value is equal to ELBO (Evidence Lower Bound)
        multiplied by -1.

        Args:
            C (int): Usually this is 1.0. Can be changed to control the
                second term of ELBO bound, which works as regularization.
            k (int): Number of Monte Carlo samples used in encoded vector.
        """
        def lf(x):
            mu, ln_var = self.encode(x)
            batchsize = len(mu.data)
            # reconstruction error
            rec_loss = 0
            for l in six.moves.range(k):
                z = F.gaussian(mu, ln_var)
                z.name = "z"
                rec_loss += F.bernoulli_nll(x, self.decode(z, sigmoid=False)) / (k * batchsize)
            self.rec_loss = rec_loss
            self.rec_loss.name = "reconstruction error"
            self.latent_loss = C * gaussian_kl_divergence(mu, ln_var) / batchsize
            self.latent_loss.name = "latent loss"
            self.loss = self.rec_loss + self.latent_loss
            self.loss.name = "loss"
            return self.loss
        return lf

3. Aperçu théorique de la VAE

Le but du modèle généré est d'estimer la distribution des données, $ p (X) $. Dans les termes de PRML, c'est comme suit.

L'approche de modélisation de la distribution des entrées ainsi que de la distribution des sorties implicitement ou explicitement est appelée le ** modèle génératif ** car il peut générer des données artificielles dans l'espace d'entrée en échantillonnant à partir du modèle. " PRML Volume 1 p42)

Lorsqu'on considère les images, $ X $ est généralement des données de très grande dimension. Étant donné que cet article cible MNIST, il s'agit de données de 784 dimensions. Comme présenté dans la section précédente, il y a très peu d'endroits dans cette dimension supérieure où les données existent réellement, nous les avons donc bien capturées ainsi que la variable latente $ z du facteur de dimension inférieure (par exemple, 10e dimension). Pensez à l'exprimer avec $. En d'autres termes, nous essayons de construire une correspondance entre les données de haute dimension $ X $ et les données de faible dimension $ z $ et de bien l'utiliser. VAE entraîne cette variable latente $ z $ à être distribuée comme une distribution normale et estime $ p (X) $. $ p (X) $ est parfois appelé preuve.

ici,

$ p (\ cdot) $: modèle de probabilité
$ z $: variable latente
$ X $: Données

ça ira. Étant donné que cette distribution de probabilité a des paramètres, la méthode la plus probable pour $ p (X) $ peut être utilisée pour trouver le paramètre pour $ p (X) $ qui représente le mieux $ X $. En VAE, un réseau de neurones est utilisé pour certains des éléments qui composent cette distribution de probabilité, et ses paramètres sont obtenus par la méthode de propagation des erreurs et la méthode de descente de gradient stochastique.

Le modèle graphique montre la relation entre la variable latente $ z $ et les données $ X $.

Le réseau neuronal qui associe la variable latente $ z $ aux données $ X $ est appelé Encoder. Si vous pensez à l'analogie de la compression de fichier image comme le soi-disant jpeg, vous pouvez voir pourquoi il s'appelle Encoder. encoder

Inversement, Decoder est un réseau neuronal qui restaure les données $ X $ à partir de la variable latente $ z $. decoder

D'après ce qui précède, la VAE constituée d'un codeur, d'un décodeur et de deux réseaux neuronaux peut être modélisée comme suit. $ \ phi $ est le paramètre Encoder et $ \ theta $ est le paramètre Decoder. Le fait est que Encoder ne génère pas directement $ z $, mais plutôt les paramètres normalement distribués $ \ mu, \ sigma $ que $ z $ suit, comme indiqué ci-dessous.

Nous avons déterminé que le modèle $ p (X) $ que nous voulons estimer est un modèle constitué de deux réseaux de neurones comme décrit ci-dessus. Le reste est la procédure pour trouver les paramètres qui correspondent aux données. En considérant les étapes ci-dessous, nous pouvons voir que nous devrions trouver le paramètre qui maximise la limite inférieure variationnelle $ L (X, z) $ (décrite plus loin). La limite inférieure de variation est parfois appelée ELBO (Evidence Lower BOund).

** Étapes de réflexion sur la recherche de paramètres **

Trouvez les paramètres de réseau neuronal $ \ theta, \ phi $ qui maximisent la probabilité de $ p (X) $ par la méthode la plus probable.
Cible pour maximiser la vraisemblance du journal $ \ log p (X) $ pour en faciliter l'utilisation.
Puisqu'il est difficile de gérer l'intégration en maximisant $ \ log p (X) $ tel quel, en maximisant la limite inférieure de variation $ L (X, z) $ et en partant du bas pour la supprimer Trouvez le paramètre qui maximise le degré.

Quelle est la limite inférieure de cette variation? Ceci est calculé comme suit.

Veuillez également consulter [ici](http://qiita.com/kenmatsu4/items/26d098a4048f84bf85fb) pour l'inégalité de Jensen.

En raison de l'inégalité, $ L (X, z) $ représente la limite inférieure de $ \ log p (X) $, et il y a un espace comme représenté par le "?" Dans la figure ci-dessous.

Enregistrez la probabilité de trouver ce "?"\log p(X)Et la limite inférieure de variationL(X, z)Lors du calcul de la différence entre, à partir de la formule suivanteD_{KL}[q(z|X) \| p(z|X)]Tu peux voir ça.

Dans la dernière formule, il est supérieur ou égal à 0 car la divergence de Calback Libra est toujours supérieure ou égale à 0.

Par conséquent, la limite inférieure de variation est

est devenu. Puisque le premier terme est une valeur fixe et le second terme est un élément dépendant du paramètre, la «maximisation de la limite inférieure de variation» cible est la divergence de Calback Libra.D_{KL}[q_{\phi}(z|X) || p_{\theta}(z|X)]Équivaut à la minimisation de.

Cette divergence de Calback BalanceD_{KL}[q_{\phi}(z|X) || p_{\theta}(z|X)]Peut être décomposé en trois termes comme indiqué ci-dessous.

Remplacez-le dans l'équation de la borne inférieure de la variation.

Nous savons maintenant que la limite inférieure de variation peut être exprimée par deux termes.

Le deuxième élément est\mathbf{E}_{q(z|X)}[\log p(X|z)]Et cela signifie Encoder, Decoder. En d'autres termesq(z|X)Données surXConsigner la probabilité de\log p(X|z)Je souhaite maximiser la valeur attendue de. Inféré par Encoder à la distribution de probabilitézConsigner la probabilité en utilisant la distribution de\log p(X|z)Je prends la valeur attendue de. Voici la partie pertinente de Chainer.

            mu, ln_var = self.encode(x)
            batchsize = len(mu.data)
            # reconstruction error
            rec_loss = 0
            for l in six.moves.range(k):
                z = F.gaussian(mu, ln_var)
                z.name = "z"
                rec_loss += F.bernoulli_nll(x, self.decode(z, sigmoid=False)) / (k * batchsize)

Supposons que $ p_ {\ theta} (X | z) $ suit une distribution de Bernoulli multivariée (de [3] C.1 Bernoulli MLP comme décodeur) [F.bernoulli_nll](https://docs.chainer.org/ La perte est calculée avec en / stable / reference / generated / chainer.functions.bernoulli_nll.html # chainer.functions.bernoulli_nll). En d'autres termes, en supposant que chaque pixel prend une valeur comprise entre 0 et 1, on considère que la sortie de VAE et l'image d'entrée ont une entropie croisée. Cette perte s'appelle l'erreur de reconstruction.

Premier élémentD_{KL}[q(z|X) \| p(z)]Est un terme de régularisation,zLa distribution estp(z)En d'autres termesN(0, I)C'est un terme contraint d'être.q(z|X)Quandp(z)La distribution est近づけば近づくほどカルバックライブラーダイバージェンスの値は0に近づくので、変分下限が大きくなるこQuandになります。 Voici la partie pertinente de Chainer.

self.latent_loss = C * gaussian_kl_divergence(mu, ln_var) / batchsize

La partie centrale de «la division_kl_gaussienne» est la suivante.

    var = exponential.exp(ln_var)
    mean_square = mean * mean
    loss = (mean_square + var - ln_var - 1) * 0.5

Il calcule la divergence Calback Libra en suivant une distribution normale. (Voir [3] APPENDICE B) latent_loss

(Pour la dérivation de Kullback Leibler Divergence dans le cas d'une distribution normale, veuillez vous référer à l'article de commentaire ici.)

Vous pouvez maintenant calculer ce que vous souhaitez maximiser. Puisque l'apprentissage du réseau de neurones est effectué avec la valeur de minimiser la perte, les paramètres $ \ theta et \ phi $ sont optimisés en multipliant la limite inférieure de la variation par moins comme fonction de perte.

Reparameterization Trick

Le dernier problème est que dans la structure précédente, il y a une distribution de probabilité de $ z \ sim N (\ mu (X), \ sigma (X)) $ entre les deux, donc la méthode de propagation des erreurs est utilisée. Il ne sera pas possible de postuler ci-dessous. Une technique appelée Reparameterization Trick est utilisée pour résoudre ce problème. Au lieu de traiter directement avec $ z \ sim N (\ mu (X), \ sigma (X)) $, générez du bruit à $ \ varepsilon \ sim N (0, I) $ et $ z = \ mu En se connectant sous la forme de (X) + \ varepsilon * \ sigma (X) $, VAE est construite comme le montre la figure ci-dessous, en évitant les variables stochastiques et en suivant la flèche bleue à l'envers, en appliquant la méthode de propagation de l'erreur. C'est quelque chose à faire.

En termes de code Chainer, ce qui suit est applicable.

            mu, ln_var = self.encode(x)
            batchsize = len(mu.data)
            # reconstruction error
            rec_loss = 0
            for l in six.moves.range(k):
                z = F.gaussian(mu, ln_var)

prime

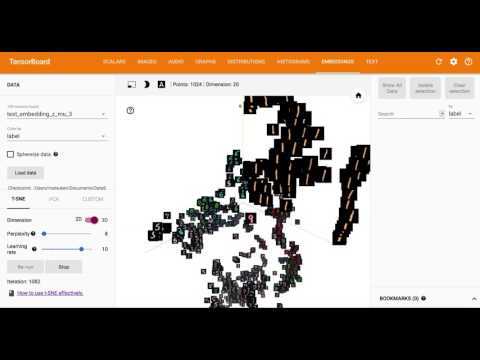
En utilisant Embedding, l'une des fonctions de Tensorboard de TensorFlow, la variable latente à 20 dimensions $ z $ est visualisée en la réduisant en 3D et 2D avec T-SNE.

référence

[1] Code Python pour cet article 　https://github.com/matsuken92/Qiita_Contents/tree/master/chainer-vae

[2] Tutorial on Variational Autoencoders 　https://arxiv.org/abs/1606.05908

[3] Auto-Encoding Variational Bayes(Diederik P Kingma, Max Welling) 　https://arxiv.org/abs/1312.6114

[4] Méthode de Bayes pour le traitement du langage naturel (Daichi Mochihashi) 　http://chasen.org/~daiti-m/paper/vb-nlp-tutorial.pdf

[5] Codeur automatique variationnel (Sho Tatsuno) que même les chats peuvent comprendre 　https://www.slideshare.net/ssusere55c63/variational-autoencoder-64515581

[6] Deep Learning (Seiya Tokui) du modèle généré 　https://www.slideshare.net/beam2d/learning-generator

[7] Apprentissage des expressions par le modèle de génération profonde IIBMP2016 　https://www.slideshare.net/pfi/iibmp2016-okanohara-deep-generative-models-for-representation-learning

[8] Variational AutoEncoder 　https://www.slideshare.net/KazukiNitta/variational-autoencoder-68705109

[9] Deep Learning Chapter 17 The Manifold Perspective on Representation Learning 　http://www.deeplearningbook.org/version-2015-10-03/contents/manifolds.html

Autoencoder variationnel Explication approfondie