Apprenez les méthodes M-H et HMC en lisant les statistiques bayésiennes à partir des bases
Introduction (pourquoi avez-vous choisi cela)
L'échantillonnage est l'une des méthodes adoptées dans les situations où le calcul intégral est difficile, mais je n'ai pas compris la méthode d'échantillonnage depuis longtemps (par exemple, je ne comprends pas PRML §11 ┐ (´ ー `) ┌ ). Cependant, récemment, j'ai parfois lu des articles utilisant des méthodes d'échantillonnage, j'ai donc décidé d'étudier à partir des bases.
Récemment secoué par un train dans le commerce de bétail de l'entreprise
Depuis que je lisais le livre, je voudrais résumer l'échantillonnage M-H et la méthode HMC qui apparaissent dans les chapitres 4 et 5. Le contenu est presque le même que celui de l'exemple du livre. Je voulais vraiment aller à l'annexe B pour l'échantillonnage de tranches et NUTS, mais mon travail a explosé et je n'ai pas eu assez de temps (j'en ferai plus plus tard).
Après avoir organisé le code suivant, je le téléchargerai sur github ou bitbucket.
exemple
La distribution de Poisson est utilisée comme distribution de probabilité d'événements rares, et la distribution gamma est utilisée comme distribution antérieure. La distribution gamma étant une distribution a priori conjuguée de la distribution de Poisson, l'échantillonnage n'est pas nécessaire en premier lieu, mais il est utilisé comme exemple (§3 de ce livre).
Illustration de la distribution de Poisson
sample.py
import numpy as np
import scipy.stats as sst
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
###Distribution de Poisson (moyenne 2.5)Exemple
from scipy.stats import poisson
mu = 2.5
x = np.arange(poisson.ppf(0.01, mu), poisson.ppf(0.99, mu))
plt.plot(x, poisson.pmf(x, mu), 'bo', ms=8, label='poisson pml')
plt.vlines(x, 0, poisson.pmf(x, mu), colors='b', lw=5, alpha=0.5)

Introduction de la distribution gamma comme distribution préalable et calcul de la distribution postérieure
La distribution postérieure est calculée en supposant que les données (0, 1, 0, 0, 2, 0, 1, 0, 0, 1) qui semblent être la distribution de Poisson sont correctement observées. Comme je l'ai écrit ci-dessus, puisqu'il s'agit en premier lieu d'une distribution antérieure conjuguée, la forme de la distribution postérieure peut être comprise.
sample.py
#Les données
x_data = np.array([0, 1, 0, 0, 2, 0, 1, 0, 0, 1])
#Distribution antérieure (distribution gamma avec une moyenne de 2))
f_prev = gamma(a=6.0, scale=1.0/3.0)
x = np.linspace(0.0, 5.0, 100)
plt.plot(x, f_prev.pdf(x), 'b-', label='Prev')
#Distribution ex post
n = x_data.shape[0]
ap = np.sum(x_data)
print("observe {0} positive {1}".format(n, ap))
f_post = gamma(a=6.0+ap, scale=1.0/(3.0 + n))
plt.plot(x, f_post.pdf(x), 'r--', label='Post')
plt.legend()

Échantillonnage par la méthode Metropolis-Hastings
Soit le paramètre $ \ theta $. Pour la valeur courante $ \ theta ^ {(t)} $ et la valeur $ \ theta_a $ échantillonnée à partir de la distribution proposée, il est probabiliste de déterminer si $ \ theta_a $ est requis.
Dans le cas de la distribution de Poisson et de la distribution gamma cette fois, la distribution postérieure que l'on veut trouver est proportionnelle au produit de la vraisemblance et de la distribution a priori (distribution gamma avec les paramètres α = 11, λ = 13 dans l'exemple) selon la loi de Bayes, donc $ r $ En transformant la formule de
sample.py
#Les données
x_data = np.array([0, 1, 0, 0, 2, 0, 1, 0, 0, 1])
#Responsabilité
def log_likelihood(x, theta):
x_probs = poisson.pmf(x, theta)
return np.sum(np.log(x_probs))
#Noyau de distribution gamma
def k_fg(theta, a, lbd): return np.exp(-lbd * theta) * (theta ** (a-1))
#Distribution proposée;Thêta moyen,Écart type 0.Distribution normale de 5
def q(x, theta): return sst.norm.pdf(x, loc=theta, scale=0.5)
# M-Boucle H (valeur initiale 1.0, 1000 fois)
def metropolis_raw(N):
current = 1.0 #valeur initiale
sample = []
sample.append(current)
for iter in range(N):
a = sst.norm.rvs(loc=prop_m, scale=prop_sd)
if a < 0: # reject (Dans la distribution proposée
sample.append(sample[-1])
continue
T_next = q(current, a) * k_fg(a, a=11.0, lbd=13.0) * log_likelihood(x_data, a)
T_prev = q(a, current) * k_fg(current, a=11.0, lbd=13.0) * log_likelihood(x_data, current)
ratio = T_next / T_prev
if ratio < 0: # reject
sample.append(sample[-1])
if ratio > 1 or ratio > sst.uniform.rvs():
sample.append(a)
current = a
else:
sample.append(sample[-1])
return np.array(sample)
N = 10000
theta = metropolis_raw(N)
n_burn_in = 1000
# theta trace
plt.figure(figsize=(10, 3))
plt.xlim(0, len(theta)-n_burn_in)
plt.title("Trace plot from M-H sampling. burn-in:{}".format(n_burn_in))
plt.plot(theta[n_burn_in:], alpha=0.9, lw=.3)
# plot samples
plt.figure(figsize=(5,5))
plt.title("Histgram from M-H sampling.")
plt.hist(theta[n_burn_in:], bins=50, normed=True, histtype='stepfilled', alpha=0.2)
xx = np.linspace(0, 2.5,501)
plt.plot(xx, sst.gamma(11.0, 0.0, 1/13.).pdf(xx))
plt.show()
La mise en œuvre est fausse, ce n'est pas si bon


Méthode M-H indépendante
Dans l'exemple ci-dessus, la distribution normale (paramètres donnés) a été utilisée comme distribution proposée, mais n'est-ce pas correct si f et q sont indépendants en premier lieu? → Méthode M-H indépendante
sample.py
import scipy.stats as sst
#Distribution proposée;distribution normale(Paramètres fixes)
prop_m, prop_sd = 1.0, 0.5
def q(x): return sst.norm.pdf(x, loc=prop_m, scale=prop_sd)
#Remplacez le calcul de a et r
a = sst.norm.rvs(loc=prop_m, scale=prop_sd)
r = (q(current)*k_fg(a,a=11.0, lbd=13.0)) / (q(a)*k_fg(current,a=11.0,lbd=13.0))


Je m'inquiète pour la mise en œuvre.
Méthode M-H de marche aléatoire
Marchons au hasard les points candidats (balle droite) → Si une distribution normale est utilisée, la valeur proposée (a) et la variance jusqu'à présent sont correctement incluses dans la moyenne.
sample.py
current = 4.0
list_theta = []
list_theta.append(current)
#Pour une marche aléatoire (flouter les paramètres donnés en moyenne)
def f_g(theta):
prop_sd = np.sqrt(0.1)
return sst.norm.rvs(loc=theta, scale=prop_sd)
###Remplacer la partie calculée de a et r
a = f_g(current)
r = f_gamma(a) / f_gamma(current)


Ce sera un peu mieux si vous augmentez le nombre de répétitions.
Bonus (fonction scipy)
La capacité d'échantillonnage de la famille principale.
sample.py
import scipy.stats as sst
lbd = 1.0/13
plt.rcParams["figure.figsize"] = [4, 4]
a = 11.0
rv = sst.gamma(a, scale=lbd)
x = np.linspace(sst.gamma.ppf(0.01, a, scale=lbd), sst.gamma.ppf(0.99, a, scale=lbd), 100)
plt.plot(x, rv.pdf(x), 'r-', lw=5, alpha=0.6, label='gamma pdf')
plt.plot(x, rv.pdf(x), 'k-', lw=2, label='frozen pdf')
vals = rv.ppf([0.001, 0.5, 0.999])
np.allclose([0.001, 0.5, 0.999], sst.gamma.cdf(vals, a, scale=lbd))
r = sst.gamma.rvs(a, scale=lbd,size=9000)
plt.hist(r, normed=True, bins=100, histtype='stepfilled', alpha=0.2)
plt.legend(loc='best', frameon=False)

Méthode HMC
J'ai appris en physique au lycée que l'énergie mécanique (énergie cinétique + énergie de position) est préservée lorsqu'aucune force externe n'est appliquée (aucune autre perte due à la lumière ou à la chaleur). Il devrait y avoir beaucoup de monde. En mécanique analytique, ceci est lu comme hamiltonien et discuté en coordonnées généralisées. Comme il est mis de côté (probablement écrit plus tôt lorsque vous ouvrez un livre de mécanique analytique approprié)
Je vais laisser les détails au livre, mettre la distribution postérieure logarithmique comme $ -h (\ theta) $, calculer l'hamiltonien comme $ h (x) + \ frac {1} {2} p ^ 2 $, et suivre les étapes La méthode HMC est la méthode d'échantillonnage avec (dans le cas d'une dimension).
- [Méthode Leap Frog](https://ja.wikipedia.org/wiki/%E3%83%AA%E3%83%BC%E3%83%97%E3%83%BB%E3%83%95 % E3% 83% AD% E3% 83% 83% E3% 82% B0% E6% B3% 95) Déterminez $ \ epsilon, L, T $ comme paramètres de.
- Déterminez la valeur initiale $ \ theta ^ {(0)} $ et définissez $ i = 0 $ (répétez 3 à 6 jusqu'à ce que le $ i $ spécifié)
- Échantillon de la distribution normale standard… $ p ^ {(i)} \ sim \ mathcal {N} (p ^ {(i)} \ mid 0, 1) $
- Modifiez les étapes $ \ theta ^ {(i)} $ et $ p ^ {(i)} $ par L par la méthode saut de grenouille, et changez les points candidats $ \ theta ^ {(a)}, p ^ {(a) } $
- $ r = \ exp \ (H (\ theta ^ {(t)}, p ^ {(t)}) --H (\ theta ^ {(a)}, p ^ {(a)}) ) En tant que $, acceptez 5 magasins auxiliaires avec une probabilité de $ \ min (1, r) $, et jetez-les autrement.
- t = t+1
Implémentons-le et voyons comment cela fonctionne. Modèle de distribution de Poisson-distribution Gamma avec distribution postérieure excluant les constantes de normalisation
hmc_sample.py
#Définition de la différenciation de h et h
alpha, lbd = 11, 13
def _h(theta, alpha, lbd):
return lbd * theta - (alpha - 1) * np.ma.log(theta)
def _hp(theta, alpha, lbd):
return lbd - (alpha - 1) / theta
h = lambda theta: _h(theta, alpha, lbd)
hp = lambda theta: _hp(theta, alpha, lbd)
###Hamiltonien
def H(theta, p):
return h(theta) + 0.5 * p * p
###Implémentation simple de la méthode de saut de grenouille
def lf(_th, _p, epsilon, L):
l_p = [_p]
l_th = [_th]
for tau in range(1, L):
p_t = l_p[-1]
theta_t = l_th[-1]
# 1/2
p_t_half = p_t - 0.5 * epsilon * hp(theta_t)
# update
next_theta = theta_t + epsilon * p_t_half
next_p = p_t_half - 0.5 * epsilon * hp(next_theta)
# store
l_p.append(next_p)
l_th.append(next_theta)
return (l_th[-1], l_p[-1])
###Échantillonnage HMC
N = 10000
moves = []
theta = [2.5]
p = []
L = 100
epsilon = 0.01
for itr in range(N):
pv = sst.norm.rvs(loc=0, scale=1, size=1)[0]
p.append(pv)
# candidate by LF
curr_th, curr_p = theta[itr], p[itr]
cand_th, cand_p = lf(curr_th, curr_p, epsilon, L)
# compute r by exp(H(curr) - H(cand))
Hcurr = H(curr_th, curr_p)
Hcand = H(cand_th, cand_p)
r = np.exp(Hcurr - Hcand)
# print("{0}\t{1:2.4f}\t{2:2.4f}".format(itr, cand_th, cand_p))
# print("\t\t\t{0:2.3f}\t{1:2.3f}\t{2:2.3f}".format(Hcurr, Hcand, r))
if r < 0:
#reject
theta.append(theta[-1])
p.append(p[-1])
continue
if r >= 1 or r > sst.uniform.rvs():
theta.append(cand_th)
p.append(cand_p)
moves.append( (curr_th, cand_th, curr_p, cand_p) )
curr_th, curr_p = cand_th, cand_p
else:
#Reject
theta.append(theta[-1])
Tracés de trace et d'histogramme.


Bonnes vibrations.
Dessiner des lignes de contour
hmc_sample.py
lin_p = np.linspace(-6.5, 6.5, 100.0)
lin_theta = np.linspace(0.01, 3.51, 100.0)
X, Y = np.meshgrid(lin_theta, lin_p)
Z = H(X, Y)
# 1dim h(theta)
xx = np.linspace(0.01, 3.01, 100)
plt.figure(figsize=(14, 7))
plt.title("h")
plt.plot(xx, h(xx), lw='1.5', alpha=0.8, color='r')
plt.xlim(-0.1, 3.5)
plt.xlabel("theta")
plt.ylabel("h(theta)")
# 2dim
plt.figure(figsize=(14,7))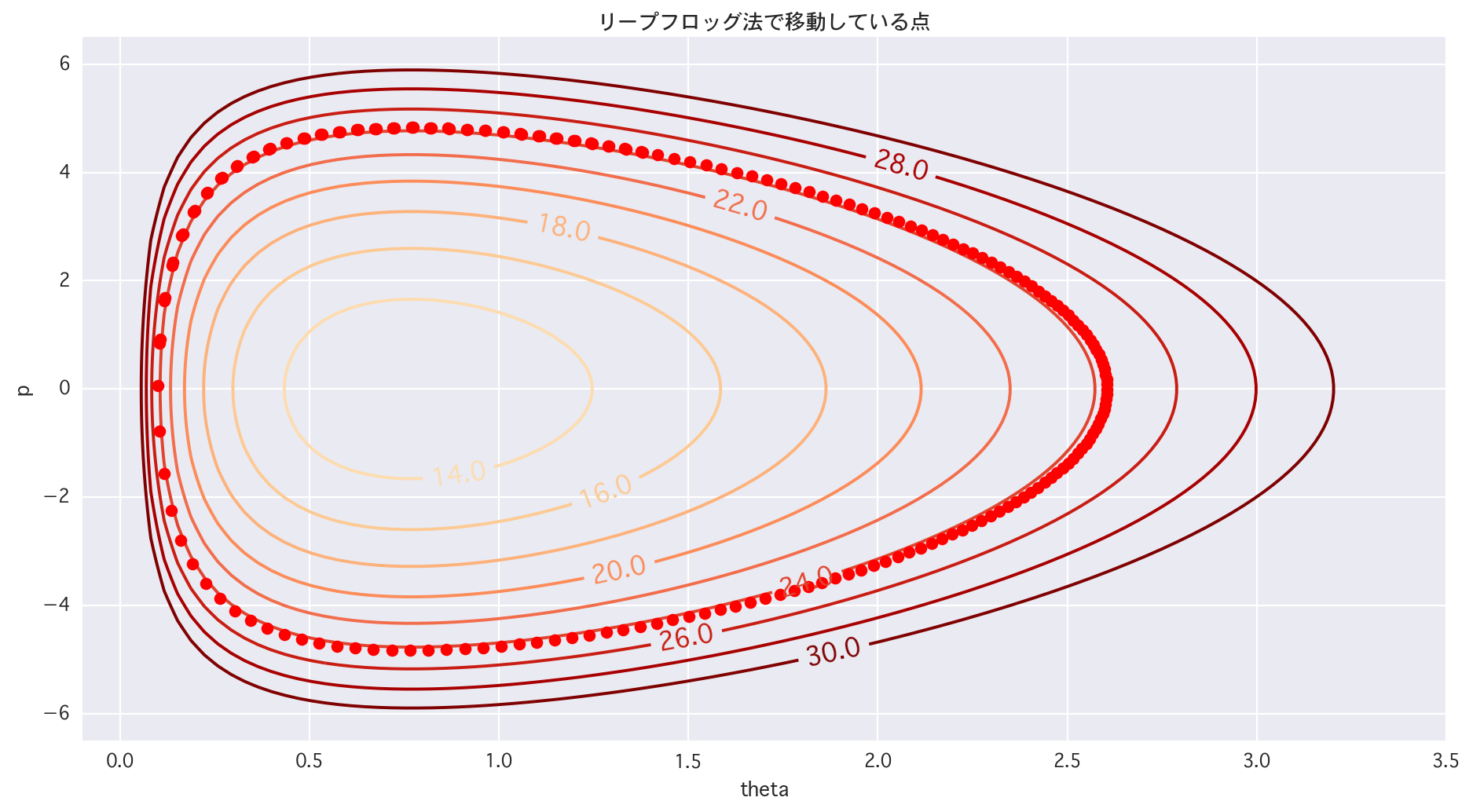
cont = plt.contour(X, Y, Z, levels=[i for i in range(10, 32, 2)], cmap="OrRd")
cont.clabel(fmt='%2.1f', fontsize=14)
plt.xlim(-0.1, 3.5); plt.ylim(-6.5, 6.5); plt.xlabel("theta"); plt.ylabel("p"); plt.show()


hmc_smaple.py
# 2dim (trace of LF)
# 1/4 zones
plt.figure(figsize=(14,7))
cont = plt.contour(X, Y, Z, levels=[i for i in range(10, 32, 2)], cmap="OrRd")
cont.clabel(fmt='%2.1f', fontsize=14)
for tau in range(1, len(p)):
plt.plot(theta[tau], p[tau], 'ro')
plt.title(u"Le point de se déplacer par la méthode de saut de grenouille")
plt.xlim(-0.1, 3.5)
plt.ylim(-6.5, 6.5)
plt.xlabel("theta")
plt.ylabel("p")
plt.show()
Je ressens le désir de sauver l'hamiltonien (approprié)

hmc_sample.py
#De quel point à quel point
# 1/4 zones
plt.figure(figsize=(14,7))
cont = plt.contour(X, Y, Z, levels=[i for i in range(10, 32, 2)], cmap="OrRd")
cont.clabel(fmt='%2.1f', fontsize=14)
# for tau in range(1, len(p)):
# plt.plot(theta[tau], p[tau], 'ro')
plt.title(u"Le point de se déplacer par la méthode de saut de grenouille")
plt.xlim(-0.1, 3.5)
plt.ylim(-6.5, 6.5)
plt.xlabel("theta")
plt.ylabel("p")
for i in range(len(moves)):
t0, t1, p0, p1 = moves[i][0], moves[i][1], moves[i][2], moves[i][3]
# plt.plot([t0, t1], [p0, p1], 'r-')
plt.plot([t0, t1], [p0, p1], 'r-')
plt.plot(t0, p0, 'ro')
plt.plot(t1, p1, 'bo')
plt.show()

Il y a de l'apprentissage lorsque vous le déplacez réellement.
des plans
Ce que j'ai laissé sera digéré et mis à jour plus tard cette année (drapeau)
- Slice Sampling
- NUTS
Recommended Posts