[Introduction] J'ai essayé de l'implémenter moi-même tout en expliquant pour comprendre la dichotomie

Pour comprendre la dichotomie

Qu'est-ce qu'un arbre bifurqué?

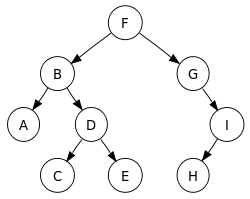
C'est une sorte de structure de données non linéaire ayant une structure arborescente.

Tree ADT ne considère pas l'ordre des éléments.

Chaque nœud a de 0 à 2 enfants. Par conséquent, la racine et le sous-arbre gauche qui se développe à gauche de la racine et le sous-arbre droit qui se développe vers la droite peuvent être généralement visualisés.

[Explication des dichotomies par Wikipedia](https://ja.wikipedia.org/wiki/%E6%9C%A8%E6%A7%8B%E9%80%A0_(%E3%83%87%E3%) 83% BC% E3% 82% BF% E6% A7% 8B% E9% 80% A0))

Objectif

• Je souhaite approfondir ma compréhension des structures de données et des algorithmes en apprenant la dichotomie.
• Implémentez la structure de données de dichotomie en python.
• Comprendre comment gérer les structures de données de dichotomie, pas seulement la mise en œuvre de la dichotomie.
• Creuser en profondeur l'arbre de dichotomie de base pour approfondir la compréhension de l'arbre de dichotomie ⇒ Article parent

Contenu

Structure des données et définition des nœuds

• Le nœud a une valeur (node.data)
• Avoir une connexion à un nœud enfant (node.left = Node (data))
• Le nombre d'enfants est de 0, 1 ou 2.
• Le nœud supérieur est le nœud racine (self.root, ins.root)

Implémentation d'arbre bifurqué

Générer un objet Node ()

Créez un objet Node et générez les éléments suivants dans le constructeur. .Left et .right sont également None car ils n'ont rien à voir avec les autres au moment de la génération.

• Valeur du nœud: self.data = data
• Lien vers le nœud enfant du sous-arbre gauche: self.left = None
• Lien vers le nœud enfant du sous-arbre droit: self.right = None

Node_class.py

class Node:
    """ Node is user data structure　as binary tree  """
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

Génération d'arbres de bisection

1. Créez un objet Node
2. Trouvez la partie où l'enfant n'a pas d'élément et insérez le nœud.
3. Il existe plusieurs méthodes qui traversent le nœud, en tenant compte de l'ordre des visites.

Points au moment de la mise en œuvre

• Créez un nœud racine dans le constructeur.
• Introduisez une fonction pour insérer une valeur dans le constructeur.
• L'implémentation ci-dessus est définie après être apparue comme une méthode d'instance
• Si vous souhaitez quitter la méthode depuis l'intérieur du while dans la méthode, terminez-la par return

binary_tree.py

class BinaryTree:
    """ user difine data structure BinaryTree """
    def __init__(self, arr):
        self.root = None #Créez une racine vide pour servir de base à un traitement futur

        for inserted_node_data in arr: #Traitement pour insérer séquentiellement les valeurs des nœuds stockés dans la liste
            print('....')
            print('try inserting ', inserted_node_data)
            self.insert(inserted_node_data)

    def insert(self, data):     #Processus d'insertion (génération de route ⇒ générer la branche de chaque nœud) ・ ・ ・ La valeur de la branche gauche est inférieure à celle du nœud actuel
        if self.root == None:   #Parce que le nœud racine est un nœud spécial qui sert de base à l'analyse de l'arborescence.Cas à générer séparément en tant que root
            print('Root node is ....')
            self.root = Node(data) # Node()Créer et attribuer une instance
            print(self.root.data)

        else:
            level = 1
            flag = True
            next_queue = [self.root] #Créer la première file d'attente
            while flag:   #flag devient False lorsque tous les éléments sont None
                temp_queue, next_queue = next_queue, []
                level += 1

                for node in temp_queue:
                    #Branche gauche
                    #Ajouter le nœud chiled du nœud actuel à la file d'attente de l'opération suivante
                    if node.left is not None:
                        next_queue.append(node.left)
                    #Lorsqu'aucun n'est trouvé dans le nœud enfant, créez un nouveau nœud à l'aide des données
                    else:
                        node.left = Node(data)
                        print('In level {}, {} is inseted'.format(level, data))
                        """
                        （AA）
Après avoir ajouté des données au nœud, cette insertion se termine
Voici pour< while <Puisqu'il s'agit de la méthode insert, utilisez return pour terminer la méthode en un seul coup
                        """
                        return 

                    #Branche droite
                    #Ajouter le nœud chiled du nœud actuel à la file d'attente de l'opération suivante
                    if node.right is not None:
                        next_queue.append(node.right)
                    #Lorsqu'aucun n'est trouvé dans le nœud enfant, créez un nouveau nœud à l'aide des données
                    else:
                        node.right = Node(data)
                        print('In level {}, {} is inseted'.format(level, data))
                        """
Voir (AA)
                        """
                        return

                flag = any(next_queue)

    ##########################
    #  Tree traversal
    ##########################
    def preoder_traversal(self, node, res):
        if node != None:
            print('queue', node.data)
            res.append(node.data)

            #Sous-arbre gauche dans l'ordre précédent
            self.preoder_traversal(node.left, res)
            #Sous-arbre droit dans l'ordre précédent
            self.preoder_traversal(node.right, res)

        return res

    def inoder_traversal(self, node, res):
        if node != None:

            #Sous-arbre gauche dans l'ordre
            self.inoder_traversal(node.left, res)

            print('queue', node.data)
            res.append(node.data)

            #Sous-arbre droit dans l'ordre
            self.inoder_traversal(node.right, res)
        return res

    def postorder_traversal(self, node, res):
        if node != None:
            self.postorder_traversal(node.left, res)
            self.postorder_traversal(node.right, res)
            print('queue', node.data)
            res.append(node.data)
        return res

    def level_order_traversal(self, queue, res= []):

        if queue == [] :
            # it's root
            print('root', self.root.data)
            res.append(self.root.data)
            queue.append(self.root)

        else:
            #Le nœud de ce niveau étant une file d’arguments, tournez-le avec pour
            temp_list, queue = queue, []
            not_none_cnt = 0

            for item in temp_list:
                if item.left is not None:
                    res.append(item.left.data)
                    print('queue', item.left.data)
                    queue.append(item.left)
                    not_none_cnt += 1

                if item.right is not None:
                    res.append(item.right.data)
                    print('queue', item.right.data)
                    queue.append(item.right)
                    not_none_cnt += 1

            if not_none_cnt == 0:
                return #Revenez à l'endroit où vous avez appelé cette fonction pour la dernière fois

        self.level_order_traversal(queue, res)

        return res

Méthode bifurquée

Implémentation de méthodes pour rechercher la valeur maximale, rechercher la présence ou l'absence d'une valeur, vérifier la taille et vérifier la hauteur. Voir les commentaires dans le code pour les points.

bt_method.py

#Méthode bifurquée
class BT_method(BinaryTree):
    def __init__(self, arr):
        super().__init__(arr)

    def max_in_binary_tree(self, node, temp_max):
        """La mise en œuvre montre la valeur maximale dans la relation parent-enfant
Il en va de même même si vous LIFO en parcourant et en laissant une grande valeur.
Identique à la mémorisation de la valeur maximale lors de la navigation en recherche avant"""
        if node is not None:
            temp_root_val = node.data
            left_val = self.max_in_binary_tree(node.left, temp_max)
            right_val = self.max_in_binary_tree(node.right, temp_max)

            temp_max = max(temp_root_val, left_val, right_val, temp_max)

        return temp_max

    def find_val(self, node, val, flag=False):
        if node != None:
            if node.data == val:
                return True

            else:
                flag_left = self.find_val(node.left, val) #Puisque le résultat de la récurrence est renvoyé par retour, il est reçu sous forme de variable
                flag_right = self.find_val(node.right, val)

                if flag_left or flag_right:
                    return True

        return False


    def size(self, node):
        if node is None: #Fin du comptage lorsque le nœud est Aucun
            return 0 #Si 0 est renvoyé, il ne sera pas compté
        else:
            left_cnt = self.size(node.left)
            right_cnt = self.size(node.right)

            return 1 + left_cnt + right_cnt #I (not None) vaut 1 et le nombre dans les arbres gauche et droit (la recherche virtuelle est réalisée par une fonction récursive)


    def hight(self, level=0):
        flag = True
        queue = [self.root]

        while flag:
            level += 1
            temp_list, queue = queue, []
            for node in temp_list:
                if node.left is not None:
                    queue.append(node.left)
                if node.right is not None:
                    queue.append(node.right)


            flag = any(queue)

        return level

Courir

J'ai exécuté le code comme ci-dessous.

main.py

ins = BinaryTree(range(1,16))

print('--------------------------')
print('start preoder traversal')
print(ins.preoder_traversal(ins.root, []))

print('--------------------------')
print('start inoder traversal')
print(ins.inoder_traversal(ins.root, []))

print('--------------------------')
print('start postoder traversal')
print(ins.postorder_traversal(ins.root, []))

print('--------------------------')
print('start level order traversal')
print(ins.level_order_traversal([]))

#
print('=====================================')

ins2 = BT_method(range(1,16))
print('--------------------------')
print('find max')
print(ins2.max_in_binary_tree(ins2.root, 0))
print('--------------------------')
print('find value')
print('looking for 7', ins2.find_val(ins2.root, 7))
print('looking for 17', ins2.find_val(ins2.root, 17))


#  search size
print('--------------------------')
print('detect node size')
print(ins2.size(ins2.root))

Résultat d'exécution

La partie d'impression nous indique le comportement séquentiellement

....
try inserting  1
Root node is ....
1
....
try inserting  2
In level 2, 2 is inseted
....
try inserting  3
In level 2, 3 is inseted
....
try inserting  4
In level 3, 4 is inseted
....
try inserting  5
In level 3, 5 is inseted
....
try inserting  6
In level 3, 6 is inseted
....
try inserting  7
In level 3, 7 is inseted
....
try inserting  8
In level 4, 8 is inseted
....
try inserting  9
In level 4, 9 is inseted
....
try inserting  10
In level 4, 10 is inseted
....
try inserting  11
In level 4, 11 is inseted
....
try inserting  12
In level 4, 12 is inseted
....
try inserting  13
In level 4, 13 is inseted
....
try inserting  14
In level 4, 14 is inseted
....
try inserting  15
In level 4, 15 is inseted
--------------------------
start preoder traversal
queue 1
queue 2
queue 4
queue 8
queue 9
queue 5
queue 10
queue 11
queue 3
queue 6
queue 12
queue 13
queue 7
queue 14
queue 15
[1, 2, 4, 8, 9, 5, 10, 11, 3, 6, 12, 13, 7, 14, 15]
--------------------------
start inoder traversal
queue 8
queue 4
queue 9
queue 2
queue 10
queue 5
queue 11
queue 1
queue 12
queue 6
queue 13
queue 3
queue 14
queue 7
queue 15
[8, 4, 9, 2, 10, 5, 11, 1, 12, 6, 13, 3, 14, 7, 15]
--------------------------
start postoder traversal
queue 8
queue 9
queue 4
queue 10
queue 11
queue 5
queue 2
queue 12
queue 13
queue 6
queue 14
queue 15
queue 7
queue 3
queue 1
[8, 9, 4, 10, 11, 5, 2, 12, 13, 6, 14, 15, 7, 3, 1]
--------------------------
start level order traversal
root 1
queue 2
queue 3
queue 4
queue 5
queue 6
queue 7
queue 8
queue 9
queue 10
queue 11
queue 12
queue 13
queue 14
queue 15
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
=====================================
....
try inserting  1
Root node is ....
1
....
try inserting  2
In level 2, 2 is inseted
....
try inserting  3
In level 2, 3 is inseted
....
try inserting  4
In level 3, 4 is inseted
....
try inserting  5
In level 3, 5 is inseted
....
try inserting  6
In level 3, 6 is inseted
....
try inserting  7
In level 3, 7 is inseted
....
try inserting  8
In level 4, 8 is inseted
....
try inserting  9
In level 4, 9 is inseted
....
try inserting  10
In level 4, 10 is inseted
....
try inserting  11
In level 4, 11 is inseted
....
try inserting  12
In level 4, 12 is inseted
....
try inserting  13
In level 4, 13 is inseted
....
try inserting  14
In level 4, 14 is inseted
....
try inserting  15
In level 4, 15 is inseted
--------------------------
find max
15
--------------------------
find value
looking for 7 True
looking for 17 False
--------------------------
detect node size
15

Les références

• Introduction à la structure des données et à l'algorithme (O'Reilly)
• [Explication de la bifurcation par Wikipedia](https://ja.wikipedia.org/wiki/%E6%9C%A8%E6%A7%8B%E9%80%A0_(%E3%83%87%E3) % 83% BC% E3% 82% BF% E6% A7% 8B% E9% 80% A0))