DBSCAN (clustering) avec scikit-learn
À propos de la présentation de DBSCAN, l'un des algorithmes de clustering et de réglage simple des paramètres Je ne semblais pas avoir d'article japonais complet, alors je l'ai écrit. Veuillez noter que le plan de DBSCAN est une traduction japonaise (approximative) de wikipedia.
Qu'est-ce que DBSCAN
- Abréviation de «Clustering spatial basé sur la densité des applications avec bruit»
- L'un des algorithmes de clustering
Aperçu de l'algorithme
-
- Classez les points en 3 catégories
- Point central: un point avec au moins minPts de points adjacents dans un rayon de ε
- Points joignables (points frontières): points qui n'ont pas autant de points adjacents que minPts dans le rayon ε, mais qui ont des points centraux dans le rayon ε
- Valeur aberrante: points sans points adjacents dans le rayon ε
-
- Créez un cluster à partir d'une collection de points Core et attribuez des points accessibles à chaque cluster.
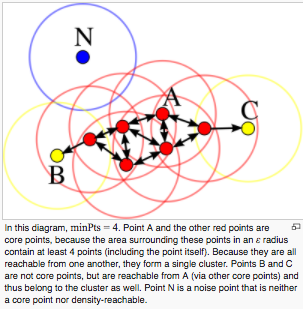
- Créez un cluster à partir d'une collection de points Core et attribuez des points accessibles à chaque cluster.
[D'après la figure wikipedia]
Avantages
- Contrairement à k-means, vous n'avez pas à décider d'abord du nombre de clusters
- Peut être classé même en grappes pointues. Ne suppose pas que le cluster est sphérique
- Robuste pour les valeurs aberrantes.
- Il peut y avoir deux paramètres, ε et minPts. Il est également facile de déterminer la plage de paramètres.
Désavantages
- Le concept de points de frontière est subtil et peut changer le cluster auquel il appartient en fonction des données.
- La précision varie en fonction de la méthode de calcul de la distance.
- Il est difficile de déterminer correctement ε et minPts lorsque les données sont denses. Dans certains cas, la plupart des points sont classés en un seul cluster.
- Il est difficile de déterminer ε sans connaître les données.
- (Non limité à DBSCAN) Au fur et à mesure que la dimension grandit, elle est affectée par la malédiction de la dimension.
Différence par rapport aux autres algorithmes
Il s'agit d'une comparaison de chaque méthode dans la page de démonstration scikit-learn, mais la seconde en partant de la droite est DBSCAN. Vous pouvez voir intuitivement qu'ils sont regroupés en fonction de la densité.
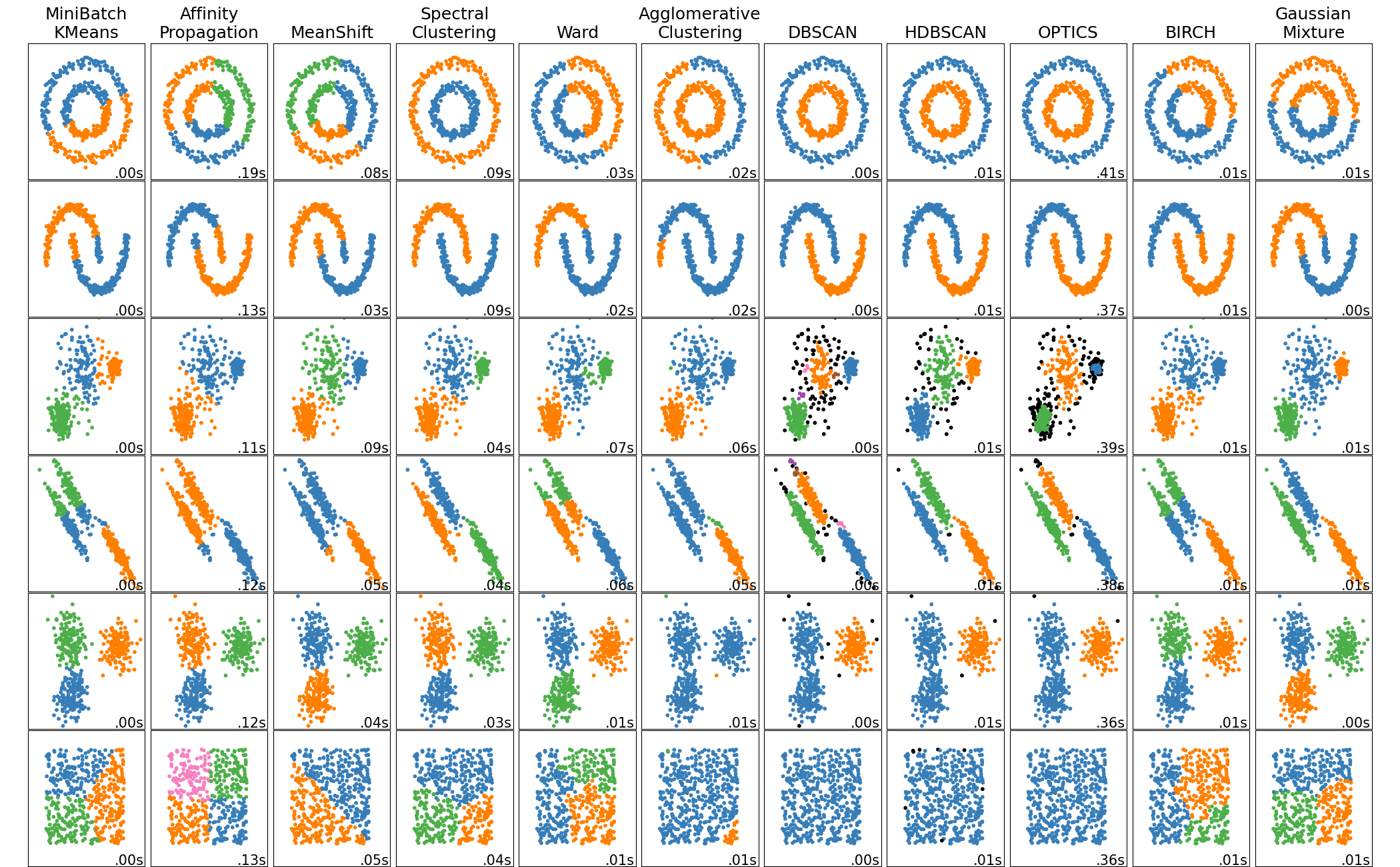
Réglage de ε et minPts
S'il est bidimensionnel, il peut être visualisé pour déterminer s'il est bien classé, mais s'il est tridimensionnel ou plus, il est difficile à visualiser et à juger. J'ai débogué et ajusté la prise et le nombre de clusters comme suit. (Utilisation de scikit-learn)
from sklearn.cluster import DBSCAN
for eps in range(0.1,3,0.1):
for minPts in range(1,20):
dbscan = DBSCAN(eps=eps,min_samples=minPts).fit(X)
y_dbscan = dbscan.labels_
print("eps:",eps,",minPts:", minPts)
#nombre de valeurs aberrantes
print(len(np.where(y_dbscan ==-1)[0]))
#Nombre de clusters
print(np.max(y_dbscan)))
#Nombre de points dans le cluster 1
print(len(np.where(y_dbscan ==0)[0]))
#Nombre de points dans le cluster 2
print(len(np.where(y_dbscan ==1)[0]))
Liens reliés à DBSCAN
- wikipedia
- https://en.wikipedia.org/wiki/DBSCAN
- Documentation officielle
- http://scikit-learn.org/stable/modules/generated/sklearn.cluster.DBSCAN.html
- Page de démonstration officielle
- http://scikit-learn.org/stable/auto_examples/cluster/plot_dbscan.html
- Qiita
- http://qiita.com/ynakayama/items/46d5f2e49f57c7de98a4
- http://qiita.com/yamaguchiyuto/items/82c57c5d44833f5a33c7
Postscript
La version japonaise de Wikipedia a été mise à jour avec des descriptions supplémentaires. C'est facile à comprendre.
Recommended Posts