Expliquez ce qu'est la méthode de descente de gradient stochastique en l'exécutant en Python
À quoi sert la méthode de descente de gradient?
La méthode de descente de gradient est souvent utilisée dans les statistiques et l'apprentissage automatique. En particulier, l'apprentissage automatique aboutit souvent à la résolution numérique d'un problème qui minimise (maximise) certaines fonctions. (Par exemple, méthode du carré minimum → Minimiser la somme des carrés des erreurs (Référence), Déterminer les paramètres du réseau neuronal, etc ...)
Donc, fondamentalement, c'est un problème de trouver un endroit où il se différencie et devient 0, différencié en 0. Donc, c'est cette méthode de descente de gradient qui est importante lors de la résolution par programme de la valeur qui est différenciée à 0. Il existe plusieurs types de méthodes de gradient, mais nous traiterons ici de la méthode de descente la plus raide et de la méthode de descente de gradient stochastique. Tout d'abord, je voudrais vérifier avec un graphique unidimensionnel pour obtenir une image.
Pour une dimension
Dans le cas d'une dimension, il n'y a pas de concept de probabilité, c'est juste une méthode de descente de gradient. (Que voulez-vous dire plus tard) Pour l'exemple unidimensionnel, utilisons celui avec la distribution normale moins. Les graphiques de $ x_ {init} = 0 $ et $ x_ {init} = 6 $ sont utilisés comme exemples. Le graphique cible était celui dans lequel la fonction de densité de la distribution normale était soustraite et tournée vers le bas.
** Graphique avec valeur initiale = 0 **
Vous pouvez voir qu'il commence à la fin du graphique et converge à la valeur minimale au plus petit point. Le graphique linéaire bleu est la version négative de la distribution normale et le graphique linéaire vert est le graphique des valeurs différenciées.
** Graphique avec valeur initiale = 6 **

Déterminez la valeur $ x $ suivante en fonction de la pente à chaque point, vérifiez la pente à cette position, puis descendez, et ainsi de suite pour atteindre la valeur minimale (en fait la valeur minimale). Dans l'exemple ci-dessus, la pente devient douce à mesure qu'elle s'approche de la valeur minimale, de sorte que la quantité de progression dans une étape diminue progressivement et lorsqu'elle devient plus petite qu'une certaine norme, elle s'arrête. Je vais.
Le code qui a écrit ces deux graphiques est ici.
2D (fonction quadratique)
Dans le cas de multi-dimensionnel, il descendra en considérant la direction pour passer à l'étape suivante. Les caractéristiques du mouvement changent en fonction de la fonction cible, mais j'ai d'abord dessiné un graphique en utilisant la fonction quadratique $ Z = -3x ^ 2-5y ^ 2 + 6xy $ comme exemple. Vous pouvez le voir se déplacer vers le haut tout en se déplaçant en zigzag.
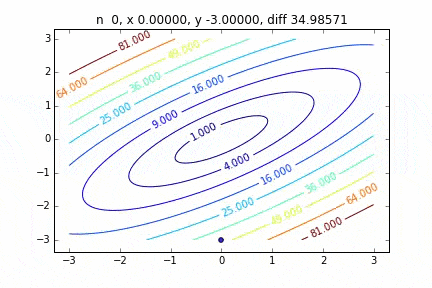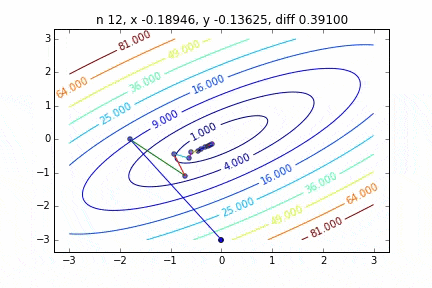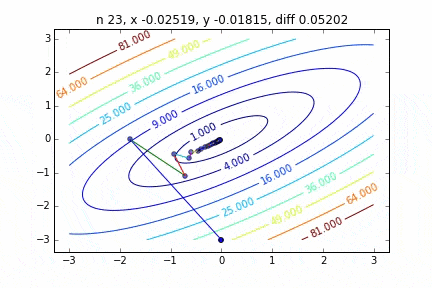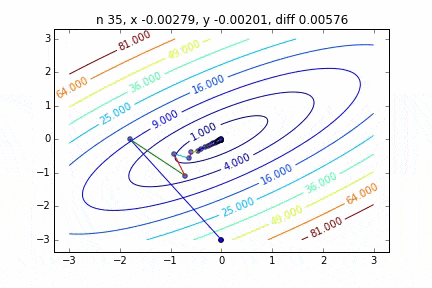
Le code est ici
Pour 2D
Dans le cas de la 2D (distribution normale 2D)
On a constaté que lorsque la méthode de descente la plus raide est appliquée à une distribution normale bidimensionnelle (moins), elle ne se déplace pas en zigzag et descend proprement à la valeur minimale. Je voudrais étudier la différence d'état de convergence en fonction de la fonction cible.

Le code est ici
Comment fonctionne la méthode de descente la plus raide
Le mécanisme de la méthode de descente la plus raide consiste à sélectionner d'abord le point de départ, puis le vecteur avec la plus grande pente de descente à ce point, c'est-à-dire
\nabla f = \frac{d f({\bf x})}{d {\bf x}} = \left[ \begin{array}{r} \frac{\partial f}{\partial x_1} \\ ... \\ \frac{\partial f}{\partial x_2} \end{array} \right]
Est le moyen de passer à l'étape suivante en utilisant. Dans le graphique ci-dessus, ce vecteur de gradient multiplié par le taux d'apprentissage $ \ eta $ est représenté par une ligne droite. Alors
x_{i+1} = x_i - \eta \nabla f
Le processus de répétition de cette étape jusqu'à ce qu'elle converge est exécuté.
Quelle est la méthode de descente de gradient probabiliste?
Maintenant, je voudrais passer à la méthode de descente de gradient stochastique. Tout d'abord, concernant la fonction cible, je voudrais expliquer l'utilisation de la fonction d'erreur de la droite de régression utilisée dans Explication of regression analysis. Il y a une partie qui change un peu l'interprétation (en utilisant la méthode la plus probable), donc [fin de phrase](http://qiita.com/kenmatsu4/items/d282054ddedbd68fecb0#http://qiita.com/kenmatsu4/items/d282054ddedbd68fecb0# Supplément Les paramètres de la droite de régression sont calculés par la méthode la plus probable) en supplément.
Les données sont,
y_n = \alpha x_n + \beta + \epsilon_n (\alpha=1, \beta=0)\\
\epsilon_n ∼ N(0, 2)
Prenons l'exemple de la préparation de N = 1000 ensembles de données et de la recherche de la droite de régression. Le diagramme de dispersion est le suivant.

Fonction d'erreur,
E({\bf w})=\sum_{n=1}^{N} E_n({\bf w}) = \sum_{n=1}^{N} (y_n -\alpha x_n - \beta)^2 \\
{\bf w} = (\alpha, \beta)^{\rm T}
Nous trouverons la valeur minimale de, mais d'abord, pour calculer le gradient, nous dérivons le vecteur de gradient qui est partiellement différencié par $ \ alpha et \ beta $, respectivement.
\frac{\partial E({\bf w})}{\partial \alpha} = \sum_{n=1}^{N} \frac{\partial E_n({\bf w})}{\partial \alpha} =
\sum_{n=1}^N (2 x_n^2 \alpha + 2 x_n \beta - 2 x_n y_n )\\
\frac{\partial E({\bf w})}{\partial \beta} = \sum_{n=1}^{N}\frac{\partial E_n({\bf w})}{\partial \alpha} =
\sum_{n=1}^N (2\beta + 2 x_n \alpha - 2y_n)
Le vecteur de gradient est donc
\nabla E({\bf w}) = \frac{d E({\bf w}) }{d {\bf w}} = \left[ \begin{array}{r} \frac{\partial E({\bf w})}{\partial \alpha} \\ \frac{\partial E({\bf w})}{\partial \beta} \end{array} \right] = \sum_{n=1}^{N}
\nabla E_n({\bf w}) = \sum_{n=1}^{N} \left[ \begin{array}{r} \frac{\partial E_n({\bf w})}{\partial \alpha} \\ \frac{\partial E_n({\bf w})}{\partial \beta} \end{array} \right]=
\left[ \begin{array}{r}
2 x_n^2 \alpha + 2 x_n \beta - 2 x_n y_n \\
2\beta + 2 x_n \alpha - 2y_n
\end{array} \right]
Ce sera.
Comme il est difficile de trouver une droite de régression simple, elle peut être résolue sous forme d'équation, mais nous allons le résoudre en utilisant la méthode de descente de gradient stochastique. Au lieu d'utiliser toutes les données de N = 1000 ici, la clé de cette méthode est de calculer le gradient pour les données extraites par échantillonnage aléatoire à partir d'ici et de décider de l'étape suivante.
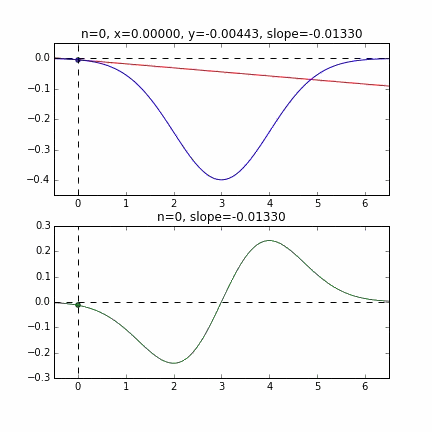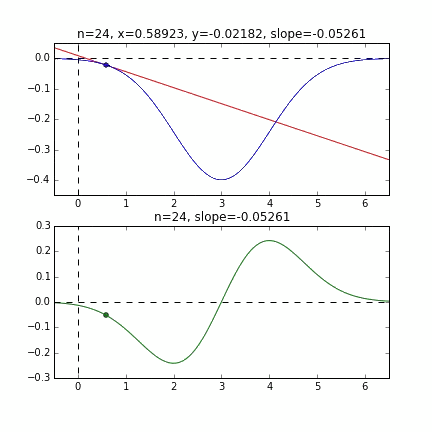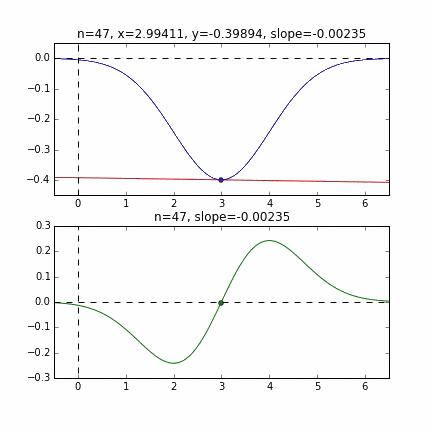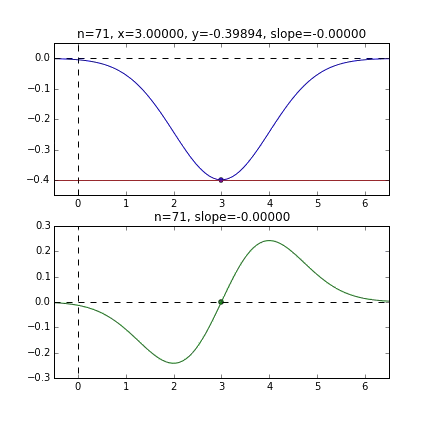
Tout d'abord, prenons 20 au hasard dans cet ensemble de données et créons un graphique. L'axe horizontal est $ \ alpha $, l'axe vertical est $ \ beta $ et l'axe Z est l'erreur $ E (\ alpha, \ beta) $.

Je pense qu'en quelque sorte les valeurs minimales du graphique sont dispersées autour de $ \ alpha = 1, \ beta = 0 $. Cette fois, j'ai choisi au hasard 3 données parmi 1000 données et j'ai écrit ce graphique en me basant sur celles-ci. La valeur initiale est $ \ alpha = -1,5, \ beta = -1,5 $, le taux d'apprentissage est proportionnel à l'inverse du nombre d'itérations $ t $, et l'inverse de $ E (\ alpha, \ beta) $ à ce point est également multiplié. J'ai essayé d'utiliser celui-là. Il semble qu'il n'y ait pas d'autre choix que de faire des essais et des erreurs sur la façon de déterminer ce taux d'apprentissage et cette valeur initiale, mais si quelqu'un connaît un bon moyen de le rechercher, je vous serais reconnaissant de bien vouloir me le dire. Si vous vous trompez un peu, les points voleront hors du cadre et ne reviendront pas (rires).
Puisque la fonction d'erreur qui détermine le gradient dépend du nombre aléatoire, on peut voir qu'elle change à chaque fois. La droite de régression est également assez violente au début, mais on voit qu'elle devient progressivement plus silencieuse et converge.
 Le code est ici.
Le code est ici.
Pour être honnête, l'exemple d'animation ci-dessus est pour celui avec une meilleure convergence, et le graphique ci-dessous montre la convergence de $ \ alpha $ et $ \ beta $ lorsqu'il est répété 10000 fois, mais $ \ alpha $ s'approche de la vraie valeur de 1, mais $ \ beta $ converge autour de 0,5 et il est peu probable qu'il s'approche davantage de la vraie valeur de 0.

Cela semble être dû aux caractéristiques de la fonction d'erreur de la droite de régression cette fois, mais comme vous pouvez le voir sur le graphique ci-dessous, pour $ \ alpha $, la courbe minimale est d'environ $ \ alpha = 1 $. Il est tombé autour de la valeur. Cependant, comme il n'y a que des changements très progressifs dans les lignes verticales, il est difficile d'obtenir un gradient qui provoque un mouvement vertical. S'il s'agit de la méthode de descente la plus raide normale, etc., cette surface courbe elle-même ne change pas, nous visons donc la valeur minimale doucement le long de la vallée, mais en premier lieu, car cette surface courbe change à chaque fois, dans la direction de $ \ beta $ Il ne semble y avoir aucun mouvement.

Maintenant, aviez-vous une image de la méthode de descente de gradient stochastique? J'ai obtenu une image en dessinant ce graphique d'animation. Le code python qui dessine l'animation de cette méthode de descente de gradient probabiliste peut être trouvé à ici, alors essayez-le si vous le souhaitez. S'il vous plaît essayez.
(Supplément) Trouvez les paramètres de la droite de régression par la méthode la plus probable
y_n = f(x_n, \alpha, \beta) + \epsilon_n (n =1,2,...,N)
Autrement dit, l'erreur est
\epsilon_n = y_n - f(x_n, \alpha, \beta) (n =1,2,...,N) \\
\epsilon_n = y_n -\alpha x_n - \beta
Peut être représenté par. Si cette erreur $ \ epsilon_i $ suit une distribution normale avec moyenne = 0, variance = $ \ sigma ^ 2 $, la probabilité de la fonction d'erreur est
L = \prod_{n=1}^{N} \frac{1}{\sqrt{2\pi\sigma^2}} \exp \left( -\frac{\epsilon_n^2}{2\sigma^2} \right)
Et si vous prenez le logarithme
\log L = -\frac{N}{2} \log (2\pi\sigma^2) -\frac{1}{2\sigma^2} \sum_{n=1}^{N} \epsilon_n^2
Et si vous ne récupérez que les termes qui dépendent des paramètres $ \ alpha, beta $
l(\alpha, \beta) = \sum_{n=1}^{N} \epsilon_n^2 = \sum_{n=1}^{N} (y_n -\alpha x_n - \beta)^2
Vous pouvez voir que vous devez minimiser. Utilisez ceci comme une fonction d'erreur
E({\bf w})=\sum_{n=1}^{N} E_n({\bf w}) = \sum_{n=1}^{N} (y_n -\alpha x_n - \beta)^2 \\
{\bf w} = (\alpha, \beta)^{\rm T}
Il est exprimé comme.
Recommended Posts