Résumé des fonctions d'activation (step, sigmoïde, ReLU, softmax, fonction constante)

[Référence] [Deep Learning from scratch](https://www.amazon.co.jp/%E3%82%BC%E3%83%AD%E3%81%8B%E3%82%89%E4% BD% 9C% E3% 82% 8BApprentissage en profondeur-% E2% 80% 95Python% E3% 81% A7% E5% AD% A6% E3% 81% B6% E3% 83% 87% E3% 82% A3% E3 % 83% BC% E3% 83% 97% E3% 83% A9% E3% 83% BC% E3% 83% 8B% E3% 83% B3% E3% 82% B0% E3% 81% AE% E7% 90 % 86% E8% AB% 96% E3% 81% A8% E5% AE% 9F% E8% A3% 85-% E6% 96% 8E% E8% 97% A4-% E5% BA% B7% E6% AF % 85 / dp / 4873117585)

Quelle est la fonction d'activation?

La fonction d'activation est chargée de déterminer comment la somme des signaux d'entrée est activée. Cela sert d'arrangement pour les valeurs passées à la couche suivante.

Typiquement, Dans la fonction d'activation de "perceptron simple", des "fonctions d'étape", etc. sont utilisées, Dans la fonction d'activation du "perceptron multicouche (réseau neuronal)", "la fonction sigmoïde, la fonction softmax" et la fonction d'équivalence sont utilisées. De plus, alors que ces «fonctions pas à pas, fonction sigmoïde, fonction softmax» sont appelées fonctions non linéaires, les fonctions telles que «y = cx» sont appelées fonctions linéaires. En général, les réseaux de neurones n'utilisent pas de fonctions linéaires. La raison en est "[Pourquoi ne pas utiliser des fonctions linéaires avec le perceptron multicouche?](Https://qiita.com/namitop/items/d3d5091c7d0ab669195f#%E3%81%AA%E3%81%9C%E5%A4%" 9A% E5% B1% A4% E3% 83% 91% E3% 83% BC% E3% 82% BB% E3% 83% 97% E3% 83% 88% E3% 83% AD% E3% 83% B3% E3% 81% A7% E7% B7% 9A% E5% BD% A2% E9% 96% A2% E6% 95% B0% E3% 82% 92% E4% BD% BF% E3% 82% 8F% E3% 81% AA% E3% 81% 84% E3% 81% AE% E3% 81% 8B) ». En général, les fonctions softmax et d'équivalence sont utilisées dans la couche de sortie.

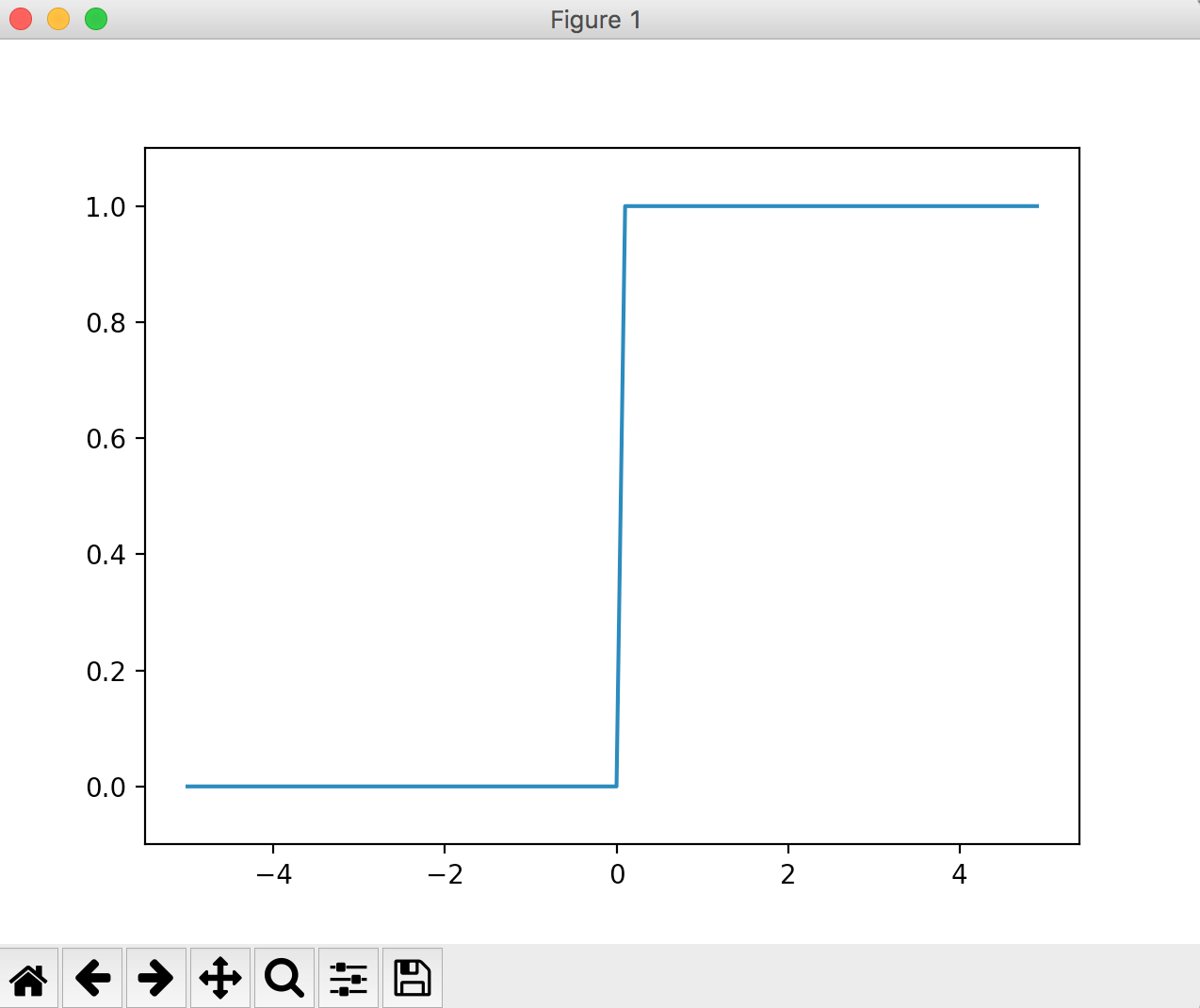
Fonction Step

La fonction pas à pas est une fonction qui commute la sortie au seuil. Aussi connu sous le nom de "fonction d'escalier". Cette fonction est généralement utilisée dans les perceptrons simples (réseaux monocouche).

Par exemple, une fonction pas à pas qui devient 0 lorsque la valeur saisie est égale ou inférieure à 0 et 1 lorsqu'elle est supérieure à 0 La mise en œuvre et le fonctionnement sont indiqués ci-dessous.

def step_function(x):
  if x>0:
    return 1
  else:
    return 0

# step_function(4) => 1
# step_function(-3) => 0

Le graphique peut être implémenté comme suit. step_function est implémentée pour pouvoir gérer le tableau [np.array ()] comme argument. Le comportement est le même, sauf pour la gestion des tableaux.

import numpy as np
import matplotlib.pylab as plt

def step_function(x):
  y = x > 0
  return y.astype(np.int)

x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

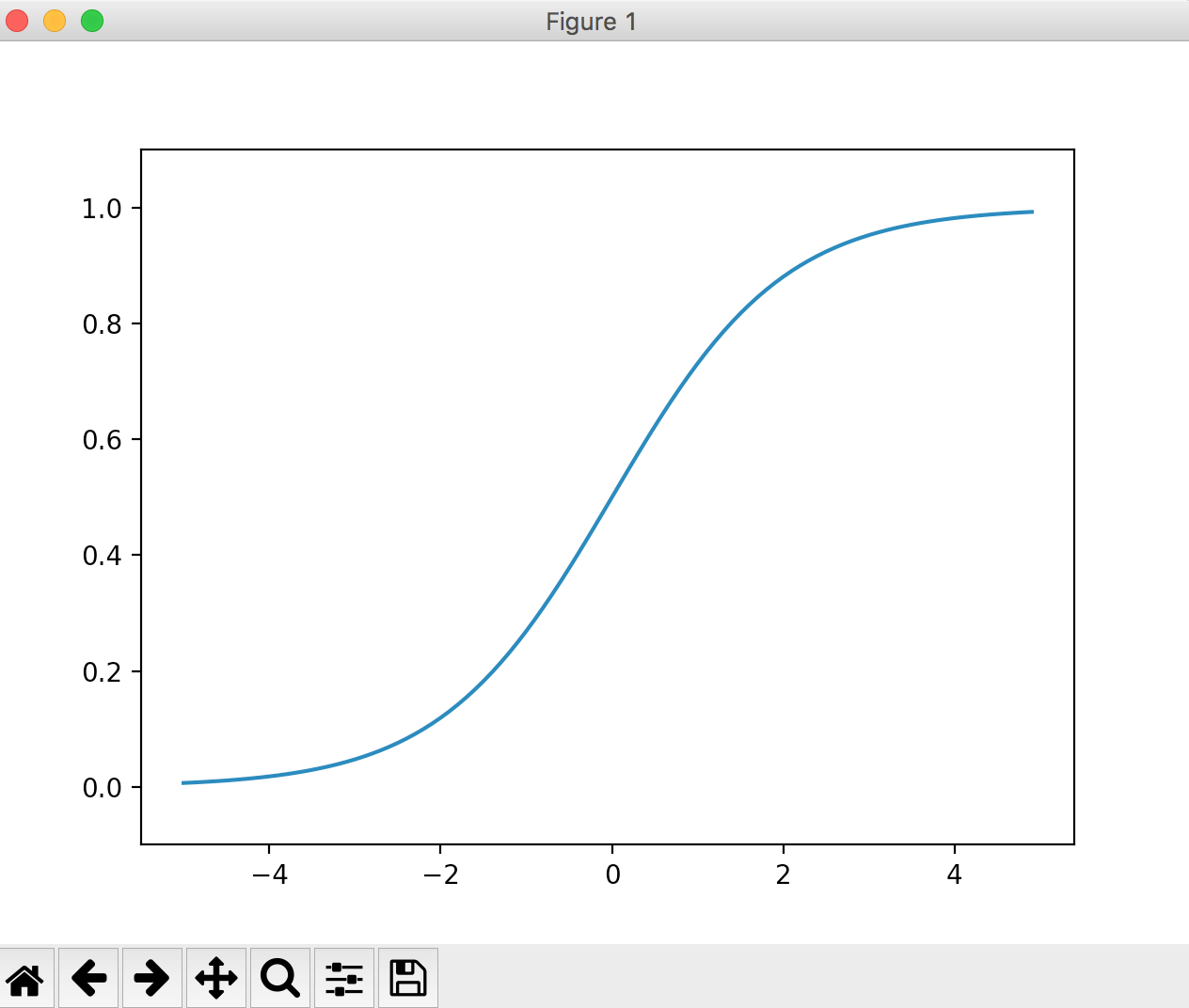
Fonction Sigmaid

La formule est la suivante.

h(x) = \frac{1}{1+e^{-x}}\\
e^{-x}Est np dans numpy.exp(-x)Peut être écrit.

Plus la valeur que vous entrez est élevée, plus proche de 1 Plus la valeur que vous entrez est petite, plus elle est proche de 0. On peut dire que la sortie de la fonction step ne tue pas trop la valeur de l'entrée d'origine par rapport à 0 ou 1.

La mise en œuvre et le fonctionnement sont les suivants.

import numpy as np

def sigmoid(x):
  return 1 / (1+np.exp(-x))

x = np.array([-3.0, 1.0, 4.0])
# sigmoid(x) => [ 0.04742587  0.73105858  0.98201379]

Le graphique ressemble à ceci:

import numpy as np
import matplotlib.pylab as plt

def sigmoid(x):
  return 1 / (1+np.exp(-x))

x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

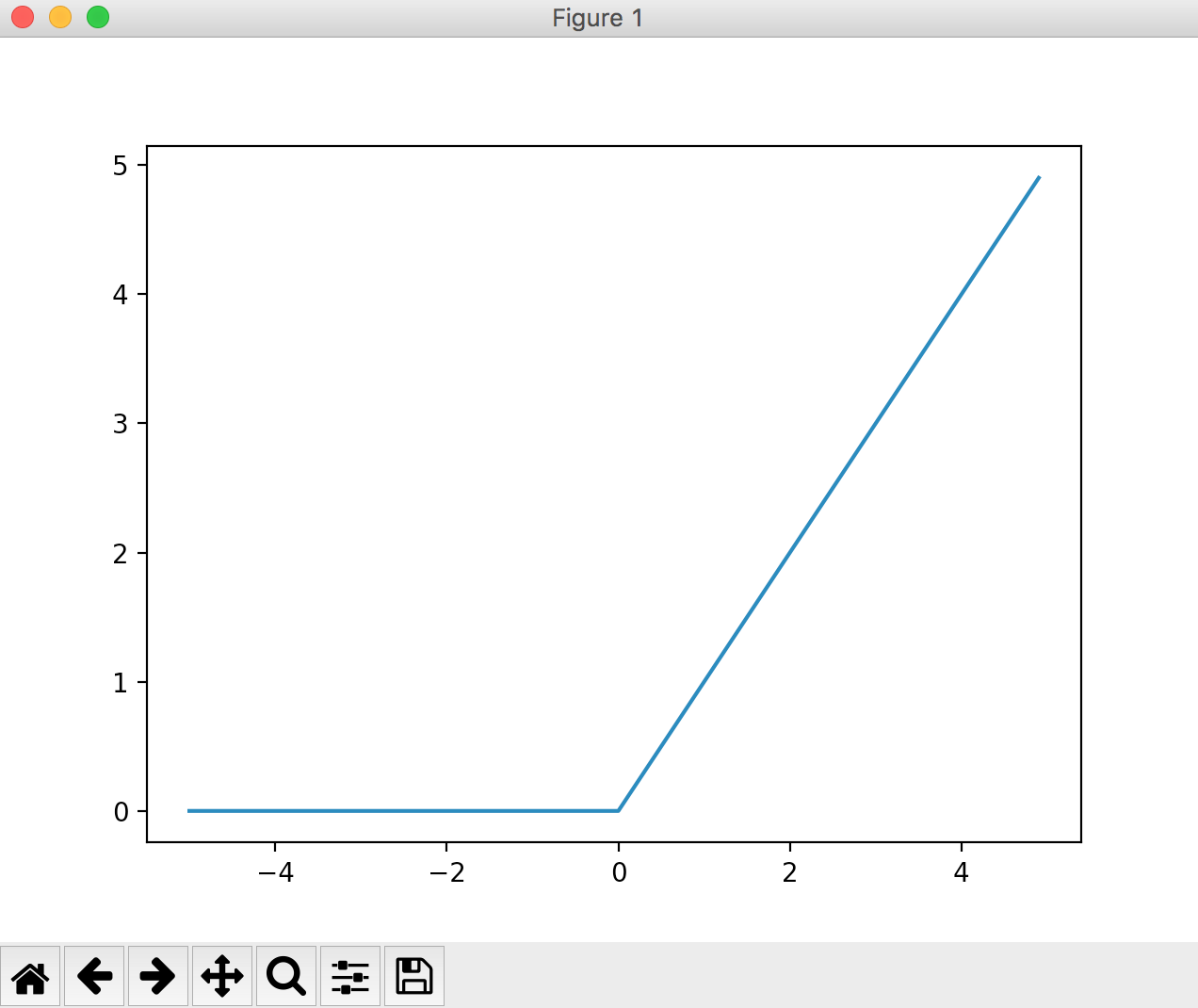
Fonction ReLU

Lorsque la valeur d'entrée est égale ou inférieure à 0, elle devient 0, et lorsqu'elle est supérieure à 1, l'entrée est sortie telle quelle. Le graphique ressemblera à celui ci-dessous.

import numpy as np
import matplotlib.pylab as plt

def relu(x):
  return np.maximum(0, x)

x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.show()

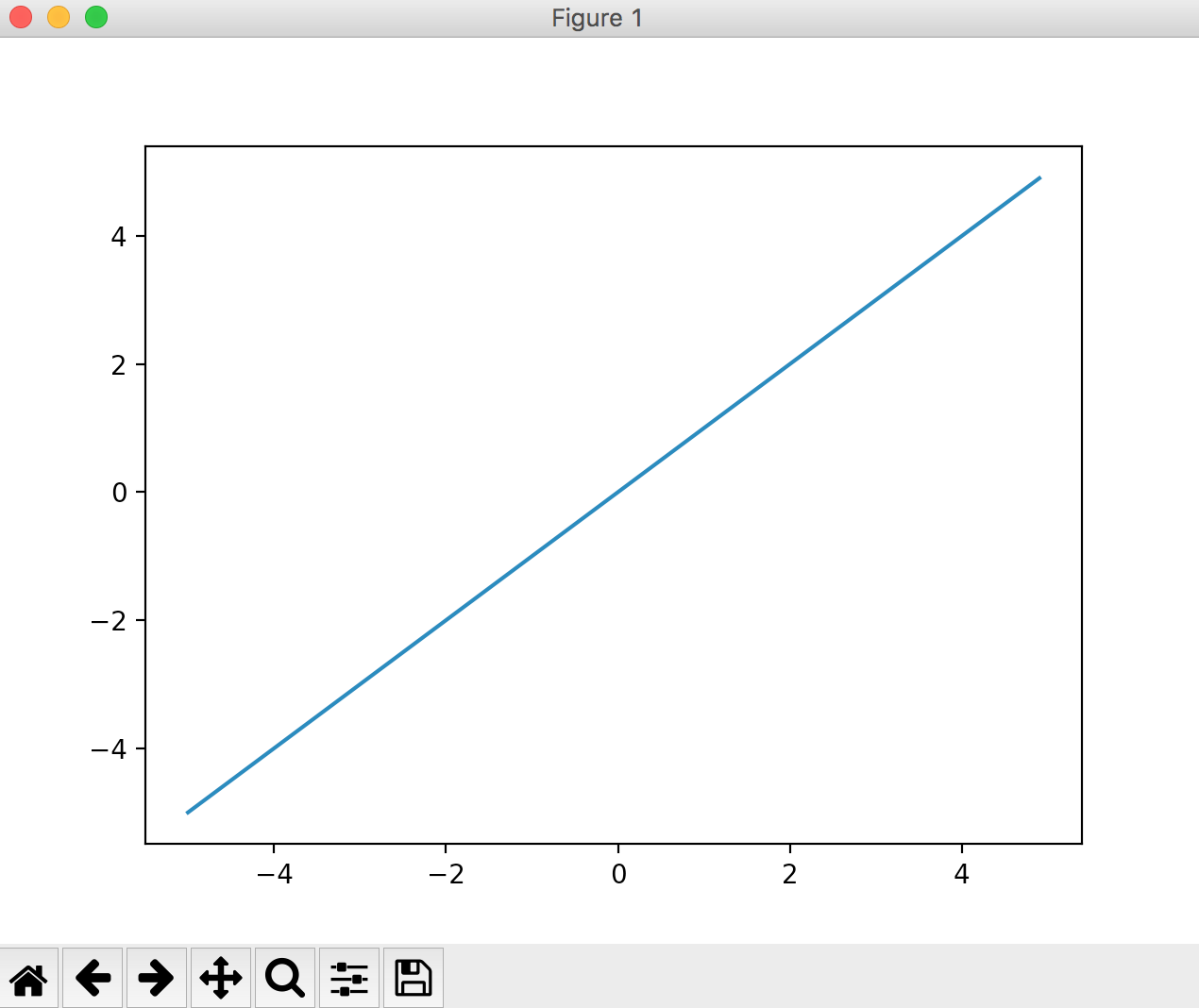
Fonction égale

Une fonction utilisée dans la couche de sortie. Une fonction qui renvoie toujours la même valeur que la valeur saisie. [Question] Mathématiques: Qu'est-ce qu'une fonction égale

Couramment utilisé dans les problèmes de régression.

import numpy as np
import matplotlib.pylab as plt

def koutou(a):
  return a

x = np.arange(-5, 5, 0.1)
y = koutou(x)
plt.plot(x, y)
plt.show()

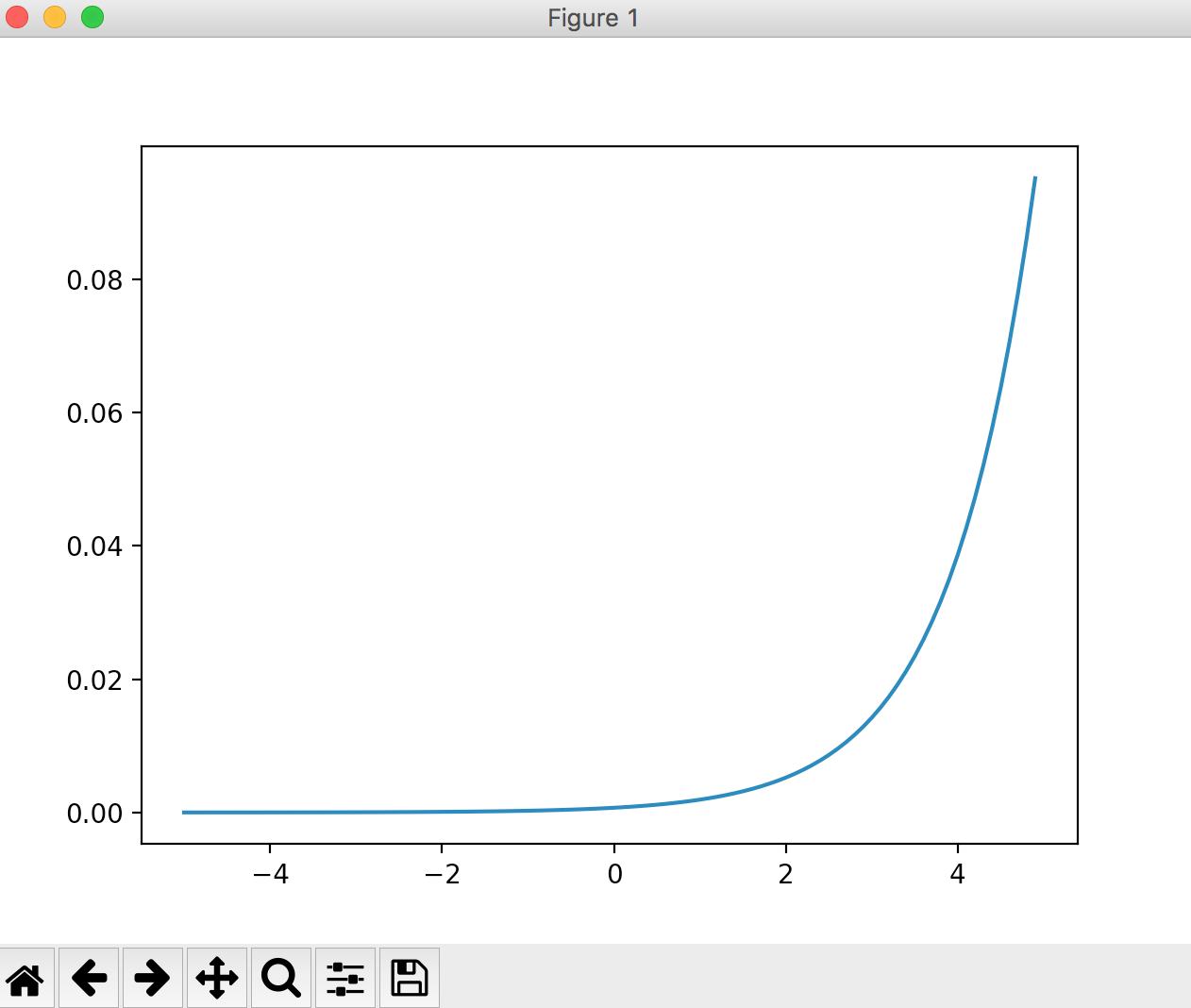
Fonction Softmax

Une fonction utilisée dans la couche de sortie. Couramment utilisé dans les problèmes de classification.

import numpy as np
import matplotlib.pylab as plt

def softmax(a):
  exp_a = np.exp(a)
  sum_exp_a = np.sum(exp_a)
  y = exp_a / sum_exp_a
  return y

x = np.arange(-5, 5, 0.1)
y = softmax(x)
plt.plot(x, y)
plt.show()

Fonctions linéaires et non linéaires

Une fonction linéaire est une fonction dont la sortie est un multiple constant de l'entrée. Par exemple, y = cx (c est une constante). Si vous faites un graphique, ce sera une ligne droite.

Les fonctions non linéaires sont celles qui ne sont pas des fonctions linéaires.

Pourquoi ne pas utiliser des fonctions linéaires dans les perceptrons multicouches?

La raison en est que l'utilisation d'une fonction linéaire comme fonction d'activation rend inutile l'approfondissement de la couche dans un réseau neuronal. Le problème avec les fonctions linéaires est dû au fait que quelle que soit la profondeur des couches, il y aura toujours un "réseau sans couches cachées" qui fera la même chose. A titre d'exemple simple, si vous empilez trois couches avec la fonction linéaire h (x) = cx comme fonction d'activation, vous obtenez y = h (h (h (x)). Autrement dit, c'esty = c * Il peut être exprimé même dans un réseau sans couche cachée comme c * c * x (y = ax).

Si vous utilisez une fonction linéaire pour la fonction d'activation comme dans cet exemple, vous ne pouvez pas profiter de plusieurs couches. En d'autres termes, vous ne devez pas utiliser de fonctions linéaires pour les fonctions d'activation, car cela peut entraîner un traitement inutile.

Problème de régression et problème de classification

Le problème de la régression est le problème de la réalisation de prédictions numériques (continues) à partir de certaines données d'entrée. (Exemple: Le problème de la prédiction du poids d'une personne à partir d'une image de la personne)

Le problème de classification est la question de savoir à quelle classe les données appartiennent. (Exemple: un problème qui classe une personne comme homme ou femme à partir d'une image d'une personne)