 | Introduction à la physique computationnelle
(2000 / 12)
Harvey Gold, Jant Bochinik, etc.
Afficher les détails du produit
C'est en rapport avec.
Beaucoup de choses qui se développent en ajoutant au hasard des unités de base au monde naturel, telles que la formation de fissures en forme d'éclair dans les cristaux de neige et les failles géologiques, et la croissance de colonies bactériennes, peuvent être observées. L'un des modèles bien connus est l'agrégation à diffusion limitée (DLA). Ce modèle est un exemple de la façon dont des mouvements aléatoires produisent de beaux groupes auto-similaires.
Les étapes de la croissance des clusters sont
- Un type de particule occupe un point de réseau
- Émettez une particule autour du cercle autour de la graine
- Parcourez les particules au hasard
- Lorsque vous atteignez un point autour d'un, il y adhère → Aller à 2
Répétez ce processus jusqu'à ce qu'un grand cluster soit formé (généralement des milliers à des millions de fois). De plus, afin de réduire la quantité de calcul, nous supprimerons les particules qui sont allées trop loin du cluster à l'étape 3 et recommencerons à partir de l'étape 2.
Pour réaliser réellement cette opération, nous pouvons voir qu'il suffit d'avoir une matrice qui représente la grille et un tableau qui enregistre les points autour des points de grille occupés. La partie de la marche aléatoire est détournée plusieurs fois, mais elle génère un nombre aléatoire uniforme et détermine la direction vers le haut, le bas, la gauche et la droite par l'ampleur de la valeur. De plus, dans la simulation réelle, la marche aléatoire à une position éloignée du cluster consomme la majeure partie du temps CPU et devient inefficace, alors essayez d'augmenter la longueur de foulée de la marche aléatoire à une position éloignée du cluster. C'était. Nous avons capturé la simulation réelle (création d'un cluster pour N = 200, 500, 1000), qui peut être confirmée ci-dessous.
http://youtu.be/qLii4DlBnv0
Je n'ai rien édité, donc c'est moche, mais w
a, b, c signifient a, b, c du problème du manuel, et a crée un cluster avec le nombre de particules spécifié dans la zone de saisie. b et c servent à trouver la probabilité d'adhésion par simulation de Monte Carlo et à trouver réellement la dimension fractale. Si vous êtes intéressé, veuillez vous référer au code source.
Les grappes obtenues lorsque N = 500 sont les suivantes.
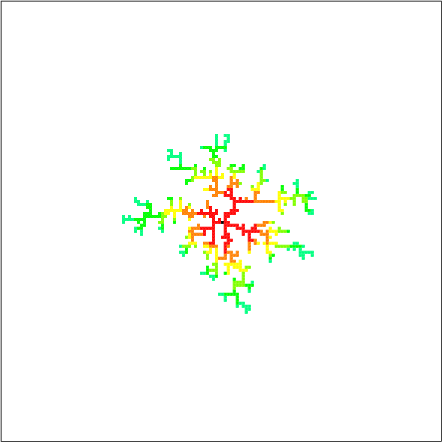
Lien ( Easy Chemical Experiment-Making a Beautiful Silver Tree </ strong>) Ne pensez-vous pas que cela ressemble beaucoup à l'image de Ginju dans un>)? En fait, puisque les marches aléatoires sont équivalentes à la diffusion, on peut dire que la simulation elle-même est entièrement basée sur la formation d'arbres métalliques, et bien sûr les formes des figures résultantes sont très similaires.
Le code source est répertorié ci-dessous.
La fonction pr pour enregistrer Canvas sera probablement utilisée fréquemment à l'avenir. SetParameter est également l'une des classes que j'utilise depuis longtemps. Je voudrais le résumer un peu plus, mais je n'ai pas de problème avec cela pour le moment, donc je pense que je vais continuer à l'utiliser pendant un moment.
DLA.py
#! /usr/bin/env python
# -*- coding:utf-8 -*-
#
# written by ssh0, August 2014.
from Tkinter import *
import numpy as np
import matplotlib.pyplot as plt
import random
import time
class DLA(object):
def __init__(self, N, view=True, color=True):
self.r = 3
self.N = N
self.view = view
self.color = color
self.L = int(self.N**(0.78))
if self.view:
self.default_size = 640 # default size of canvas
self.rsize = int(self.default_size/(2*self.L))
if self.rsize == 0:
self.rsize = 1
fig_size = 2*self.rsize*self.L
self.margin = 10
self.sub = Toplevel()
self.canvas = Canvas(self.sub, width=fig_size+2*self.margin,
height=fig_size+2*self.margin)
self.c = self.canvas.create_rectangle
self.update = self.canvas.update
self.sub.title('DLA cluster')
self.c(self.margin, self.margin,
fig_size+self.margin, fig_size+self.margin,
outline='black', fill='white')
self.canvas.pack()
self.start_time = time.time()
def grow_cluster(self):
lattice = np.zeros([self.L*2+1, self.L*2+1], dtype=int)
#Points de grille d'amorçage
self.center = self.L
lattice[self.center, self.center] = 1
if self.view:
c = self.c
rect = c((2*self.center-self.L)*self.rsize+self.margin,
(2*self.center-self.L)*self.rsize+self.margin,
(2*(self.center+1)-self.L)*self.rsize+self.margin-1,
(2*(self.center+1)-self.L)*self.rsize+self.margin-1,
outline='black', fill='black')
rn = np.random.rand
def reset():
"""Sélection du point initial"""
theta = 2*np.pi*rn()
x = int((self.r+2)*np.cos(theta))+self.center
y = int((self.r+2)*np.sin(theta))+self.center
return x, y
x, y = reset()
l = 1
n = 0
while n < self.N:
#Augmentez la foulée loin de la périphérie du cluster
r = np.sqrt((x-self.center)**2+(y-self.center)**2)
if r > self.r+2:
l = int(r-self.r-2)
if l == 0: l = 1
else:
l = 1
#Marche aléatoire
p = rn()*4
if p < 1:
x += l
elif p < 2:
x -= l
elif p < 3:
y += l
else:
y -= l
r = np.sqrt((x-self.center)**2+(y-self.center)**2)
#Refaire le processus à un point éloigné du point central
if r >= 2*self.r:
x, y = reset()
continue
judge = np.sum(lattice[x-1,y]+lattice[x+1,y]
+lattice[x,y-1]+lattice[x,y+1])
#Apportez des particules dans un cluster
if judge > 0:
lattice[x, y] = 1
#dessin
if self.view:
if self.color:
colors = ['#ff0000', '#ff8000', '#ffff00', '#80ff00',
'#00ff00', '#00ff80', '#00ffff', '#0080ff',
'#0000ff', '#8000ff', '#ff00ff', '#ff0080']
color = colors[int(n/100)%len(colors)]
else:
color = "black"
rect = c((2*x-self.L)*self.rsize+self.margin,
(2*y-self.L)*self.rsize+self.margin,
(2*(x+1)-self.L)*self.rsize+self.margin-1,
(2*(y+1)-self.L)*self.rsize+self.margin-1,
outline=color, fill=color)
self.update()
#mise à jour rmax
if int(r)+1 > self.r:
self.r = int(r) + 1
x, y = reset()
n += 1
else:
if self.view:
self.end_time = time.time()
t = self.end_time-self.start_time
print "done; N = %d, time = " % self.N + str(t) + ' (s)'
return lattice
class SetParameter():
def show_setting_window(self, parameters, commands):
""" Show a parameter setting window.
parameters: A list of dictionaries {'parameter name': default_value}
commands: A list of dictionary {'name of button': command}
"""
self.root = Tk()
self.root.title('Parameter')
frame1 = Frame(self.root, padx=5, pady=5)
frame1.pack(side='top')
self.entry = []
for i, parameter in enumerate(parameters):
label = Label(frame1, text=parameter.items()[0][0] + ' = ')
label.grid(row=i, column=0, sticky=E)
self.entry.append(Entry(frame1, width=10))
self.entry[i].grid(row=i, column=1)
self.entry[i].delete(0, END)
self.entry[i].insert(0, parameter.items()[0][1])
self.entry[0].focus_set()
frame2 = Frame(self.root, padx=5, pady=5)
frame2.pack(side='bottom')
self.button = []
for i, command in enumerate(commands):
self.button.append(Button(frame2, text=command.items()[0][0],
command=command.items()[0][1]))
self.button[i].grid(row=0, column=i)
self.root.mainloop()
class Main(object):
def __init__(self):
import sys
self.sp = SetParameter()
self.dla = None
self.b = None
self.sp.show_setting_window([{'N': 200}],
[{'a': self.exp_a},
{'b': self.exp_b},
{'c': self.exp_c},
{'c:fit': self.fitting},
{'save': self.pr},
{'quit': sys.exit}])
def exp_a(self):
self.N = int(self.sp.entry[0].get())
self.dla = DLA(self.N)
lattice = self.dla.grow_cluster()
def exp_b(self):
trial = 3000
self.dla2 = DLA(2, view=False)
self.dla2.L = 6
distribution = {'p': 0, 'q': 0, 'r': 0, 's': 0}
#Classification
for i in range(trial):
lattice = self.dla2.grow_cluster()
l = lattice[self.dla2.L-1:self.dla2.L+2,
self.dla2.L-1:self.dla2.L+2]
if np.sum(l) == 2:
distribution['r'] += 1
elif np.sum(l[0,1]+l[1,0]+l[1,2]+l[2,1]) == 1:
distribution['p'] += 1
elif max(max(np.sum(l, 0)), max(np.sum(l, 1))) == 3:
distribution['s'] += 1
else:
distribution['q'] += 1
for k, v in distribution.items():
distribution[k] = float(v)/trial
distribution['p'] = distribution['p']/2.
distribution['q'] = distribution['q']/2.
print 'trial = %d' % trial
print distribution
def exp_c(self):
self.N = int(self.sp.entry[0].get())
self.dla3 = DLA(self.N, view=False)
self.lattice = self.dla3.grow_cluster()
self.view_expansion()
self.plot()
def view_expansion(self):
lattice = self.lattice
center = self.dla3.center
M_b = []
s = np.sum
ave = np.average
append = M_b.append
for k in range(1, center):
nonzero = np.nonzero(lattice[k:-k,k:-k])
tmp = np.array([0])
for i, j in zip(nonzero[0]+k, nonzero[1]+k):
tmp = np.append(tmp, s(lattice[i-k:i+k+1, j-k:j+k+1]))
append(ave(tmp))
self.b = np.array([2.*k+1 for k in range(1, center)])
self.M_b = np.array(M_b)
def plot(self):
fig = plt.figure("Fractal Dimension")
self.ax = fig.add_subplot(111)
self.ax.plot(self.b, self.M_b, '-o')
self.ax.set_xlabel(r'$b$', fontsize=16)
self.ax.set_ylabel(r'$M(b)$', fontsize=16)
self.ax.set_xscale('log')
self.ax.set_yscale('log')
self.ax.set_ymargin(0.05)
fig.tight_layout()
plt.show()
def fitting(self):
if self.b == None:
return
import scipy.optimize as optimize
def fit_func(parameter0, b, M_b):
log = np.log
c1 = parameter0[0]
c2 = parameter0[1]
residual = log(M_b) - c1 - c2*log(b)
return residual
def fitted(b, c1, D):
return np.exp(c1)*(b**D)
cut_from = int(raw_input("from ? (index) >>> "))
cut_to = int(raw_input("to ? (index) >>> "))
cut_b = np.array(list(self.b)[cut_from:cut_to])
cut_M_b = np.array(list(self.M_b)[cut_from:cut_to])
parameter0 = [0.1, 2.0]
result = optimize.leastsq(fit_func, parameter0, args=(cut_b, cut_M_b))
c1 = result[0][0]
D = result[0][1]
self.ax.plot(cut_b, fitted(cut_b, c1, D),
lw=2, label="fit func: D = %f" % D)
plt.legend(loc='best')
plt.show()
def pr(self):
import tkFileDialog
import os
if self.dla is None:
print "first you should run 'a'."
return
fTyp=[('eps flle','*.eps'), ('all files','*')]
filename = tkFileDialog.asksaveasfilename(filetypes=fTyp,
initialdir=os.getcwd(),
initialfile="figure_1.eps")
if filename == None:
return
self.dla.canvas.postscript(file=filename)
if __name__ == '__main__':
Main()
|

