Première régression TensorFlow-Linear en guise d'introduction
** (Ajout: j'ai publié un article révisé --http: //qiita.com/TomokIshii/items/0a7041ad337f68f71286) **
La semaine dernière (9 novembre 2015), le Framework de Deep Learnin "TensorFlow" a été publié, mais j'étais convaincu que l'explication du document "MNIST (classification des nombres manuscrits) est" Hello World "de l'apprentissage automatique." Je ne peux pas. Comme ce fut le cas avec le Machine Learning de Coursera (Stanford), lors de l'apprentissage de l'apprentissage automatique depuis le début, je le considère personnellement comme une régression linéaire au début.
Dans cet article, nous allons d'abord examiner le code de la régression linéaire, puis créer le code de la régression logistique pour avoir une idée de TensorFlow.
Régression linéaire
Concernant "Theano", qui est le précurseur de TensorFlow (sorti en premier), le code Newmu Theano-Tutorials est publié sur GitHub en plus du tutoriel du document original. (https://github.com/Newmu/Theano-Tutorials)
Un code court est affiché afin que vous puissiez avoir une meilleure compréhension de "Theano" étape par étape. 1_linear_regression.py (code pour la régression linéaire) est posté après 0_multiply.py (multiplication), mais nous allons créer le code pour la version TensorFlow basé sur cette version Theano.
La première est la version Theano du code.
#Définition de variable symbolique"T"Est theano.Remplacement du tenseur
X = T.scalar()
Y = T.scalar()
def model(X, w):
return X * w
#Déclaration des variables partagées
w = theano.shared(np.asarray(0., dtype=theano.config.floatX))
y = model(X, w)
#Définition du graphe
cost = T.mean(T.sqr(y - Y))
gradient = T.grad(cost=cost, wrt=w)
updates = [[w, w - gradient * 0.01]]
#une fonction
train = theano.function(inputs=[X, Y], outputs=cost, updates=updates, allow_input_downcast=True)
#Apprentissage par calcul de boucle
for i in range(100):
for x, y in zip(trX, trY):
train(x, y)
Ensuite, examinons de plus près la version de TensorFlow.
Tout d'abord, après avoir importé les modules associés, préparez les données à utiliser. (La version Theano était des données de test sans section b, mais ici elle est incluse b (= 3.0).)
import numpy as np
import tensorflow as tf
trX = np.linspace(-1, 1, 101)
trY = 2 * trX + 3 + np.random.randn(*trX.shape) * 0.33
def lin_model(X, w, b):
return X * w + b
lin_model () est une fonction utilisée comme modèle de régression. (Fonction linéaire avec la pente w et la section b comme paramètres.)
Ensuite, préparez les variables nécessaires.
w = tf.Variable([0.])
b = tf.Variable([0.])
x = tf.placeholder(tf.float32, shape=(101))
y = tf.placeholder(tf.float32, shape=(101))
w et b sont des variables ordinaires. La valeur initiale a été définie sur [0.]. Bien que x et y soient des termes propres à TensorFlow (terminologie), ils sont préparés comme des espaces réservés. Puisqu'il s'agit d'un espace réservé, il n'y a pas de valeur réelle au moment de la déclaration et la valeur réelle sera affectée dans le traitement du programme suivant.
Ensuite, nous décrivons la relation importante entre les variables appelées Graph.
y_hypo = lin_model(x, w, b)
cost = tf.reduce_mean(tf.square(y_hypo - y))
Le coût est une fonction de coût qui correspond à la différence entre votre modèle et les données réelles. "tf.reduce_mean ()" est une fonction pour calculer la moyenne. (Je pense que "mean ()" est bien, mais dans TensorFlow, c'est "reduction_mean ()" pour une raison quelconque ... Il semble que ce soit dans le groupe de fonctions de réduction.)
Définissez ensuite la spécification de l'Optimiseur et sa méthode de calcul de la recherche de paramètre.
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
Ici, l'optimiseur de la méthode de descente de gradient est spécifié, et le taux d'apprentissage de 0,01 est donné en argument.
À propos de l'Optimizer
Maintenant, je suis curieux d'Optimizer, mais TensorFlow prend actuellement en charge ce qui suit. http://www.tensorflow.org/api_docs/python/train.html#optimizers
| Optimizer name | Description |
|---|---|
| GradientDescentOptimizer | Optimiseur par méthode de descente de gradient |
| AdagradOptimizer | Optimiseur par la méthode AdaGrad |
| MomentumOptimizer | Optimiseur de méthode Momentum |
| AdamOptimizer | Méthode Adam (Ceci est également célèbre.) |
| FtrlOptimizer | (Je l'ai entendu pour la première fois)"Follow the Regularized Leader"algorithme |
| RMSPropOptimizer | (Je l'ai entendu pour la première fois) Un algorithme qui automatise l'ajustement du taux d'apprentissage |
Les paramètres qui doivent être définis diffèrent en fonction de l'optimiseur, mais cette fois, nous utiliserons le GradientDescentOptimizer de base. (Le taux d'apprentissage des paramètres requis a été défini comme décrit ci-dessus.)
Régression linéaire (suite)
Maintenant que nous sommes presque prêts, nous commençons une session qui montre la partie principale du calcul. Cependant, les variables (Variables) doivent être initialisées avant de démarrer la Session. Ceci est propre à "Tensor Flow", qui n'était pas dans "Theano".
# Initializing
init = tf.initialize_all_variables()
"Initialiser les variables avant le début d'une session" semble être une règle souvent oubliée. Pour le moment, si vous cochez
- La variable de tf.Variable () doit être initialisée **.
- La variable de tf.placeholder () est initialisée ** inutile **. (Il sera attribué à l'entité plus tard)
- Les variables (constantes) de tf.constant ne sont pas initialisées **. Il est dit que. Dans la liste ci-dessus, les variables sont initialisées à l'aide de initialize_all_variable ().
La partie Session est la suivante.
# Train
with tf.Session() as sess:
sess.run(init)
for i in range(1001):
sess.run(train_step, feed_dict={x: trX, y: trY})
if i % 100 == 0:
print "%5d:(w,b)=(%10.4f, %10.4f)" % (i, sess.run(w), sess.run(b))
Il semble y avoir plusieurs façons d'écrire un programme pour exécuter Sessoin, mais comme mentionné ci-dessus, le délimiteur de session est clarifié en le plaçant dans l'instruction "with", et il est automatiquement ouvert lorsque le "with" est quitté. La session est fermée (), ce qui est pratique.
La première est qu'il est difficile de fournir des données Train dans TensorFlow. L'alimentation des données est une partie où le traitement change en fonction de la façon dont vous procédez à l'apprentissage, mais comme indiqué dans la liste ci-dessus, "feed-dict" sera utilisé, alors gardez à l'esprit. (J'étudie toujours cette partie ...)
Avec ce qui précède, les paramètres de régression sont calculés. (On montre comment il est utilisé pour les vraies valeurs w = 2,0 et b = 3,0.)
0:(w,b)=( 0.0135, 0.0599)
100:(w,b)=( 0.9872, 2.6047)
200:(w,b)=( 1.4793, 2.9421)
300:(w,b)=( 1.7280, 2.9869)
400:(w,b)=( 1.8538, 2.9928)
500:(w,b)=( 1.9173, 2.9936)
600:(w,b)=( 1.9494, 2.9937)
700:(w,b)=( 1.9657, 2.9937)
800:(w,b)=( 1.9739, 2.9937)
900:(w,b)=( 1.9780, 2.9937)
1000:(w,b)=( 1.9801, 2.9937)
Ce qui précède est résumé et le programme est à nouveau affiché. (C'est devenu un programme d'environ 30 lignes.)
import numpy as np
import tensorflow as tf
trX = np.linspace(-1, 1, 101)
trY = 2 * trX + 3 + np.random.randn(*trX.shape) * 0.33
def lin_model(X, w, b):
return X * w + b
w = tf.Variable([0.])
b = tf.Variable([0.])
x = tf.placeholder(tf.float32, shape=(101))
y = tf.placeholder(tf.float32, shape=(101))
y_hypo = lin_model(x, w, b)
cost = tf.reduce_mean(tf.square(y_hypo - y))
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
# Initializing
init = tf.initialize_all_variables()
# Train
with tf.Session() as sess:
sess.run(init)
for i in range(1001):
sess.run(train_step, feed_dict={x: trX, y: trY})
if i % 100 == 0:
print "%5d:(w,b)=(%10.4f, %10.4f)" % (i, sess.run(w), sess.run(b))
À propos de la session interactive
La liste ci-dessus est un programme qui exécute Session comme traitement par lots (quoique court). En dehors de cela, TensorFlow prend en charge une fonction appelée Session interactive, qui, comme son nom l'indique, vous permet de vous déplacer de manière interactive. http://tensorflow.org/get_started/basic_usage.html#interactive-usage
Cela signifie que cela fonctionne bien avec IPython, c'est-à-dire que cela fonctionne bien avec Jupyter Notebook, donc je l'ai immédiatement essayé.
(C'est comme ça...)
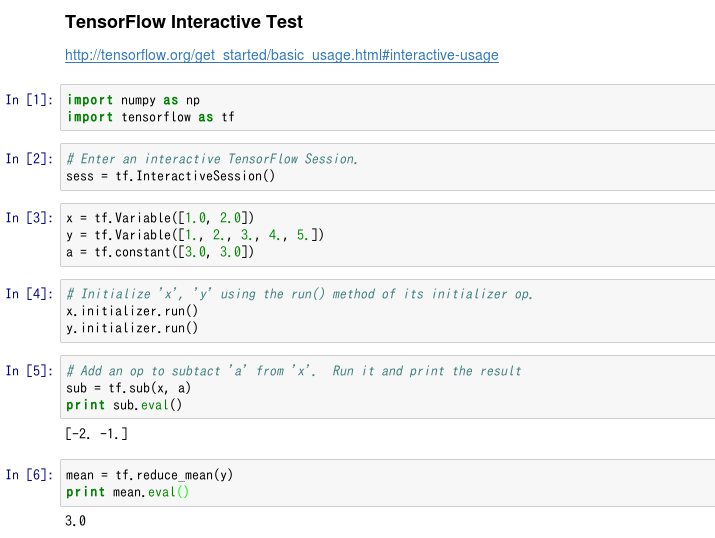
Ce type d'utilisation semble être pratique lorsque vous essayez d'étudier TensorFlow à partir de maintenant. (Au contraire, cette session interactive n'est pas adaptée au cas de l'exécution d'un programme pendant une longue période.)
Régression logistique
Sur la base du code de régression linéaire ci-dessus, nous avons créé le code de régression logistique. Notez que ce code est pour la classification à 2 classes, pas pour les multi-classes. (Comme vous le savez, MNIST utilise la régression Softmax, qui résout le problème de la classification multiclasse (10 classes).)
def lin_model(X, w, b):
return X * w + b
w = tf.Variable([0.])
b = tf.Variable([0.])
x = tf.placeholder(tf.float32, shape=(mlen))
y = tf.placeholder(tf.float32, shape=(mlen))
p_1 = lin_model(x, w, b)
x_entropy = tf.nn.sigmoid_cross_entropy_with_logits(p_1, y, name='xentropy')
loss = tf.reduce_mean(x_entropy, name='xentropy_mean')
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(loss)
Dans la régression linéaire, la fonction de coût définie par l'erreur quadratique moyenne (MSE) est remplacée par l'entropie croisée dans la régression logistique. "Tf.nn.sigmoid_cross_entropy_with_logits ()" dans la seconde moitié de la liste ci-dessus est une fonction qui calcule l'entorpie croisée. ("TensorFlow" a de nombreuses fonctions au nom long ...)
L'initialisation des variables et la façon de procéder avec Session sont les mêmes que dans le code précédent.
Jusqu'à présent, nous avons vu les codes de régression linéaire et de régression logistique. À ce stade, je pense que nous pouvons commencer à travailler sur du code MLP (Multi Layer Perceptron) (par exemple, MNIST) en douceur.
Références (site Web)
- TensorFlow web site http://www.tensorflow.org/
- Newmu Theano-Tutorials - GitHub https://github.com/Newmu/Theano-Tutorials
- Essayer la régression avec TensorFlow --Qiita http://qiita.com/syoamakase/items/db883d7ebad7a2220233 --Profitez deux fois du matériel Coursera / Machine Learning --Qiita http://qiita.com/TomokIshii/items/b22a3681cb17836c8f6e
(Note) Le document TenforFlow semble être mis à jour fréquemment, probablement parce que la version est encore peu profonde. Veuillez me pardonner si le lien est rompu.