Introduction to Programming for College Students: Various Functions Related to Rectangle (Part 2)
- With Qiita, it is difficult to print only the text part. Therefore, the same content is posted on the following page. If you want to print out or convert to PDF, please use this page:
http://gurakura.sakura.ne.jp/hellomondrian/rect3/
Click here for a list: http://gurakura.sakura.ne.jp/series/美大生のためのプログラミング入門/
Qiita version general table of contents: https://qiita.com/iigura/items/37180d127da93d0b8abb
How to draw a non-free rectangle
Now, this section concludes by introducing how to draw a non-free quadrangle as opposed to a free quadrangle. I think there are various definitions of inconvenient quadrilaterals, but here I would like to take up squares as quadrilaterals with less freedom, which have the same shape (= similar figures) no matter who draws them.
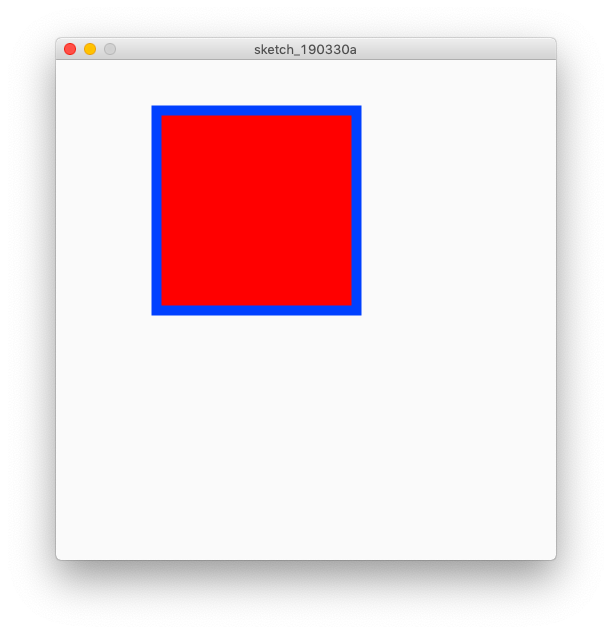
Draw a square with the square function. The argument is square (x, y, l). x and y are the upper left positions of the square, and l is the length of the side.
Remarks: By the way, the reference position indicated by (x, y) can be changed with the rectMode function.
background(250,250,250);
size(500,500);
strokeWeight(10);
stroke(0,64,255);
fill(255,0,0);
square(100,50,200);
Column: Relationship between quad, rect, square
You can use the quad function to represent a rect function. You can also use the rect function to represent a square function. The rectangle drawn by rect (x, y, w, h) has vertices (x, y), (x + w, y), (x + w, y + h), (x, y + h) It will be configured. So rect (x, y, w, h) is
quad(x,y, x+w,y, x+w,y+h, x,y+h)
Can be expressed as. Similarly, square (x, y, l) also
rect(x,y,l,l)
And of course this can also be represented by the quad function:
quad(x,y, x+l,y, x+l,y+l, x,y+l)
In this way, in programming, the same expression can be written in various codes. Therefore, the individuality of the author (= programmer) appears in the source code.
To those who don't know programming, programming may seem like a dry task, but it's actually a fairly individual act.
Comp-Position in Color α
If you take a closer look at Mondrian's Composition in Color A, you will see that some of the red rectangles that overlap the blue rectangle have a gap between them and the blue rectangle below. For example:

This is an enlargement of a portion of the figure given at the beginning of this chapter. How should such a picture be realized programmatically?
Now, the only techniques we know are to draw rectangles and straight lines. How can we realize such an expression with only this knowledge?
Do you draw a red square system on the blue square without thinking about it, and then draw it with a white line later?
Or do you divide the blue rectangle below into two rectangles and draw an L-shaped rectangle (that is, draw it as a set of rectangles that do not actually overlap)?
I think there are many possible ways.
In fact, there is no correct answer to this question, and if you get the results you want in any way, that's the correct answer.
Here, I would like to conclude this chapter by introducing how to express a gap by a contour line, taking advantage of the fact that a rectangle drawn by the rect function can also draw a contour line. A program about Composition in Color A will come out later, so this time we named it in Color $ \ alpha $ in the sense of the alpha version.
// comp-position in Color alpha
background(250,245,230);
size(500,500);
strokeWeight(10);
stroke(250,240,240); // same as background
fill(0,80,160); // blue
rect(60,120, 200,150);
fill(220,60,20); // red
rect(230,70, 160,150);
noStroke();
fill(80,80,80); // black
rect(270,230,80,15);
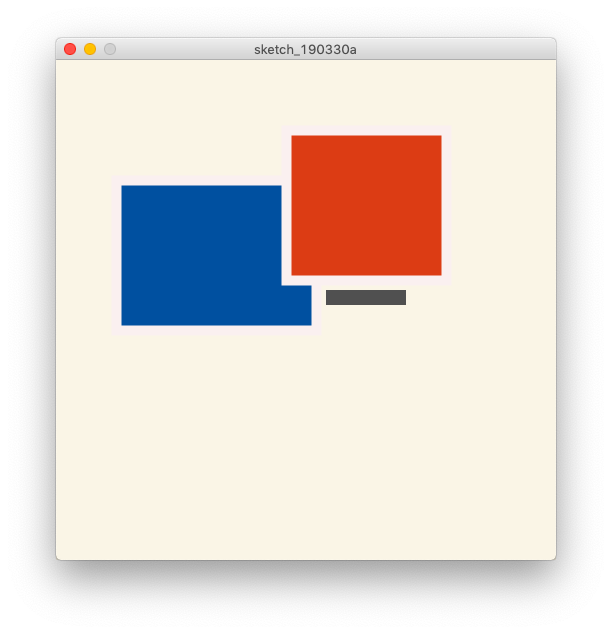
As you can see, there is also a way to not use the contour line as the contour line. Also, when drawing a picture with Processing, Processing has various functions, and it is necessary to be familiar with how to use them and what kind of effects and expressions can be obtained.
Column: α version, β version
In the computer world, we often hear terms such as alpha version and beta version. What the hell is this? The $ \ beta $ version of software (beta version) means that it's almost complete, but there's still some work to be done.
In network games, etc., beta tests are used to actually play with almost completed software to raise bugs, adjust the entire system, and evaluate server performance.
By the way, a product with a degree of perfection that can be a candidate for release (shipment = product version) is called Release Candidate, and abbreviations such as RC are used.
The alpha version means that it is before the beta, and it still needs some work to be almost completed, but it works reasonably well.
The comp-position in Color created above is still lacking compared to Mondrian's Composition in Color A. However, I can still draw something like a picture, so I chose comp-position in Color $ \ alpha $ to mean that it is an alpha version.
Recommended Posts