[JAVA] Einführung in die Programmierung für Studenten: Verschiedene Funktionen in Bezug auf Quadrate (Teil 2)

• Mit Qiita ist es schwierig, nur den Textteil zu drucken. Daher wird derselbe Inhalt auf der folgenden Seite veröffentlicht. Wenn Sie ausdrucken oder in PDF konvertieren möchten, verwenden Sie bitte diese Seite:

http://gurakura.sakura.ne.jp/hellomondrian/rect3/

Klicken Sie hier für eine Liste: http://gurakura.sakura.ne.jp/series/美大生のためのプログラミング入門/

Qiita Version umfassendes Inhaltsverzeichnis: https://qiita.com/iigura/items/37180d127da93d0b8abb

Wie zeichnet man ein unfreies Quadrat?

In diesem Abschnitt wird abschließend erläutert, wie ein nicht freies Viereck im Gegensatz zu einem freien Viereck gezeichnet wird. Ich denke, es gibt verschiedene Definitionen von unbequemen Quadraten, aber hier möchte ich Quadrate als ein Quadrat mit weniger Freiheit aufgreifen, das die gleiche Form (= ähnlich) hat, egal wer es zeichnet.

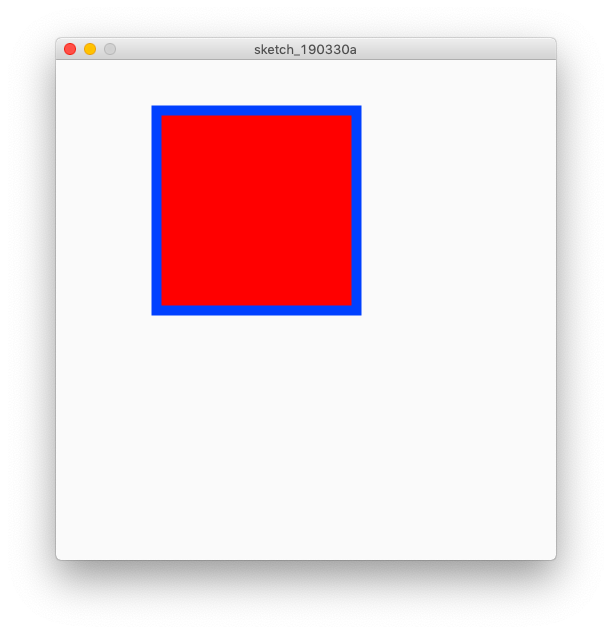
Zeichnen Sie ein Quadrat mit der Quadratfunktion. Das Argument ist quadratisch (x, y, l). x und y sind die oberen linken Positionen des Quadrats und l ist die Länge der Seite.

Anmerkungen: Die mit (x, y) angegebene Referenzposition kann übrigens mit der Funktion rectMode geändert werden.

background(250,250,250);
size(500,500);

strokeWeight(10);
stroke(0,64,255);
fill(255,0,0);
square(100,50,200);

Spalte: Beziehung zwischen Quad, Rect, Square

Sie können die Quad-Funktion verwenden, um die Rect-Funktion darzustellen. Sie können auch die Funktion rect verwenden, um die Quadratfunktion darzustellen. Das durch Rect (x, y, w, h) gezeichnete Viereck hat Eckpunkte (x, y), (x + w, y), (x + w, y + h), (x, y + h). Es wird konfiguriert. Also ist rect (x, y, w, h)

quad(x,y, x+w,y, x+w,y+h, x,y+h)

Kann ausgedrückt werden als. Ebenso Quadrat (x, y, l)

rect(x,y,l,l)

Und das kann natürlich auch durch die Quad-Funktion dargestellt werden:

quad(x,y, x+l,y, x+l,y+l, x,y+l) 

Auf diese Weise können Sie mit der Programmierung denselben Ausdruck in verschiedene Codes schreiben. Daher erscheint die Individualität des Autors (= Programmierers) im Quellcode.

Für diejenigen, die sich mit Programmieren nicht auskennen, mag das Programmieren wie eine trockene Aufgabe erscheinen, aber es ist eigentlich eine ziemlich individuelle Handlung.

Comp-Position in Color α

Wenn Sie sich Mondrians Komposition in Farbe A genauer ansehen, gibt es einige rote Quadrate, die das blaue Quadrat mit einer Lücke zwischen ihnen und dem blauen Quadrat darunter überlappen. Zum Beispiel:

Dies ist eine Vergrößerung eines Teils der Abbildung zu Beginn dieses Kapitels. Wie soll ein solches Bild programmatisch realisiert werden?

Die einzigen Techniken, die wir jetzt kennen, sind das Zeichnen von Quadraten und geraden Linien. Wie können wir einen solchen Ausdruck nur mit diesem Wissen verwirklichen?

Zeichnen Sie ein rotes Quadratsystem auf ein blaues Quadrat, ohne darüber nachzudenken, und zeichnen Sie später eine weiße Linie?

Oder teilen Sie das blaue Viereck unten in zwei Vierecke und zeichnen ein L-förmiges Viereck (dh zeichnen Sie es als eine Reihe von Vierecken, die sich nicht wirklich überlappen)?

Ich denke, es gibt viele Möglichkeiten.

Tatsächlich gibt es keine richtige Antwort auf diese Frage, und wenn Sie in irgendeiner Weise die gewünschten Ergebnisse erzielen, ist dies die richtige Antwort.

Abschließend möchte ich in diesem Kapitel vorstellen, wie die Lücke durch die Konturlinie ausgedrückt wird, indem die Tatsache ausgenutzt wird, dass die Konturlinie auch in dem von der Rect-Funktion gezeichneten Quadrat gezeichnet werden kann. Ein Programm, das auf Komposition in Farbe A basiert, wird später veröffentlicht. Dieses Mal haben wir es in Farbe $ \ alpha $ im Sinne der Alpha-Version benannt.

// comp-position in Color alpha
background(250,245,230);
size(500,500);

strokeWeight(10);
stroke(250,240,240);  // same as background
fill(0,80,160);       // blue
rect(60,120, 200,150);

fill(220,60,20);      // red
rect(230,70, 160,150);

noStroke();
fill(80,80,80);       // black
rect(270,230,80,15);

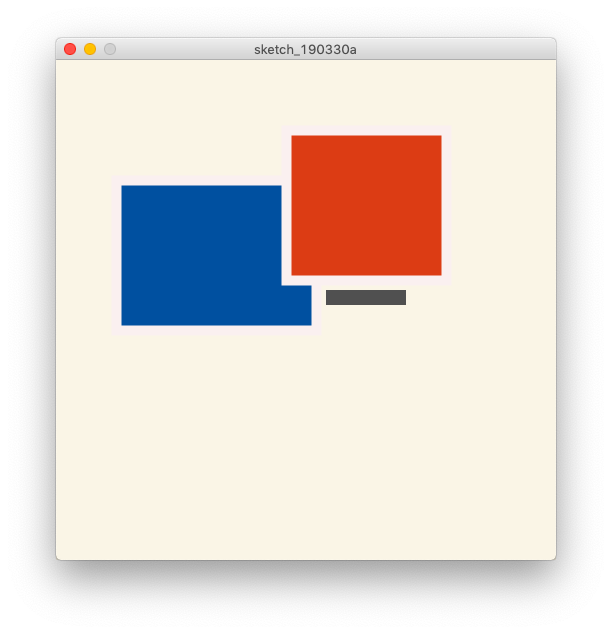
Wie Sie sehen können, gibt es auch eine Möglichkeit, die Konturlinie nicht als Konturlinie zu verwenden. Wenn Sie ein Bild mit Processing zeichnen, müssen Sie außerdem mit den verschiedenen Funktionen von Processing vertraut sein und wissen, wie Sie diese verwenden, um welche Effekte und Ausdrücke zu erhalten.

Spalte: α-Version, β-Version

In der Computerwelt hören wir oft Begriffe wie Alpha und Beta. Was zur Hölle ist das? Die $ \ beta $ -Version (Beta-Version) der Software bedeutet, dass sie fast vollständig ist, aber es gibt noch einige Dinge, die behoben werden müssen.

In Netzwerkspielen usw. werden Betatests durchgeführt, indem tatsächlich mit fast abgeschlossener Software gespielt, Fehler behoben, das gesamte System angepasst und die Serverleistung bewertet werden.

Übrigens wird ein Produkt mit einem Grad an Perfektion, das für eine Freigabe in Frage kommt (Versand = Produktversion), als Freigabekandidat bezeichnet, und es werden Abkürzungen wie RC verwendet.

Die Alpha-Version bedeutet, dass sie vor der Beta-Version liegt und noch fast abgeschlossen sein muss, aber sie funktioniert recht gut.

Die oben erstellte Komposition in Farbe fehlt im Vergleich zu Mondrians Komposition in Farbe A immer noch. Trotzdem kann ich so etwas wie ein Bild zeichnen Ich habe die Kompositionsposition in Farbe $ \ alpha $ gewählt, um zu bedeuten, dass es sich um eine Alpha-Version handelt.