Dieser Artikel ist der 12. Tag von JavaFX Adventskalender 2016. Gestern sind @ skrbs Scene Builder 3 kleine Geschichten. Morgen ist @ sk44_.

Einführung

JavaFX Canvas verfügt über eine 2D-Grafikfunktion, mit der Vektordaten und Bilddaten wie Linien, Rechtecke, Ellipsen und Polygone gezeichnet werden. Sie können auch affine Transformationen angeben, um 2D-Zeichnungen wie Vergrößerung, Verkleinerung, parallele Bewegung, Drehung und Scherung zu transformieren.

Nehmen wir nun an, Sie können die Affin-Konvertierung verwenden, um 2D-Daten anzuzeigen, die größer als der Bildschirm sind, indem Sie sie willkürlich vergrößern oder verkleinern oder nach oben, unten, links oder rechts scrollen, um sie anzuzeigen. Beispiele sind Kartenanzeige und CAD-Datenanzeige.

Das Prinzip der affinen Transformation scheint einfach zu sein, aber es passt oft dazu, wenn ich es versuche, und vor zwei Jahren [Affine Transformation in Canvas passt sehr gut (ich hatte nicht genug mathematischen Sinn ...)]( Ich habe sogar einen Blog namens http://d.hatena.ne.jp/torutk/20140415/p1 geschrieben.

Auf dem JJUG CCC 2016 Herbst am 3. dieses Monats haben wir den Inhalt des Zeichnens von Kartendaten (Weltküstendaten) mit JavaFX Canvas unter dem Titel "Die Welt ist kein Quadrat, das eine Karte mit JavaFX zeichnet" angekündigt. In dem zu diesem Zeitpunkt erstellten Beispielprogramm für die Kartenanzeige wird die Vergrößerung / Verkleinerung / das Scrollen mithilfe der Affin-Konvertierung durchgeführt. Es gab jedoch ein Problem, dass sich die Position der angezeigten Karte beim Vergrößern / Verkleinern verschieben würde. Leider konnte es bis zum Tag der Ankündigung nicht gelöst werden.

Aus Rache habe ich mich daher beim Vergrößern / Verkleinern der Anzeige entschlossen, die Affin-Konvertierung anhand der Grundlagen erneut zu untersuchen und so zu organisieren, dass sich die Mitte der auf dem Bildschirm angezeigten Daten nicht verschiebt.

Ausführungsumgebung dieses Artikels

Dieser Artikel wurde geschrieben, um die affine JavaFX-Konvertierung zu untersuchen und zu verstehen. Daher gibt es kein Beispielprogramm. Um den Betrieb der Affine-Konvertierung einfach zu überprüfen, verwende ich die Befehlszeilenumgebung jshell, die in JDK 9 enthalten sein wird und im nächsten Jahr veröffentlicht wird.

In einer 64-Bit-Umgebung von Windows 10 habe ich Java SE Development Kit 9 Early Access-Version eingefügt und den Shell-Befehl verwendet. Zum Zeitpunkt des Schreibens handelt es sich um die JDK 9 Build 148-Version.

Datenkoordinatensystem und Bildschirmkoordinatensystem

Im Allgemeinen wird die Form von Daten im orthogonalen Koordinatensystem definiert. Dieses orthogonale Koordinatensystem repräsentiert das rechtshändige System, dh die Richtung, in die die positive Richtung der x-Achse als positive Richtung der y-Achse um 90 Grad gegen den Uhrzeigersinn gedreht wird.

Andererseits werden JavaFX-Bildschirmkoordinaten auch im orthogonalen Koordinatensystem definiert, das das linkshändige System darstellt, dh die Richtung, in die die positive Richtung der x-Achse um 90 Grad im Uhrzeigersinn als positive Richtung der y-Achse gedreht wird. ..

データ座標系と画面座標系.png

Wenn die Datenkoordinaten so wie sie sind auf dem Bildschirm angezeigt werden, stehen sie daher auf dem Kopf.

Bei der Anzeige von Kartendaten ohne Konvertierung ...

Kartendaten werden im Allgemeinen in Breiten- und Längengradkoordinaten definiert. Wenn man dies auf der y-Achse für den Breitengrad und der x-Achse für den Längengrad ausdrückt, sind die Daten wie folgt.

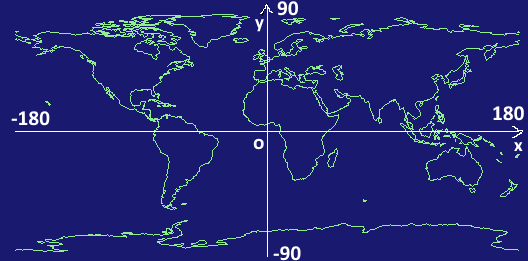
Wenn diese Kartendaten ohne Koordinatenkonvertierung auf dem Bildschirm angezeigt werden, sieht die Anzeige wie folgt aus.

Der Bereich vom ersten Quadranten (0,0) bis (180,90) des Koordinatensystems der Kartendaten wird verkehrt herum angezeigt.

Daher werden wir eine Koordinatenkonvertierung vom Datenkoordinatensystem zum Bildschirmkoordinatensystem einführen, damit die Daten durch willkürliches Vergrößern / Verkleinern / paralleles Bewegen / Drehen angezeigt werden können. Die zu diesem Zeitpunkt verwendete Koordinatentransformation ist die affine Transformation.

Konvertierung vom Datenkoordinatensystem zum Bildschirmkoordinatensystem durch Affin-Konvertierung

Das Datenkoordinatensystem sei das xy-Koordinatensystem und das Bildschirmkoordinatensystem das x'y'-Koordinatensystem. Unter der Annahme, dass die Punkte auf dem xy-Koordinatensystem (x, y) und die Punkte auf dem x'y'-Koordinatensystem (x ', y') sind, ist die Koordinatenkonvertierung vom Datenkoordinatensystem zum Bildschirmkoordinatensystem (x, y). ) Ist die Eingabe und (x ', y') ist die Ausgabe.

x' = ax + by + t_x\\
y' = cx + dy + t_y

Wenn diese Umrechnungsformel als Vektor für Koordinaten und als Matrix für die Umrechnung erneut ausgedrückt wird,

\begin{pmatrix}
x'\\ 
y'\\
1
\end{pmatrix}
= \begin{pmatrix}
a & b & t_x\\
c & d & t_y\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
1
\end{pmatrix}

Es wird sein. Diese Matrix wird zur affinen Transformationsmatrix. (Bei 2 Dimensionen) In Bezug auf die Handhabung der Berechnung wird sie mit einem kubischen Vektor / einer kubischen Matrix (Koordinaten gleicher Ordnung) berechnet.

Koordinatentransformation (1): Einheitliche Transformation

x' = x\\
y' = y\\

Wenn Sie die Konvertierung anwenden (dh nichts konvertieren), wird die Anzeige auf dem Kopf stehen. Durch affine Umwandlung ausgedrückt, ist es wie folgt.

\begin{pmatrix}
x'\\y\\1'
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\y\\1
\end{pmatrix}

Bei dieser Konvertierung (keine Konvertierung) werden die Daten wie folgt auf dem Bildschirm angezeigt.

データ座標→画面座標（恒等変換）.png

Der gelbe rechteckige Teil ist der Bildschirmzeichnungsbereich. Die Punkte A, B und C werden wie folgt in A ', B' umgewandelt (keine Umwandlung).

\begin{align*}
(A'_x, A'_y) &= (A_x, A_y) = (160, 200)\\
(B'_x, B'_y) &= (B_x, B_y) = (320, 0)\\
(C'_x, C'_y) &= (C_x, C_y) = (160, -200)
\end{align*}

Diese affine Transformation wird mit dem folgenden Code erstellt.

Affine affine = new Affine();

Experimentieren mit Affine in der jshell-Umgebung von JDK 9

Fügen Sie die Umgebungsvariable PATH in JDK 9 ein. Führen Sie jshell aus.

C:\>java -version
java version "9-ea"
Java(TM) SE Runtime Environment (build 9-ea+148)
Java HotSpot(TM) 64-Bit Server VM (build 9-ea+148, mixed mode)

C:\>jshell
|Willkommen bei JShell--Version 9-ea
|Geben Sie für eine Übersicht Folgendes ein: /help intro
|
jshell>

Erzeugt eine affine Transformation (gleiche Transformation).

jshell> import javafx.scene.transform.Affine

jshell> Affine affine = new Affine()
affine ==> Affine [
        1.0, 0.0, 0.0, 0.0
        0.0, 1.0, 0.0, 0.0
        0.0, 0.0, 1.0, 0.0
]

Die jshell-Umgebung ist praktisch, da sie den Inhalt der definierten Variablen anzeigt. Es wird jedoch in 3 Zeilen und 4 Spalten angezeigt. Dies liegt daran, dass JavaFX standardmäßig mit 3D-Grafiken geliefert wird, sodass 3D-Koordinatentransformationen verarbeitet werden können.

Machen Sie sich beim Umgang mit affinen 2D-Transformationen keine Gedanken über die dritte Spalte, wie oben gezeigt.

Als nächstes erstellen wir einen Punkt im Datenkoordinatensystem und konvertieren ihn mit dieser Affine.

jshell> import javafx.geometry.Point2D

jshell> Point2D dataA = new Point2D(160, 200)
dataA ==> Point2D [x = 160.0, y = 200.0]

jshell> affine.transform(dataA)
$5 ==> Point2D [x = 160.0, y = 200.0]

jshell>

Als Ergebnis dieser affinen Umwandlung wurden Koordinaten mit den gleichen Werten wie die ursprünglichen Koordinaten (160.200) erhalten.

Koordinatenumrechnung (2): Beseitigung von verkehrt herum

Da die y-Achse umgekehrt ist, denken wir, dass wir einfach das Vorzeichen der y-Koordinate umkehren und die folgende Koordinatentransformation einführen können.

\begin{align*}
x' &= x\\
y' &= -y\\
\end{align*}

Durch affine Umwandlung ausgedrückt, ist es wie folgt.

\begin{pmatrix}
x'\\y'\\1
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & 0\\
0 & -1 & 0\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\y\\1
\end{pmatrix}

データ座標→画面座標（上下反転）.png

Die Punkte A, B und C werden in A ', B' umgewandelt, wie folgt.

\begin{align*}
(A'_x, A'_y) &= (A_x, -A_y) = (160, -200)\\
(B'_x, B'_y) &= (B_x, -B_y) = (320, 0)\\
(C'_x, C'_y) &= (C_x, -C_y) = (160, 200)
\end{align*}

Die Datenanzeige wurde verkehrt herum aufgelöst, aber der Datenanzeigebereich ist nicht mit dem Anzeigebereich in (Teil 1) (gegenüber der X-Achse) ausgerichtet.

Diese affine Transformation wird mit dem folgenden Code erstellt.

Affine affine = new Affine(1, 0, 0, 0, -1, 0);

Experimentieren mit Affine in der jshell-Umgebung von JDK 9

jshell> affine = new Affine(1, 0, 0, 0, -1, 0)
affine ==> Affine [
        1.0, 0.0, 0.0, 0.0
        0.0, -1.0, 0.0, 0.0
        0.0, 0.0, 1.0, 0.0
]

jshell> affine.transform(dataA)
$9 ==> Point2D [x = 160.0, y = -200.0]

jshell>

Punkt A wurde von (160, 200) in (160, -200) konvertiert. In ähnlicher Weise sehen wir uns die Umrechnungsergebnisse für die Punkte B und C an.

jshell> Point2D dataB = new Point2D(320, 0)
dataB ==> Point2D [x = 320.0, y = 0.0]

jshell> affine.transform(dataB)
$12 ==> Point2D [x = 320.0, y = -0.0]

jshell> Point2D dataC = new Point2D(160, -200)
dataC ==> Point2D [x = 160.0, y = -200.0]

jshell> affine.transform(dataC)
$13 ==> Point2D [x = 160.0, y = 200.0]

jshell>

Punkt B wurde von (320, 0) nach (320, -0) konvertiert (Koordinatenwerte ändern sich nicht). Punkt C wurde von (160, -200) in (160, 200) konvertiert.

Koordinatenumrechnung (3): Parallele Ursprungsbewegung

Der Ursprung des Datenkoordinatensystems ist die untere linke Ecke des Bereichs, den Sie zeichnen möchten, aber der Ursprung des Bildschirmkoordinatensystems ist die obere linke Ecke des zu zeichnenden Bereichs. Verschieben Sie daher den Ursprung des Datenkoordinatensystems parallel zum Ursprung des Bildschirmkoordinatensystems, um ihn an den Bereich anzupassen, den Sie zeichnen möchten.

In diesem Fall ist die parallele Bewegung die Höhe des Zeichenbereichs in Richtung der y-Achse. Wenn die Höhe des Zeichenbereichs h ist, lautet die Umrechnungsformel wie folgt.

\begin{align*}
x' &= x\\
y' &= -(y - h) = -y + h\\
\end{align*}

Durch affine Umwandlung ausgedrückt, ist es wie folgt.

\begin{pmatrix}
x'\\y'\\1
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & 0\\
0 & -1 & h\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\y\\1
\end{pmatrix}

Die Figur und jede Koordinate bei einer Höhe h von 200 sind wie folgt.

データ座標→画面座標（上下反転＋原点一致）.png

\begin{align*}
(A'_x, A'_y) &= (A_x, -A_y + 200) = (160, 0)\\
(B'_x, B'_y) &= (B_x, -B_y + 200) = (320, 200)\\
(C'_x, C'_y) &= (C_x, -C_y + 200) = (160, 0)
\end{align*}

Diese affine Transformation wird mit dem folgenden Code erstellt.

Affine affine = new Affine(1, 0, 0, 0, -1, 200);

Experimentieren mit Affine in der jshell-Umgebung von JDK 9

jshell> affine = new Affine(1, 0, 0, 0, -1, 200)
affine ==> Affine [
        1.0, 0.0, 0.0, 0.0
        0.0, -1.0, 0.0, 200.0
        0.0, 0.0, 1.0, 0.0
]

jshell> affine.transform(dataA)
$19 ==> Point2D [x = 160.0, y = 0.0]

jshell> affine.transform(dataB)
$20 ==> Point2D [x = 320.0, y = 200.0]

jshell> affine.transform(dataC)
$21 ==> Point2D [x = 160.0, y = 400.0]

jshell>

Punkt A wurde von (160, 200) nach (160, 0) konvertiert. Punkt B wurde von (320, 0) in (320, 200) konvertiert. Punkt C wurde von (160, -200) in (160, 400) konvertiert.

Koordinatenkonvertierung (4): Verschieben Sie den Zeichenbereich

Verschieben Sie den Zeichenbereich in einen beliebigen Teil des Datenkoordinatensystems. Unter der Annahme, dass die Koordinaten der oberen linken Ecke des Zeichenbereichs (x1, y1) sind, drückt die folgende Formel die parallele Bewegung aus.

\begin{align*}
x' &= x - x_1\\
y' &= -(y - y_1) = -y + y_1
\end{align*}

Durch affine Umwandlung ausgedrückt, ist es wie folgt.

\begin{pmatrix}
x'\\y'\\1
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & -x_1\\
0 & -1 & y_1\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\y\\1
\end{pmatrix}

Die Figur und jede Koordinate, wenn (x1, y1) (-280, 500) ist, sind wie folgt.

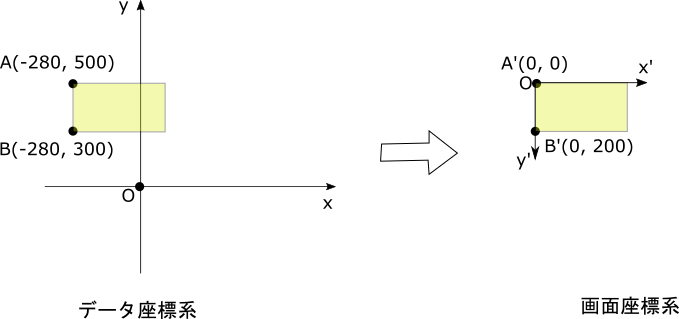
データ座標→画面座標（平行移動）.png

\begin{align*}
(A'_x, A'_y) &= (A_x - (-280), -(A_y - 500))\\
 &= (A_x + 280, -A_y + 500)\\
 &= (0, 0)\\
(B'_x, B'_y) &= (B_x - (-280), -(B_y - 500))\\
 &= (B_x + 280, -B_y + 500)\\
 &= (0, 200)
\end{align*}

Diese affine Transformation wird mit dem folgenden Code erstellt.

Affine affine = new Affine(1, 0, 280, 0, -1, 500);

Es ist ein bisschen verwirrend.

Betrachten Sie eine Kombination aus zwei Koordinatentransformationen.

Parallele Bewegung
Umgedreht

Die parallele bewegungsaffine Transformation wird durch die folgende Matrixgleichung ausgedrückt.

\begin{pmatrix}
1 & 0 & -x_1\\
0 & 1 & -y_1\\
0 & 0 & 1
\end{pmatrix}

Die auf dem Kopf stehende affine Transformation wird durch die folgende Matrixgleichung ausgedrückt.

\begin{pmatrix}
1 & 0 & 0\\
0 & -1 & 0\\
0 & 0 & 1
\end{pmatrix}

Führen Sie zuerst eine parallele Bewegung durch und drehen Sie sie dann um. In diesem Fall schreiben Sie beim Verbinden einer Matrix die zuerst anzuwendende auf die rechte Seite.

\begin{pmatrix}
1 & 0 & 0\\
0 & -1 & 0\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & -x_1\\
0 & 1 & -y_1\\
0 & 0 & 1
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & -x_1\\
0 & -1 & y_1\\
0 & 0 & 1
\end{pmatrix}

Experimentieren mit Affine in der jshell-Umgebung von JDK 9

Kombiniere zwei Affinen.

jshell> Affine affineMove = new Affine(1, 0, -(-280), 0, 1, -500)
affineMove ==> Affine [
        1.0, 0.0, 0.0, 280.0
        0.0, 1.0, 0.0, -500.0
        0.0, 0.0, 1.0, 0.0
]

jshell> Affine affineReverse = new Affine(1, 0, 0, 0, -1, 0)
affineReverse ==> Affine [
        1.0, 0.0, 0.0, 0.0
        0.0, -1.0, 0.0, 0.0
        0.0, 0.0, 1.0, 0.0
]

jshell> affineReverse.createConcatenation(affineMove)
$35 ==> Affine [
        1.0, 0.0, 0.0, 280.0
        0.0, -1.0, 0.0, 500.0
        0.0, 0.0, 1.0, 0.0
]

Nun, es ist immer noch schwer zu verstehen ...

Lassen Sie uns nun die Koordinatenkonvertierung durchführen.

jshell> affine = new Affine(1, 0, 280, 0, -1, 500)
affine ==> Affine [
        1.0, 0.0, 0.0, 280.0
        0.0, -1.0, 0.0, 500.0
        0.0, 0.0, 1.0, 0.0
]

jshell> Point2D dataJ = new Point2D(-280, 500)
dataJ ==> Point2D [x = -280.0, y = 500.0]

jshell> affine.transform(dataJ)
$29 ==> Point2D [x = 0.0, y = 0.0]

jshell> Point2D dataK = new Point2D(-280, 300)
dataK ==> Point2D [x = -280.0, y = 300.0]

jshell> affine.transform(dataK)
$30 ==> Point2D [x = 0.0, y = 200.0]

Das Datenkoordinatensystem (-280, 500) wurde in das Bildschirmkoordinatensystem (0, 0) konvertiert. Das Datenkoordinatensystem (-280, 300) wurde in das Bildschirmkoordinatensystem (0, 200) konvertiert.

Koordinatenumwandlung (5): Skalierung und parallele Bewegung

Vergrößert oder verkleinert den Zeichenbereich des Datenkoordinatensystems auf eine beliebige Größe. Unter der Annahme, dass das Vergrößerungsverhältnis S ist und die Koordinaten der oberen linken Ecke des Zeichenbereichs im Datenkoordinatensystem (x1, y1) sind, drückt die folgende Gleichung Vergrößerung / Verkleinerung und parallele Bewegung aus.

\begin{align*}
x' &= s(x - x_1) = sx - sx_1\\
y' &= -s(y - y_1) = -sy + sy_1
\end{align*}

Durch Affin-Konvertierung ausgedrückt, ist es wie folgt.

\begin{pmatrix}
x'\\y'\\1
\end{pmatrix}=
\begin{pmatrix}
s & 0 & -sx_1\\
0 & -s & sy_1\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\y\\1
\end{pmatrix}

Bei Vergrößerung 2 und Parallelbewegung (0, 100)

Schauen wir uns hier den Anzeigebereich des Datenkoordinatensystems und die Konvertierung in das Bildschirmkoordinatensystem an, wenn das Vergrößerungsverhältnis 2 und der Betrag der parallelen Bewegung (0,100) beträgt.

データ座標→画面座標（スケール１）.png

Da die Vergrößerung verdoppelt wird, wird der Bereich von 160 × 100 im Datenkoordinatensystem im Bildschirmkoordinatensystem 320 × 200 gezeichnet.

\begin{align*}
(A'_x, A'_y) &= (2A_x +2.0, -2A_y +2.100)\\
 &= (0, 0)\\
(B'_x, B'_y) &= (2B_x +2.0, -2B_y +2.100)\\
 &= (320, 0)\\
(C'_x, C'_y) &= (2C_x +2.0, -2C_y +2.100)\\
 &= (320, 200)
\end{align*}

Der Inhalt der Daten sieht wie in der folgenden Abbildung aus.

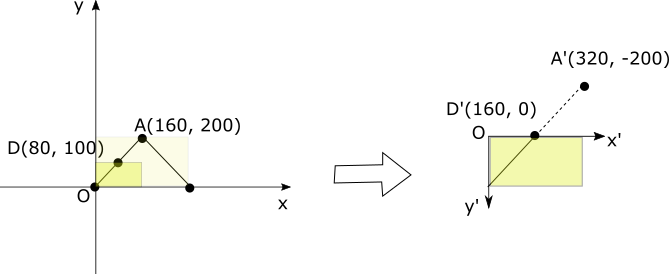
データ座標→画面座標（スケール）.png

Diese affine Transformation wird mit dem folgenden Code erstellt.

Affine affine = new Affine(2, 0, 0, 0, -2, 200);

Experimentieren mit Affine in der jshell-Umgebung von JDK 9

jshell> affine = new Affine(2, 0, 0, 0, -2, 200)
affine ==> Affine [
        2.0, 0.0, 0.0, 0.0
        0.0, -2.0, 0.0, 200.0
        0.0, 0.0, 1.0, 0.0
]

jshell> dataA = new Point2D(0, 100)
dataA ==> Point2D [x = 0.0, y = 100.0]

jshell> affine.transform(dataA)
$38 ==> Point2D [x = 0.0, y = 0.0]

jshell> dataB = new Point2D(160, 100)
dataB ==> Point2D [x = 160.0, y = 100.0]

jshell> affine.transform(dataB)
$40 ==> Point2D [x = 320.0, y = 0.0]

jshell> dataC = new Point2D(160, 0)
dataC ==> Point2D [x = 160.0, y = 0.0]

jshell> affine.transform(dataC)
$42 ==> Point2D [x = 320.0, y = 200.0]

Das Datenkoordinatensystem (0, 100) wurde in das Bildschirmkoordinatensystem (0, 0) konvertiert. Das Datenkoordinatensystem (160, 100) wurde in das Bildschirmkoordinatensystem (320, 0) konvertiert. Das Datenkoordinatensystem (160, 0) wurde in das Bildschirmkoordinatensystem (320, 200) konvertiert.

Beispiel mit 0,5-facher Vergrößerung und paralleler Bewegung (100, 1000)

Die Umrechnungszahl, wenn die Vergrößerung 0,5 beträgt und der Betrag der parallelen Bewegung (100.1000) beträgt, ist unten gezeigt.

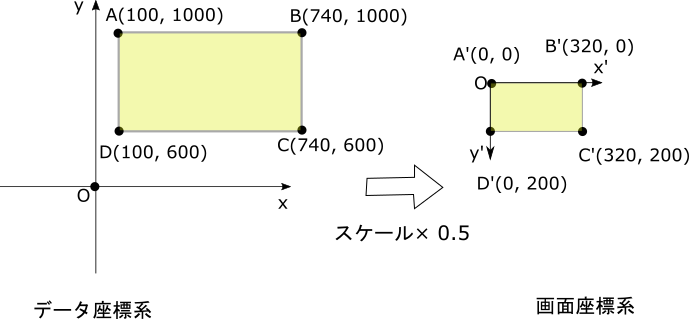
データ座標→画面座標（スケール＋平行移動）.png

Die affine Transformationsmatrix ist zu diesem Zeitpunkt wie folgt.

\begin{pmatrix}
0.5 & 0 & -50\\
0 & -0.5 & 500\\
0 & 0 & 1
\end{pmatrix}

Experimentieren mit Affine in der jshell-Umgebung von JDK 9

jshell> Affine affine = new Affine(0.5, 0, -50, 0, -0.5, 500)
affine ==> Affine [
        0.5, 0.0, 0.0, -50.0
        0.0, -0.5, 0.0, 500.0
        0.0, 0.0, 1.0, 0.0
]

jshell> affine.transform(100, 1000)
$4 ==> Point2D [x = 0.0, y = 0.0]

jshell> affine.transform(740, 1000)
$5 ==> Point2D [x = 320.0, y = 0.0]

jshell> affine.transform(740, 600)
$6 ==> Point2D [x = 320.0, y = 200.0]

jshell> affine.transform(100, 600)
$7 ==> Point2D [x = 0.0, y = 200.0]

jshell>

Dieses Mal habe ich versucht, den x-Koordinatenwert und den y-Koordinatenwert anstelle der Point2D-Instanz direkt als Eingabe für die Konvertierung einzugeben.

Das Datenkoordinatensystem (100, 1000) wurde in das Bildschirmkoordinatensystem (0, 0) konvertiert. Das Datenkoordinatensystem (740, 1000) wurde in das Bildschirmkoordinatensystem (320, 0) konvertiert. Das Datenkoordinatensystem (740, 600) wurde in das Bildschirmkoordinatensystem (320, 200) konvertiert. Das Datenkoordinatensystem (100, 600) wurde in das Bildschirmkoordinatensystem (0, 200) konvertiert.

Koordinatenumrechnung (6): Vergrößerung / Verkleinerung in der Mitte des Bildschirms

Bei der bisherigen Vergrößerung / Verkleinerung der Koordinatenkonvertierung wird oben links auf dem Bildschirm als Basispunkt verwendet. Schauen wir uns als nächstes die Anzeige eines Canvas-Beispielprogramms an, das die bisherige Koordinatentransformation implementiert. Wenn Sie von Anzeige (1) zu Anzeige (3) erweitern, können Sie sehen, dass die Anzeige auf der oberen linken Ecke basiert.

Anzeige (1)
Anzeige (2)
Anzeige (3)

Als intuitive Bedienung möchte ich Sie jedoch bitten, mit der Mitte des Bildschirms als Basispunkt hinein- und herauszuzoomen.

Daher werden wir dieses Mal eine parallele Bewegung hinzufügen, die die Koordinaten der oberen linken Ecke des Bildschirms in die Mitte des Bildschirms im Bildschirmkoordinatensystem verschiebt.

Zunächst wird die in "Koordinatentransformation (5): Vergrößerung / Verkleinerung und Parallelbewegung" verwendete Formel für die Koordinatentransformation erneut aufgeführt.

\begin{align*}
x' &= sx - sx_1 \\
y' &= -sy + sy_1
\end{align*}

Sei w die Breite des Bildschirms und h die Höhe des Bildschirms. Die Koordinatenumrechnungsformel für den Vorgang des Verschiebens der oberen linken Ecke des Bildschirms parallel zur Mitte des Bildschirms lautet wie folgt.

\begin{align*}
x'' &= x' + \frac{w}{2}\\
y'' &= y' + \frac{h}{2}
\end{align*}

Die Koordinatenkonvertierungsformel, mit der die Operation zum Verschieben der oberen linken Ecke des Bildschirms parallel zur Mitte des Bildschirms hinzugefügt wird, lautet wie folgt.

\begin{align*}
x'' &= sx - sx_1 + \frac{w}{2}\\
y'' &= -sy + sy_1 + \frac{h}{2}
\end{align*}

Da die parallele Bewegung gemäß der Bildschirmgröße nicht durch die Skalierung des Datenkoordinatensystems beeinflusst wird, wird der Skalierungsfaktor s nicht wie in der obigen Formel angewendet.

Die Abbildung ist unten dargestellt.

データ座標→画面座標（画面中心）.png

Die affine Transformation wird durch den folgenden Matrixausdruck ausgedrückt.

\begin{pmatrix}
s & 0 & -sx_1 + \frac{w}{2}\\
0 & -s & sy_1 + \frac{h}{2}\\
0 & 0 & 1
\end{pmatrix}

Experimentieren mit Affine in der jshell-Umgebung von JDK 9

Wenn die Bildschirmgröße 320 x 200 beträgt, beträgt die Koordinate der oberen linken Ecke des Zeichenbereichs im Datenkoordinatensystem (200, 500) und der Maßstab 2.

jshell> affine = new Affine(2, 0, -240, 0, -2, 1100)
affine ==> Affine [
        2.0, 0.0, 0.0, -240.0
        0.0, -2.0, 0.0, 1100.0
        0.0, 0.0, 1.0, 0.0
]

jshell> affine.transform(200, 500)
$12 ==> Point2D [x = 160.0, y = 100.0]

Sie können sehen, dass die obere linke Ecke (200, 500) des Datenkoordinatensystems im Bildschirmkoordinatensystem und in der Bildschirmmitte in (160, 100) konvertiert wurde.

Wenn die Bildschirmgröße 320 x 200 beträgt, beträgt die Koordinate der oberen linken Ecke des Zeichenbereichs im Datenkoordinatensystem (200, 500) und der Maßstab 0,5.

jshell> affine = new Affine(0.5, 0, 60, 0, -0.5, 350)
affine ==> Affine [
        0.5, 0.0, 0.0, 60.0
        0.0, -0.5, 0.0, 350.0
        0.0, 0.0, 1.0, 0.0
]

jshell> affine.transform(200, 500)
$14 ==> Point2D [x = 160.0, y = 100.0]

Sie können sehen, dass die obere linke Ecke (200, 500) des Datenkoordinatensystems im Bildschirmkoordinatensystem und in der Bildschirmmitte in (160, 100) konvertiert wurde.

Zusammenfassung

Die affinen Transformationen, die zum Anzeigen der im rechtshändigen orthogonalen Koordinatensystem definierten Daten auf dem Bildschirm verwendet werden, lauten wie folgt:

\begin{pmatrix}
s & 0 & -sx_1 + \frac{w}{2}\\
0 & -s & sy_1 + \frac{h}{2}\\
0 & 0 & 1
\end{pmatrix}

Jedoch,\\
s ist die Expansionsrate\\
(x_1, y_1)Sollen die Datenkoordinaten in der Mitte des Bildschirms angezeigt werden?\\
(w, h)Ist die Breite und Höhe der Anzeigegröße im Bildschirmkoordinatensystem

Referenz / verwandte Informationen

Das Beispielprogramm für die Bildschirmanzeige auf JavaFX Canvas, das diese affine Konvertierung verwendet, und seine Erklärung werden unten beschrieben.

[Operation zum Zeichnen und Skalieren von Vektoren mit JavaFX Canvas](http://www.torutk.com/projects/swe/wiki/JavaFX_Canvas%E3%82%92%E4%BD%BF%E3%81% A3% E3% 81% 9F% E3% 83% 99% E3% 82% AF% E3% 82% BF% E3% 83% BC% E6% 8F% 8F% E7% 94% BB% E3% 81% A8% E6% 8B% A1% E5% A4% A7% E7% B8% AE% E5% B0% 8F% E7% A7% BB% E5% 8B% 95% E6% 93% 8D% E4% BD% 9C)

Die auf der JJUG CCC 2016 Herbst vorgestellten Folien, die mich zum Schreiben dieses Artikels inspiriert haben, lauten wie folgt.

Ein Blog, der schrieb, dass ich in der Vergangenheit an der Affin-Konvertierung mit Canvas beteiligt war

Affine Konvertierung mit Canvas passt sehr gut (ich hatte nicht genug mathematischen Sinn ...)

Vergrößern / verkleinern und parallel zu JavaFX Canvas verschieben (Revenge Edition)

Einführung

Ausführungsumgebung dieses Artikels

Datenkoordinatensystem und Bildschirmkoordinatensystem

Bei der Anzeige von Kartendaten ohne Konvertierung ...

Konvertierung vom Datenkoordinatensystem zum Bildschirmkoordinatensystem durch Affin-Konvertierung

Koordinatentransformation (1): Einheitliche Transformation

Experimentieren mit Affine in der jshell-Umgebung von JDK 9

Koordinatenumrechnung (2): Beseitigung von verkehrt herum

Experimentieren mit Affine in der jshell-Umgebung von JDK 9

Koordinatenumrechnung (3): Parallele Ursprungsbewegung

Experimentieren mit Affine in der jshell-Umgebung von JDK 9

Koordinatenkonvertierung (4): Verschieben Sie den Zeichenbereich

Experimentieren mit Affine in der jshell-Umgebung von JDK 9

Koordinatenumwandlung (5): Skalierung und parallele Bewegung

Bei Vergrößerung 2 und Parallelbewegung (0, 100)

Beispiel mit 0,5-facher Vergrößerung und paralleler Bewegung (100, 1000)

Koordinatenumrechnung (6): Vergrößerung / Verkleinerung in der Mitte des Bildschirms

Experimentieren mit Affine in der jshell-Umgebung von JDK 9

Zusammenfassung

Referenz / verwandte Informationen