(complex) It depends on how to name the coefficient of the morlet wavelet, the appropriate setting value, and the material, so I tried to organize it as much as possible.
I can't organize it very much, but ...
1. I'm not sure if the variables and expressions in the wavelet expression are slightly different and point to the exact same thing.
ref. From Matlab's material (probably) Teolis (1998) Computational Signal Proceesing with Wavelets. P66
formula
Variable name
γb: named variance (bandwidth). Same as fb in matlab material. It seems to be temporal variance. But what is temporal variance here? It's named γc: center frequency. It's almost the same. I understand that it's a value to set with mne or frequencies = np.arange (8,30). j: Imaginary unit
ref. stack overflow
formula
w (t, f 0 </ sub>) = A ・ exp (−t 2 </ sup> / 2 * σ 2 </ sup>) ・ exp (2 * i * π * f 0 </ sub> * t) = A ・ exp (2 iπ f 0 </ sub> t-(t 2 </ sup> / 2σ 2 </ sup> >))
variable
f 0 </ sub>: center frequency (γc above, fc in matlab wavelet toolbox) It is described as σ: σ = m / 2πf 0 </ sub>. As described in [Tallon-Baudry (1999)] 3, the meaning of the standard deviation (sigmat) with respect to time. Compared to the Teolis (1998) equation above, It matches assuming that γb = 2σ 2 </ sup>. m: constant. Compromise between time and frequency resolution. I set it to 7. A = 1 / (σ (2π) 0.5 </ sup>) = 1 / (σ√2π): The part before e (exp) is replaced with a variable. Introduced under the name normalization factor Yes.
ref. [Tallon-Baudry (1999)] 3, p154 Box 2 Description
formula
w (t, f) = A. exp (– t 2 </ sup> / 2σ t </ sub> 2 </ sup>). exp (2i π ft): This is Same as stack overflow.
variable
f: Same as f 0 </ sub> above. Center frequency σ t </ sub>: Same as σ above. Described as standard deviation of time domain.
** A = 1 / (σt √π) 1/2 **: It is written as normalization factor like [stack overflow] 2. The formula is a little different. [Tallon-Baudry (1997)] 11 It has the same description. It is unknown whether it is intentional or wrong + copy.
formula
ψ (x) = 1 / √πfb * ** exp (x 2 </ sup> / fb) ** * exp (2iπfcx): Copy and paste did not work, so copy it. Compared to the above two, ** exp (x 2 </ sup> / fb) ** has no ** minus **. This page is the only one, so I feel like I made a mistake. .. Others match Teolis (1998), stack overflow
variable
x: Same as t above fc: Same as f0, f, γc above. Center frequency fb: named bandwidth parameter. Same as γb in Teolis (1998).
ref. matlab help
formula
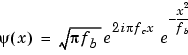It's also a little different. The denominator and numerator are reversed in the part before e (A: normalization factor that appears above). The difference between the denominator and numerator is only this page, so it's probably wrong.
Others match Teolis (1998), stack overflow
variable
The naming of fc and fb is the same as [matlab wavelet toolbox] 4
ref. [Stack exchange] 7 wavelet cmor fb fc or something like that will hit the top.
formula
The minus of e -j2pifct </ sup> seems unnecessary.
Summary of 1
Comprehensive judgment (complex) Morlet wavelt's formula is Teolis (1998) Computational Signal Proceesing with Wavelets. P66, Stack overflow seems to be correct. Teolis (1998) is a text. The formula is really slightly different depending on the material, and I feel that it is actually full of mistakes.
2. What is a good wavelet setting? (Mainly with mne python in mind)
[fieldtrip] 9(time-frequency analysis, wavelet section)
cfg.width. It determines the ** width ** of the wavelets in number of cycles. In the sample
cfg.width = 7;
It was. Also, The spectral bandwidth at a given frequency F is equal to F/width*2 the wavelet duration is equal to width/F/pi F is the frequency, which seems to be the same as the center frequency (f, f 0 </ sub>, γc, fc) above.
--I just don't know what spectral bandwidth and wavelet duration mean. --It seems that it is not such a simple relationship that the spectral bandwidth matches σ f </ sub> and the wavelet duration matches σ t </ sub>. There are many terms and it is confusing.
Tallon-Baudry(1999) ** σ f </ sub> = 1 / (2πσ t </ sub>) ** (Equation 2.1) The relationship is shown.
--σ t </ sub> is described as standard deviation (time domain). It seems to be the same as σ t </ sub> and σ that have appeared several times. --σ f </ sub> is also described as standard deviation (frequency domain).
** f / σ f </ sub> (constant ratio: greater than five in practice) ** (Equation 2.2).
--f seems to be the same as center frequency (F in the field trip, f 0 </ sub>, γc, fc that appears above).
Roach & Mathalon (2008) ** σ t </ sub> = 1 / (2πσ f </ sub>) ** (Equation 2.3) It is the same if the equation (2.1) of [Tallon-Baudry (1999)] 3 is transformed.
Description of variables
σ t </ sub>: Described as temporal SD. σ f </ sub>: spectral bandwidth around its center frequency, f0, that has a SD of σ f </ sub>, so it can be said that it is SD of frequency. Morlet wavelet is gaussian envelope ( Since the word (normally distributed envelope) appears frequently, SD may be easy to use as an index in the form of a wavelet. Just at the bottom of the same page spectral bandwidth around any given center frequency is mσf. There is also a. m is multiplied. To infer from these spectral bandwith = mσf , and has σf in it. I imagine that it means. I am troubled with the description that confuses the text.
** c = f 0 </ sub> / σ f </ sub> ** (Equation 2.4) And ** c (constant ratio) ** are defined ** (probably the same thing as cfg.width) **. This also points to the same thing, just the variable c is assigned to Equation 2.2. It is thought that there is.
--It is recommended in the text that c should be a number around 5,6,7, so that σ t </ sub> contains waves with one or more cycles ("constan"). , c, is typically recommended to be greater than 5, and is often set to values of 6 or 7, which corresponds to a σ t </ sub> that thereby at least one full sinusoidal cycle for any particular frequency ") .- -In [stack overflow] 2, the formula ** σ = m / (2 π f 0 </ sub>) ** appears, and (σ = σ t </ sub> (Maybe), which matches equation (2.5) below, so it seems that m and constant ratio c in this equation point to the same thing.
A little digression: Explanation that σ t </ sub> contains waves with one or more cycles when c is about 7 (may be wrong)
When transformed into the form of σ t </ sub> = using equations (2.3) and (2.4)
** σ t </ sub> = c / (2πf) = c / (2π) * 1 / f ** (Equation 2.5) is obtained.
--Since f is the frequency, 1 / f is the time for one cycle. --So, if c / (2π) before 1 / f exceeds 1, σ t </ sub> will contain waves of one or more cycles (why such a length I don't know why you need it) but you can meet the recommendations. ―― 2π = 6.28 Since it is a little, it is considered that c / (2π)> 1 at c = 7 and σ t </ sub> includes waves exceeding one period.
** Variable m I don't understand **
[Roach & Mathalon (2008)] 10 explains it as a factor m. ** temporary window for any given frequency (f 0 </ sub>) is m σ t </ sub> ** (Equation 2.6) I'm not sure what the temporal window points to. However, I feel that the temporal window is the same as the wavelet duration that appears in [field trip] 9. Let's transform the expression.
From equations (2.6) and (2.5) temporal window = mc / (2π) * 1 / f = mc / (2π) / f. I repeat the description in the field trip section above,
** wavelet duration ** is equal to ** width / F / pi ** (Equation 2.7) Since F = f, assuming c = width and m = 2, temporal window = wavelet duration Holds. ** temporary window ** (by Roach & Mathalon (2008)) ** = wavelet duration ** (by field trip) looks good.
[Roach & Mathalon (2008)] 10 spectral bandwidth around any given center frequency is mσf Is this the same as the spectral bandwidth in [field trip] 9? From fieldtrip: spectral bandwidth = F / width * 2
If the previous width = c is correct, then c = f 0 </ sub> / σ f </ sub> (Equation 2.4) Because there is.
Roach & Mathalon (2008) spectral bandwidth = mσ f </ sub> = mf 0 </ sub> / c = F / width * m (fieldtrip equation) So, it can be said that m = 2 points to the same thing.
You can also say that fieldtrip's cfg.width = c (constant ratio).
There are too many terms. It's confusing. By the way, there is no explicit description corresponding to this "m" in the field trip. Is it processed appropriately internally?
-[Roach & Mathalon (2008)] 10 reference, but [Tallon-Baudry (1997)] 11 says, "wavelet duration 2σ t </ sub> of about two periods of oscillatory. The description "activity at f 0 </ sub>" appears. It seems that it is treated as m = 2 here as well. -[Ford et al (2008)] 14 in "constant ratio (σf = f / 7) and wavelet duration (4σ t </ sub>)" "spectral band with of 4σ f </ sub> >. It seems that cfg.width = 7 (constant ratio in other documents) in fieldtrip and m = 4 in [Roach & Mathalon (2008)] 10. -"m is recommended for 6, but there are also analysis examples for 4 and 2" ([Roach & Mathalon (2008)] 10).
MNE python --You can analyze the frequency with tfr_morlet, but there is a setting item like n_cycles. ――I don't know at all whether n_cycles points to c, temporary duration, or m in the description "The number of cycles globally or for each frequency." --When you look at the analysis examples, you can see 7 or 2 or freq / 2 or freq / 3. ――So I'm not sure after all. Since there is 7 in the setting example, it may be the same as cfg.width of fieldtrip, or so.
Reference: If you take a look at the morlet script that tfr_morlet uses internally
There is a def morlet in mne / time_frequency / tfr.py in the script
tfr.py
sigma_t = this_n_cycles / (2.0 * np.pi * f)
Therefore, from Eq. (2.5), I think that this_n_cycles (= n_cycles) = c (constant ratio).
Summary of 2
--cfg.width of fieldtrip and n_cycles of mne python, c (constant ratio. Equation 2.4) in the document, m in [stack overflow] 2 seems to point to the same thing. Understand the meaning of parameters " I can't, but I'd like to read the constant ratio and try to understand it as much as possible. Note that m in [Roach & Mathalon (2008)] 10 is different. --σ t </ sub> is temporary SD, which is different from wavelet duration (probably = temporary window). Wavelet duration = mσ t </ sub> ([Roach & Mathalon (2008)] [ From 10] --Similarly, σ f </ sub> is frequency SD, which is different from spectral bandwidth. Spectral bandwidth = mσ f </ sub> (from [Roach & Mathalon (2008)] 10) --Since I often see the setting of 7 including the explanation of constant ratio, it is better to see the setting of cfg.width and n_cycles first. -[Roach & Mathalon (2008)] m in 10 is not explicitly set in mne python, fieldtrip (I think). Fieldtrip is m = 2. Isn't mne equivalent? --There is an analysis example of n_cycles = 2 in mne python (it may be different from wavelet because it is an example of [source_band_induced_power] 12). It is still unknown whether it is the proper setting. [Roach & Mathalon (2008)] [ In 10], c is written as 5 or more, so it is possible that n_cycles = c is not from this deviation ... ――I don't really understand the difference between Morlet and complex morlet in the first place. So don't rely on this, let's hit the materials one by one.
Recommended Posts