Learn the basics of Theano once again
"Theano" is a framework of deep learning, but honestly it is quite difficult. In learning, I have been working with reference to the original Tutorial and Japanese commentary (also in Qiita), but it is difficult to understand. Here, we will check the basics of Theano again while moving a small code. (My environment at the moment is python 2.7.8, theano 0.7.0.)
How to use variables-symbolic and shared variables
In Theano, so-called variables are not directly manipulated, but relationships are described by symbols and deposited in the processing system, and input / output is performed after the processing system processes them as necessary. The fact that the automatic differentiation of the equation is included in this "processing" is a major feature of Theano.
First, let's use a normal symbolic variable.
import theano
import theano.tensor as T
a = T.dscalar('a')
b = T.dscalar('b')
c = a + 2 * b
f_1 = theano.function([a,b], c)
If you input up to this point and execute it, you will feel that the HDD is making a rattling noise and generating an intermediate file. After that, the defined function is executed.
>>> f_1(2,3)
>>> array(8.0)
So far, how to use Theano symbolic variables. Excerpts from the Theano documentation and a list of various variable types.
Theano Variables
| Variable type | Variables available |
|---|---|
| byte | bscalar, bvector, bmatrix, brow, bcol, btensor3, btensor4 |
| 16-bit integers | wscalar, wvector, wmatrix, wrow, wcol, wtensor3, wtensor4 |
| 32-bit integers | iscalar, ivector, imatrix, irow, icol, itensor3, itensor4 |
| 64-bit integers | lscalar, lvector, lmatrix, lrow, lcol, ltensor3, ltensor4 |
| float | fscalar, fvector, fmatrix, frow, fcol, ftensor3, ftensor4 |
| double | dscalar, dvector, dmatrix, drow, dcol, dtensor3, dtensor4 |
| complex | cscalar, cvector, cmatrix, crow, ccol, ctensor3, ctensor4 |
As mentioned above, the first character of the variables% scalar and% vector indicates the bit length of the variable. If this is omitted, the default value "float" and the bit length (variable type, dtype) will be floatX type (type that can be set by configuration).
Another thing to remember is ** shared variable **. Symbolic variables are rather "closed" variables in Theano, while shared variables are variables that are referenced by multiple functions and are used for things that are updated each time, such as learning parameters. Let's use this shared variable.
w = theano.shared(np.zeros(10), name='w')
print w.get_value()
As mentioned above, it is defined by theano.shared (initial value, symbol name in Theano). Also, unlike ordinary symbolic variables, shared variables can be retrieved with "get_value ()". (Conversely, in order to retrieve the value of a symbolic variable that is not a shared variable, it is necessary to prepare a function for that purpose.)
>>> print a # Theano Symbol
>>> a # I cannot see it
>>> print b # Theano Symbol
>>> b # I cannot see it...
>>> print w.get_value() # Theano Shared Variable
>>>[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
When declaring a shared variable in the constructor, there is an option to specify'borrow'.
s_default = theano.shared(np_array) #The default is borrow=False
s_false = theano.shared(np_array, borrow=False)
s_true = theano.shared(np_array, borrow=True)
This is an option that does not make a copy when creating a shared variable. (The original numpy object is destroyed.) (I don't understand it yet, so click here](http://deeplearning.net/software/theano/tutorial/aliasing.html#borrowing-when-creating-shared See -variables).)
Theano functions
The most important part of Theano. First, I will quote some writing styles. (The four sentences are irrelevant.)
>>> f = theano.function([x], 2*x)
>>> predict = theano.function(inputs=[x], outputs=prediction,
allow_input_downcast=True)
>>> linear_mix = theano.function([A, x, theano.Param(b, default=b_default)], [y, z])
>>> train = theano.function(
inputs=[x,y],
outputs=[prediction, xent],
updates=((w, w - 0.1 * gw), (b, b - 0.1 * gb)),
allow_input_downcast=True)
As mentioned above, theano.function () is described for a long time depending on how to add options.
The shortest format is as follows.
f = theano.function("input", "output")
So, List and tuple will be used for multiple inputs and outputs. (It seems that even one scalar type variable needs to be in list format to specify the input.) The following is a partial reprint of the explanation of the document.
function.function(inputs, outputs, mode=None, updates=None, givens=None, no_default_updates=False, accept_inplace=False, name=None, rebuild_strict=True, allow_input_downcast=None, profile=None, on_unused_input='raise')
Parameters -** params : Input values (required, inputs) - outputs **: Output values (required)
- mode
- updates
- givens
- no_default_updates
- name
- rebuild_strict
- allow_input_downcast
- profile
** updates ** are often used to update parameters as done in optimization calculations. Below is an example of using updates.
a = T.dscalar('a')
w2 = theano.shared(0.0, name='w2')
c = a + 2 * b + w2
f_3 = theano.function([a, b], c, updates=({w2: w2 + 1}))
#Or f_3 = theano.function([a,b],c, updates=[(w2, w2 + 1)])
for i in range(5):
print f_3(2, 3)
>>>
8.0
9.0
10.0
11.0
12.0
You can see that the contents of updates are reflected every time the function is called.
** gives ** is used to assign a concrete numerical value to a variable. In particular, it is used when assigning shared variables to theano functions. (If you give a shared variable with ** inputs **, an error will occur.)
w1 = T.dscalar('w1')
c = a + w1 * b
f_2a = theano.function([a, b], c, givens=[(w1, -2.0)])
print f_2a(2, 3)
>>> -4.0 # OK, c=a + w1 *to w1 of b-2.0 is assigned.
#If you specify a shared variable with inputs, an error will occur.
w2 = theano.shared(-2.0, name='w2') #w2 is a shared variable
f_2b = theano.function([a, b, w2], c) #The first argument is inputs
---------------------------------------------------------------------------
. . .
TypeError: Cannot use a shared variable (w2) as explicit input. Consider substituting a non-shared variable via the `givens` parameter
** allow_input_downcast ** is used to relax type management and avoid errors in situations where strict variable type management in Theano causes an error.
Finding the minimum value (without using T.grad ())
I would like to try to search for the minimum value of a function with the functions we have seen so far. As an example, with the function $ y = (x-1) ^ 4 $, I executed a code that monitors the amount of change in y while changing x and performs iterative calculation until the change falls below a predetermined threshold. (Since no differential value is used, it is not a gradient method.)
x_init = -1.0
x = theano.shared(x_init, name='x')
y = T.dscalar('y')
y = (x - 1.) ** 4
#Function f_4()Is defined. The increment value of x is specified by update.
f_4 = theano.function([], y, updates=({x: x + 0.01}))
# into loop
iter = 1000
y_prev = (x_init -1.1) ** 4
eps = 1.e-6
for i in range(iter):
y_update = f_4() ####In Loop, f_4()call.
y_delta = np.abs(y_update - y_prev)
if y_delta < eps:
x_min = x.get_value()
break
y_prev = y_update
print 'x_min = ', x_min
>>> x_min = 0.98999995552
As expected, we have calculated x_min, which gives the minimum value of the function $ y = (x-1) ^ 4 $. I haven't explicitly entered x for theano function f_4, but I can see that the ** updates ** option is working properly.
Try using automatic differentiation T.grad ()
Finally, it is T.grad () which is a feature of theano.
x = T.dscalar('x')
y = (x - 4) * (x ** 2 * 2+ 6) #Differentiated formula
#Differentiate y with respect to x
gy = T.grad(cost=y, wrt=x)
#Define a function to find the derivative,input:x,output: gy
f = theano.function(inputs=[x], outputs=gy)
print theano.pp(f.maker.fgraph.outputs[0])
#
print f(0)
print f(1)
print f(2)
>>>
((TensorConstant{1.0} * (((x ** TensorConstant{2}) * TensorConstant{2}) + TensorConstant{6})) + ((((TensorConstant{1.0} * (x - TensorConstant{4})) * TensorConstant{2}) * TensorConstant{2}) * (x ** TensorConstant{1})))
6.0
-4.0
-2.0
As mentioned above, the result of differentiating the mathematical formula given by print theano.pp (...) can be displayed. The y derivative value at each x (= 0, 1, 2) can also be calculated. For the time being, check the parameters that can be specified from the document.
theano.gradient.grad(cost, wrt, consider_constant=None, disconnected_inputs='raise', add_names=True, known_grads=None, return_disconnected='zero', null_gradients='raise')
Parameters: -** cost : Formula to be differentiated (required) - wrt **: Derivative coefficient (required)
- consider_constant
- disconnected_inputs
- add_name
- known_grads
- return_disconnected
- null_gradients
cost and wrt are required parameters.
Implement gradient descent
Now that I have a better understanding of the necessary parts, I will implement the gradient descent method. The target function is the Rosenbrock function, which is (likely) often used in benchmarking algorithms such as the gradient method.
Fig. Rosenbrock Function
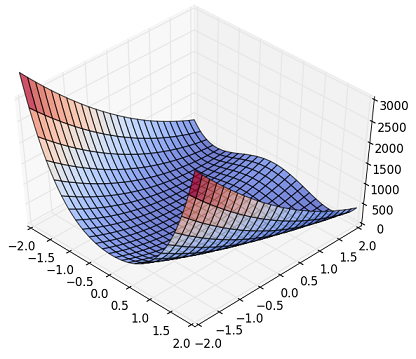
Although it is difficult to see in the above figure, it has a non-linearity that there is a groove in the annulus and Z suddenly rises when it deviates from the peripheral part. (There is a beautiful figure on Wikipedia, so if you are interested, please refer to it.)
The formula is as follows.
f(x, y) = (a - x)^2 + b * (y - x^2)^2
\ \ \ \\usually \ a\ = 1,\ and\ b\ =100
This function has a global minimum of $ f = 0.0 $ with $ (x, y) = (a, a ^ 2) $. The following code was created and executed.
import numpy as np
import theano
import theano.tensor as T
# Prep. variables and function
x_init = np.array([2.0, 2.0])
x = theano.shared(x_init, name='x')
a, b = (1., 100.)
# z_rb = (a - x) ** 2 + b * (y - x **2) **2
z_rb = (a - x[0]) ** 2 + b * (x[1] - x[0] **2) **2
dx = T.grad(cost=z_rb, wrt=x)
# Compile
train = theano.function(
inputs=[],
outputs=[z_rb],
updates=[(x, x-0.001 *dx)]
)
# Train
steps = 10000
print '(x,y)_init = (%9.3f, %9.3f)' % (x_init[0], x_init[1])
for i in range(steps):
z_tmp = train()
x_fin = x.get_value()
print '(x,y)_final= (%9.3f, %9.3f)' % (x_fin[0], x_fin[1])
>>>
(x,y)_init = ( 2.000, 2.000)
(x,y)_final= ( 1.008, 1.016)
The parameters (x, y) are summarized in a vector x [] of length 2. Starting from the initial value x = [2.0, 2.0], we were able to obtain a value close to the theoretical solution (1, 1). The figure below plots the history of x [](x, y).
Fig. Rosenbrock Function, contour

It can be seen that it is first swung to the left from (2., 2.) and then falls into the annular groove. (At first, when I calculated with the initial value (3., 3.), it diverged wonderfully ... By the way, the code of Numpy + scipy.optimize without using Theano is the initial value (3. , 3.) was also able to find the convergent solution. It seems that it is related to the optimal solution search algorithm rather than whether or not Theano is used.)
Once you understand this, you will be able to see the movement of the reference code that appears in Theano Tutorial. (Actually, I created a simple program for logistic regression and tried it.) Recently, "Chainer" has become popular, and the number of people who want to "learn Theano" may be decreasing. However, the first overseas Deep Learning related article dealing with Theano will continue to appear, and PyMC3 of the MCMC implementation library is also based on Theano, so I think it is important to deepen the understanding of Theano. There is.
References (web site)
- Theano Documentation http://deeplearning.net/software/theano/#documentation -[Qiita] Theano's basic memo http://qiita.com/mokemokechicken/items/3fbf6af714c1f66f99e9 --Theano's implementation of two-class logistic regression, a breakthrough on artificial intelligence http://aidiary.hatenablog.com/entry/20150519/1432038633 --SciPy Optimization documentation http://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html
- Wikipedia, Rosenbrock function https://en.wikipedia.org/wiki/Rosenbrock_function
Recommended Posts