I tried LeetCode every day 110. Balanced Binary Tree (Python, Go)
What is Leetcode
leetcode.com This is the practice of coding interviews for software developers. A total of more than 1,500 coding questions have been posted, and it seems that the same questions are often asked in actual interviews.
Introduction to golang + algorithm I will solve it with go and Python to strengthen the brain. (Python is weak but experienced)
25th question (question 110)
- Balanced Binary Tree
the issue's details
Given a binary tree, determine if it is height-balanced.
For this problem, a height-balanced binary tree is defined as:
a binary tree in which the left and right subtrees of every node differ in height by no more than 1.
(Japanese translation)
Given a binary tree, determine if it is height balanced.
In this problem, a height-balanced binary tree is defined as:
- A binary tree where the height of the left and right subtrees of all * nodes is 1 or less.
Example 1:
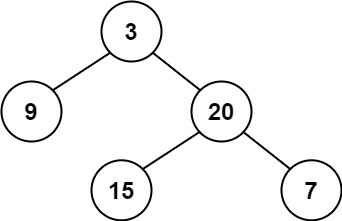
Input: root = [3,9,20,null,null,15,7]
Output: true
Example 2:
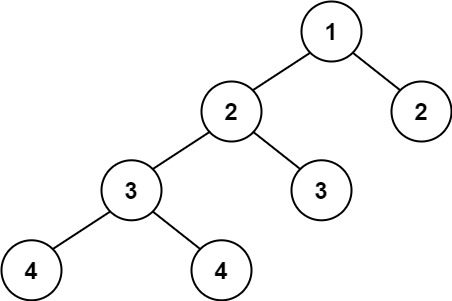
Input: root = [1,2,2,3,3,null,null,4,4]
Output: false
Example 3:
Input: root = []
Output: true
Way of thinking
-
Use a recursive function as a binary search
-
Measure the depth of the left node and the right node, and if there is a difference of 1 or more, return -1.
-
If the difference is less than 1 and left and right are not -1, return the deeper number as max.
-
Returns false if the final value is -1, true if not
Answer code
class Solution(object):
def isBalanced(self, root):
def check(root):
if root is None:
return 0
left = check(root.left)
right = check(root.right)
if left == -1 or right == -1 or abs(left - right) > 1:
return -1
return 1 + max(left, right)
return check(root) != -1
--I'll write it in Go too!
func isBalanced(root *TreeNode) bool {
if root == nil {
return true
}
lh := height(root.Left)
rh := height(root.Right)
if absDiff(lh, rh) > 1 {
return false
}
return isBalanced(root.Left) && isBalanced(root.Right)
}
func absDiff(a, b int) int {
if a >= b {
return a - b
}
return b - a
}
func height(root *TreeNode) int {
if root == nil {
return 0
}
return 1 + maxHeight(height(root.Left), height(root.Right))
}
func maxHeight(a, b int) int {
if a >= b {
return a
}
return b
}
Recommended Posts