Google translated http://scikit-learn.org/0.18/modules/multiclass.html [scikit-learn 0.18 User Guide 1. Supervised Learning](http://qiita.com/nazoking@github/items/267f2371757516f8c168#1-%E6%95%99%E5%B8%AB%E4%BB%98 From% E3% 81% 8D% E5% AD% A6% E7% BF% 92)

1.12. Multi-class algorithm and multi-label algorithm

** WARNING **: All scikit-learn classifiers provide ready-to-use multiclass classification. You do not need to use the sklearn.multiclass module unless you are experimenting with different multiclass strategies.

sklearn.multiclass Modules have become binary classification problems to solve multi-class and multi-label classification problems. We decompose these problems to achieve meta-estimation. Multi-target regression is also supported.

-** Multi-class classification ** means a classification task with two or more classes. For example, a set of images of fruits that can be oranges, apples or pears can be classified. Multiclass classification assumes that each sample is assigned to one and only label. The fruit is either an apple or a pear, but not both at the same time. -** Multi-label classification ** assigns a set of target labels to each sample. This can be thought of as predicting the properties of data points that are not mutually exclusive, such as topics related to the document. The text may be at the same time as or neither of religion, politics, finance, or education. -** Multi-output regression ** assigns a set of target values to each sample. This can be thought of as predicting some properties of each data point, such as the direction and magnitude of the wind at a particular location. -** Multi-output --Multi-class classification ** and ** Multi-task classification ** means that a single estimator must handle multiple co-classification tasks. This is a generalization of multi-label classification tasks that considers both binary classification as well as generalization of multi-class classification tasks. The output format is a two-dimensional array or sparse matrix.

The set of labels can vary from output variable to output variable. For example, you can assign a "pear" to a sample for an output variable that takes a possible value with a finite set of species such as "pear" or "apple". The second output variable "blue" or "green" ... which takes possible values in a finite set of colors such as "green", "red", "blue", "yellow" ...

This means that any classifier that handles multi-output multi-class tasks or multi-task classification tasks will support multi-label classification tasks as a special case. Multitasking is similar to a multioutput classification task with different model formats. See the appropriate estimator documentation for more information.

All scikit-learn classifiers are capable of multiclass classification, but the meta-estimator provided by sklearn.multiclass can change the way it handles more than one class. This is because it can affect the performance of the classifier (in terms of generalization error or required computational resources). The following is an overview of the classifiers supported by scikit-learn grouped by strategy. Unless you need custom multi-class behavior, you don't need a meta-estimation tool for this class if you're using any of these.

--Inherently multiclass: Naive Bayes, LDA and QDA, decision tree, random forest, nearest neighbor method, [sklearn.linear_model.LogisticRegression](http://scikit-learn.org/0.18/modules/generated/sklearn. Set multi_class ='multinomial' in linear_model.LogisticRegression.html # sklearn.linear_model.LogisticRegression). --Multi-label support: decision tree, random forest, nearest neighbor method.

One-Vs-One：sklearn.svm.SVC。 --One-Vs-All: All linear models except sklearn.svm.SVC.

Some estimators support multi-output-multi-classification tasks. Decision tree, random forest, nearest neighbor method.

** Warning: ** Currently, the metrics in sklearn.metrics are multi-output-multi-class classification task Not supported.

1.12.1. Multi-label classification format

In multi-label learning, the joint set of binary classification tasks is represented by a label binary indicator array. Each sample is a row of two-dimensional arrays (n_samples, n_classes) with binary values. That is, it is a non-zero element. A subset of labels An array such as np.array ([[1,0,0], [0,1,1], [0,0,0]]) is labeled 0, second in the first sample. Sample labels 1 and 2 and the third sample are unlabeled. It is more intuitive to generate multi-label data as a list of sets of labels. MultiLabelBinarizer Transformers allow you to convert label collections and indicator formats.

>>> from sklearn.preprocessing import MultiLabelBinarizer
>>> y = [[2, 3, 4], [2], [0, 1, 3], [0, 1, 2, 3, 4], [0, 1, 2]]
>>> MultiLabelBinarizer().fit_transform(y)
array([[0, 0, 1, 1, 1],
       [0, 0, 1, 0, 0],
       [1, 1, 0, 1, 0],
       [1, 1, 1, 1, 1],
       [1, 1, 1, 0, 0]])

1.12.2. One-Vs-The-Rest

This strategy is known as ** One-VS All ** and is known as OneVsRestClassifier Is implemented. The strategy is to fit one classifier per class. For each classifier, that class fits all other classes. In addition to its computational efficiency (only the n_classes classifier is needed), one advantage of this approach is its interpretability. Since each class is represented by one and only one classifier, it is possible to gain knowledge about that class by examining the corresponding classifier. This is the most commonly used strategy and is a fair default choice.

1.12.2.1. Multi-class learning

The following is an example of multi-class learning using OvR.

>>> from sklearn import datasets
>>> from sklearn.multiclass import OneVsRestClassifier
>>> from sklearn.svm import LinearSVC
>>> iris = datasets.load_iris()
>>> X, y = iris.data, iris.target
>>> OneVsRestClassifier(LinearSVC(random_state=0)).fit(X, y).predict(X)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

1.12.2.2. Multi-label learning

OneVsRestClassifier also supports multi-label classification. To use this feature, cell [i, j] sends an indicator matrix to the classifier indicating the presence of label j in sample i.

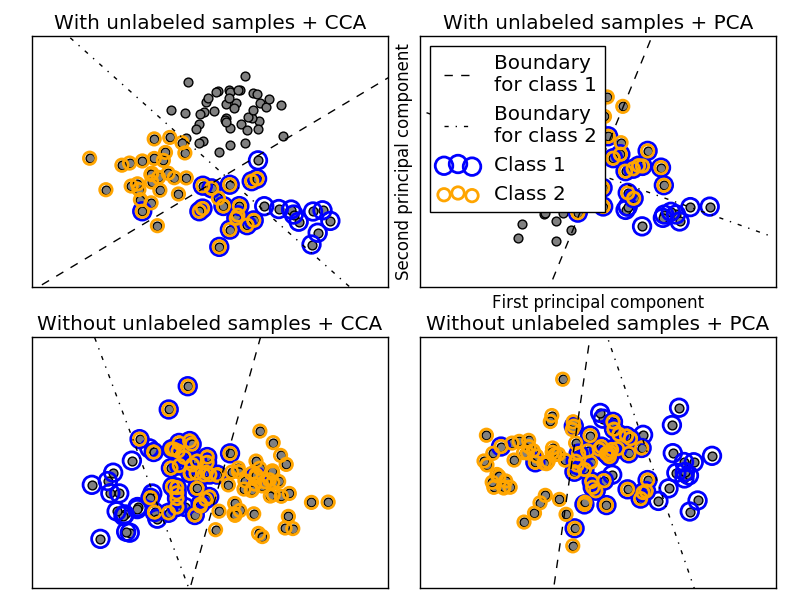
--Example: -Multi-label classification

1.12.3. One-Vs-One

OneVsOneClassifier builds one classifier for each pair of classes. At the time of prediction, the most voted class will be selected. If there is a tie (among two classes with the same number of votes), the class with the highest total classification confidence by adding the paired classification confidence levels calculated by the underlying binary classifier. Select. This method is usually slower than one-vs-the-rest due to its O (n_classes ^ 2) complexity, as the classifiers of n_classes * (n_classes -1) / 2 need to be fitted. Become. However, this method can be advantageous for algorithms such as kernel algorithms that do not fit well with n_samples. This is because each learning problem contains only a small subset of the data, while the rest of the pair uses the complete dataset n_classes times.

1.12.3.1. Multi-class learning

The following is an example of multi-class learning using OvO.

>>> from sklearn import datasets
>>> from sklearn.multiclass import OneVsOneClassifier
>>> from sklearn.svm import LinearSVC
>>> iris = datasets.load_iris()
>>> X, y = iris.data, iris.target
>>> OneVsOneClassifier(LinearSVC(random_state=0)).fit(X, y).predict(X)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 2, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

--Reference: -[1] "Pattern Recognition and Machine Learning. Springer", Christopher M. Bishop, page 183, (1st edition)

1.12.4. Error correction output code

Output-code-based strategies are quite different from one-vs-the-rest and one-vs-one. In these strategies, each class is represented in Euclidean space and each dimension is only 0 or 1. Alternatively, each class is represented by binary code (an array of 0s and 1s). The matrix that tracks the position / code of each class is called the codebook. The code size is the number of dimensions in space mentioned above. Intuitively, each class should be represented with as unique code as possible, and a good codebook should be designed to optimize classification accuracy. This implementation simply uses a randomly generated codebook as suggested in [3], but may add more complex methods in the future. At the time of fitting, one binary classifier is fitted for each bit in the codebook. At the time of prediction, the classifier is used to project a new point in class space and the class closest to the point is selected. OutputCodeClassifier uses the code_size attribute to use the classifier You can control the number of. This is a percentage of the total number of classes.

Numbers between 0s and 1s require fewer classifiers than the rest of the pair. Theoretically, log2 (n_classes) / n_classes can explicitly represent each class. However, log2 (n_classes) is much smaller than n_classes, which can actually reduce accuracy. Numbers greater than 1 require more classifiers than the remaining pair of classifiers. In this case, some classifiers theoretically correct errors made by other classifiers, hence the name "error correction". However, in practice this is not possible because classifier mistakes are generally correlated. The error correction output code has the same effect as bagging.

1.12.4.1. Multi-class learning

The following is an example of multi-class learning using output code.

>>> from sklearn import datasets
>>> from sklearn.multiclass import OutputCodeClassifier
>>> from sklearn.svm import LinearSVC
>>> iris = datasets.load_iris()
>>> X, y = iris.data, iris.target
>>> clf = OutputCodeClassifier(LinearSVC(random_state=0),
...                            code_size=2, random_state=0)
>>> clf.fit(X, y).predict(X)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1,
       1, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 2, 2, 2, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 1, 1, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

--Reference: -[2] "Solving multi-class learning problems with error correction output code", Dietterich T., Bakiri G., Journal of Artificial Intelligence Research 2, 1995. -[3] "Error Coding Methods and PICT", James G., Hastie T., Journal of Computational and Graphical statistics 7, 1998 -[4] "Elements of Statistical Learning", Hastie T., Tibshirani R., Friedman J., p. 606 (2nd edition) 2008.

1.12.5. Multi-output regression

You can add multi-output regression support to any regression analyzer that uses MultiOutputRegressor. This strategy consists of applying one regression factor for each goal. Since each target is represented by exactly one regression equation, it is possible to gain knowledge about the target by examining the corresponding regression equation. MultiOutputRegressor fits one regression equation per target, so you cannot take advantage of the correlation between targets. The following is an example of multi-output regression.

>>> from sklearn.datasets import make_regression
>>> from sklearn.multioutput import MultiOutputRegressor
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> X, y = make_regression(n_samples=10, n_targets=3, random_state=1)
>>> MultiOutputRegressor(GradientBoostingRegressor(random_state=0)).fit(X, y).predict(X)
array([[-154.75474165, -147.03498585,  -50.03812219],
       [   7.12165031,    5.12914884,  -81.46081961],
       [-187.8948621 , -100.44373091,   13.88978285],
       [-141.62745778,   95.02891072, -191.48204257],
       [  97.03260883,  165.34867495,  139.52003279],
       [ 123.92529176,   21.25719016,   -7.84253   ],
       [-122.25193977,  -85.16443186, -107.12274212],
       [ -30.170388  ,  -94.80956739,   12.16979946],
       [ 140.72667194,  176.50941682,  -17.50447799],
       [ 149.37967282,  -81.15699552,   -5.72850319]])

1.12.6. Classification of multiple outputs

Multiple output classification support can be added to any classifier that uses the MultiOutputClassifier. This strategy consists of adapting one classifier to each target. This allows for multiple target variable classifications. The purpose of this class is to train and estimate a set of objective functions (f1, f2, f3 ..., fn) with one X predictor matrix and then set a set of (y1, y2, y3 ..., yn). Is to extend the estimator so that it can predict the prediction of.

The following is an example of multi-output classification.

>>> from sklearn.datasets import make_classification
>>> from sklearn.multioutput import MultiOutputClassifier
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.utils import shuffle
>>> import numpy as np
>>> X, y1 = make_classification(n_samples=10, n_features=100, n_informative=30, n_classes=3, random_state=1)
>>> y2 = shuffle(y1, random_state=1)
>>> y3 = shuffle(y1, random_state=2)
>>> Y = np.vstack((y1, y2, y3)).T
>>> n_samples, n_features = X.shape # 10,100
>>> n_outputs = Y.shape[1] # 3
>>> n_classes = 3
>>> forest = RandomForestClassifier(n_estimators=100, random_state=1)
>>> multi_target_forest = MultiOutputClassifier(forest, n_jobs=-1)
>>> multi_target_forest.fit(X, Y).predict(X)
array([[2, 2, 0],
       [1, 2, 1],
       [2, 1, 0],
       [0, 0, 2],
       [0, 2, 1],
       [0, 0, 2],
       [1, 1, 0],
       [1, 1, 1],
       [0, 0, 2],
       [2, 0, 0]])

[scikit-learn 0.18 User Guide 1. Supervised Learning](http://qiita.com/nazoking@github/items/267f2371757516f8c168#1-%E6%95%99%E5%B8%AB%E4%BB%98 From% E3% 81% 8D% E5% AD% A6% E7% BF% 92)

[Translation] scikit-learn 0.18 User Guide 1.12. Multi-class algorithm and multi-label algorithm