[Translation] scikit-learn 0.18 User Guide 4.5. Random projection
Google translated http://scikit-learn.org/0.18/modules/random_projection.html [scikit-learn 0.18 User Guide 4. Dataset Conversion](http://qiita.com/nazoking@github/items/267f2371757516f8c168#4-%E3%83%87%E3%83%BC%E3%82%BF From% E3% 82% BB% E3% 83% 83% E3% 83% 88% E5% A4% 89% E6% 8F% 9B)
4.5. Random projection
sklearn.random_projection Modules are a controlled amount for faster processing times and smaller model sizes Implements a simple and computationally efficient way to reduce the dimensions of your data by trading the accuracy of (as an additional variance). This module implements two types of unstructured random matrices, Gaussian random matrices and Sparse random matrices. The dimensions and distribution of the random projection matrix are controlled to preserve the paired distance between any two samples in the dataset. Therefore, random projection is a good approximation technique for distance-based methods.
- References:
- Sanjoy Dasgupta. Experiment with random projection. Minutes of the 16th Conference on the Uncertainty of Artificial Intelligence (UAI'00), Craig Boutilier and Moisés Goldszmidt (Eds.). Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 143-151.
- Ella Bingham and Heiki Mannilla 2001 [Random projection in dimensionality reduction: application to image and text data](http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.24.5135&rep=rep1&type = pdf) Lecture at the 7th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD'01) ACM, New York, NY, USA, 245-250.
4.5.1. Johnson-Lindenstrauss Lemma
The main theoretical result of the efficiency of random projection is Johnson Lindenstrauss Lemma (Wikipedia quoted).
In mathematics, Johnson-Lindenstrauss's lemma is the result of low-distortion embedding of points in high-dimensional to low-dimensional Euclidean space. The lemma states that small sets of points in higher dimensional space can be embedded in much lower dimensional space so that the distance between points is largely preserved. The map used for embedding is at least Lipschitz and can also be considered an orthodox projection.
sklearn.random_projection.johnson_lindenstrauss_min_dim knows only the number of samples. It conservatively estimates the minimum size of the artificial subspace and guarantees bounded distortion introduced by random projection.
>>> from sklearn.random_projection import johnson_lindenstrauss_min_dim
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=0.5)
663
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=[0.5, 0.1, 0.01])
array([ 663, 11841, 1112658])
>>> johnson_lindenstrauss_min_dim(n_samples=[1e4, 1e5, 1e6], eps=0.1)
array([ 7894, 9868, 11841])
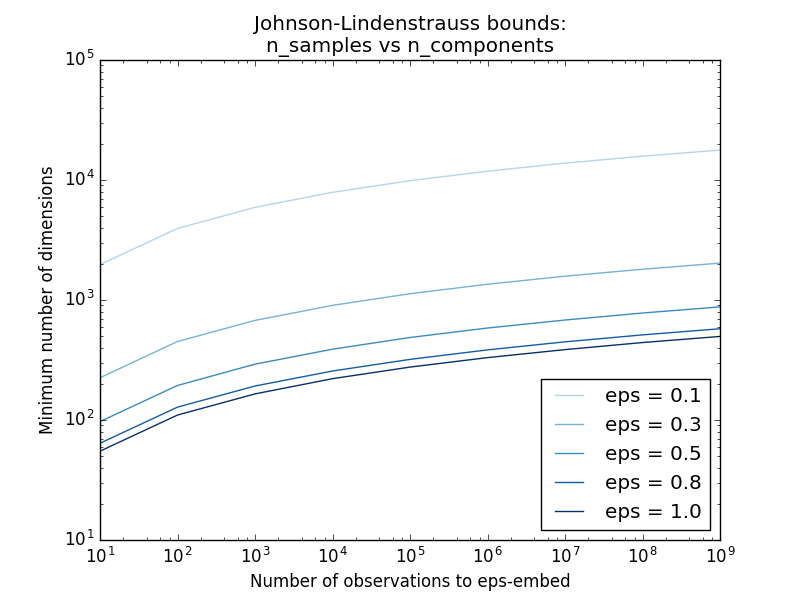
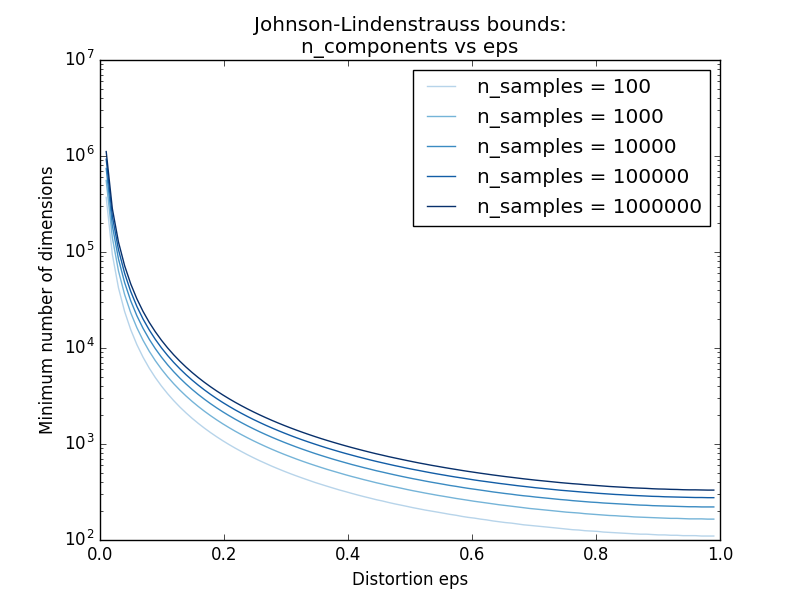
- Example:
- See the theoretical commentary on the Johnson-Lindenstrauss lemma and the Johnson-Lindenstrauss for random projection embedding for empirical verification using sparse random matrices.
- References:
- Sanjoy Dasgupta and Anupam Gupta, 1999. Basic evidence of the Johnson-Lindenstrauss lemma.
4.5.2. Gaussian random projection
sklearn.random_projection.GaussianRandomProjection projects the original input space onto a randomly generated matrix to reduce the dimensions. Here, the components are derived from the following distribution $ N (0, \ frac {1} {n_ {components}}) $. Here is a small excerpt showing how to use the Gauss random projection transformer:
>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100, 10000)
>>> transformer = random_projection.GaussianRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)
4.5.3. Sparse random projection
sklearn.random_projection.SparseRandomProjection is the original input using a sparse random matrix Reduce dimensions by projecting space.
The sparse random matrix is an alternative to the dense Gaussian random projection matrix, guaranteeing similar embedding quality, being more memory efficient, and enabling fast computation of projected data.
If you define s = 1 / density, the elements of the random matrix will be
\left\{
\begin{array}{c c l}
-\sqrt{\frac{s}{n_{\text{components}}}} & & 1 / 2s\\
0 &\text{with probability} & 1 - 1 / s \\
+\sqrt{\frac{s}{n_{\text{components}}}} & & 1 / 2s\\
\end{array}
\right.
Where $ n_ {\ text {components}} $ is the size of the projected subspace. By default, the density of nonzero elements is set to the following minimum density recommended by Ping Li et al. $ 1 / \ sqrt {n_ {\ text {features}}} $
A small excerpt showing how to use a sparse random projective transformation:
>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100,10000)
>>> transformer = random_projection.SparseRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)
- References:
- D. Achlioptas Database-friendly random projection: Johnson-Lindenstrauss and binary coins Computer Systems Science 66 (2003) 671-687
- Ping Li, Trevor J. Hastie, and Kenneth W. Church 2006 [Very sparse random projection](http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.62.585&rep=rep1&type= pdf) Lecture at the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD '06) ACM, New York, NY, USA, 287-296.
[scikit-learn 0.18 User Guide 4. Dataset Conversion](http://qiita.com/nazoking@github/items/267f2371757516f8c168#4-%E3%83%87%E3%83%BC%E3%82%BF From% E3% 82% BB% E3% 83% 83% E3% 83% 88% E5% A4% 89% E6% 8F% 9B)
© 2010 --2016, scikit-learn developers (BSD license).