[Mathematics] If you understand the meaning of "inner product" graphically, you can see various things.
When you start studying linear algebra, it comes out quite quickly, inner product. The calculation itself is not so difficult, but I think there are people who don't get it right. Me too, I was like that. So, in this visualization series, I will focus on the "inner product".
In addition, there are things that can be understood by the inner product everywhere in statistics, and it becomes "inner product": grin :. A vector is a sequence of data, so it is very related to statistics. It will be treated in statistics from the next time, but first from the inner product.
0. A little conclusion first
Since the previous theory is necessary, I would like to write only the conclusion of the meaning of the inner product first. The inner product can be written as a mathematical formula as follows.
{\bf a}\cdot{\bf b} = \|{\bf a}\|\|{\bf b}\|\ \cos\theta
To express it visually, it becomes as follows, and it can be given the meaning of the length of the vector $ {\ bf a} $ multiplied by the length of the vector $ {\ bf c} 
So far, if you say "Yeah, that's right", please wait for a while as I will explain how the inner product is handled well in statistics next time. (Since the slide version has already been explained, please see ** here ** until then)
If you want to know "why you can say this" and "what this is", I would like to explain it from now on, so please proceed as it is.
1. Definition and calculation of inner product
Let's start with the mathematical definition. When there is a vector $ {\ bf a} = (a_1, \ cdots, a_n), {\ bf b} = (b_1, \ cdots, b_n) $, its inner product is defined as follows.
{\bf a} \cdot {\bf b} = a_1b_1+\cdots+a_nb_n = \sum_{i=1}^n a_ib_i
It means multiplying the corresponding elements of each vector element (the first element $ a_1 $ and the first element $ b_1 $ correspond etc ...) and adding them all together. Let's consider the visual meaning of this.
2. Application of the law of cosines
To understand the inner product, we use what is called the cosine theorem. The formula is below.
\|{\bf b}-{\bf a}\|^2 = \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2\|{\bf a}\|\|{\bf b}\|\ \cos\theta \cdots (*)

The relationship between the lengths of each side of the triangle as described above satisfies this formula relationship.
Also, the square of the length of $ {\ bf a} $
\|{\bf a}\|^2 = \left(\sqrt{a_1\cdot a_1 + \cdots + a_n\cdot a_n}\right)^2 =a_1\cdot a_1 + \cdots + a_n\cdot a_n\\
=\sum_{i=1}^n x_i^2 = {\bf a} \cdot {\bf a}
Can be represented by the dot product of the same vector.
this
\|{\bf b}-{\bf a}\|^2 = ({\bf b}-{\bf a})\cdot({\bf b}-{\bf a}) = {\bf a}\cdot{\bf a} + {\bf b}\cdot{\bf b} - 2 {\bf a}\cdot{\bf b} \\
= \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2 {\bf a}\cdot{\bf b}
Substituting this into the (*) equation of the cosine theorem
\|{\bf b}-{\bf a}\|^2 = \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2\|{\bf a}\|\|{\bf b}\|\ cos\theta\\
\Rightarrow \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2 {\bf a}\cdot{\bf b} = \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2\|{\bf a}\|\|{\bf b}\|\ cos\theta\\
On both sides
- 2 {\bf a}\cdot{\bf b} = - 2\|{\bf a}\|\|{\bf b}\|\ cos\theta \\
\Rightarrow {\bf a}\cdot{\bf b} = \|{\bf a}\|\|{\bf b}\|\ cos\theta
So, the inner product is
\|{\bf a}\|\|{\bf b}\|\ \cos \theta
It turned out to be.
Wow, I see ...? ?? ??
So what? I'm feeling···
But this shape is very important, so please remember it.
Then this
3.||a|| ||b||Explore the mystery of cosθ#
3.1 Reconfirmation of cos θ and the concept of projection
First of all, I would like to reconfirm $ \ cos \ theta $ once again. The mathematical definition is
\cos \theta = \frac{\|c\|}{\|r\|}
is. As shown in the graph,

$ r $ is the radius and $ x $ is the vector from the vector $ r $ to that point, drawing a line perpendicular to the x-axis. As an image, as shown below, it is the part that illuminates the light from directly above and becomes a shadow. (It's called projection.) ** The shadow part created by illuminating the roof $ {\ bf r} $ is the vector $ {\ bf c} $. ** **

3.2 Meaning of inner product
\|c\| = \|r\|\cos \theta
So the length of c is
By the way, here was the homework of the previous section
\|{\bf a}\|\|{\bf b}\|\ \cos \theta
Let's get back to. Similarly, try shining a light from above.

vector
{\bf a}\cdot{\bf b} = \|{\bf a}\|\|{\bf b}\|\ \cos\theta
So, ** "length of vector $ {\ bf a} $" ** and ** "length of vector $ {\ bf b} $ projected onto vector $ {\ bf a} $" It is considered to be the product of **.
Since the inner product is also ** "product" **, it is some kind of multiplication, but I think that the image of ** multiplication between vectors should be the image of matching the directions and multiplying the length **. I am.
3.3 When the directions of the two vectors are vertical
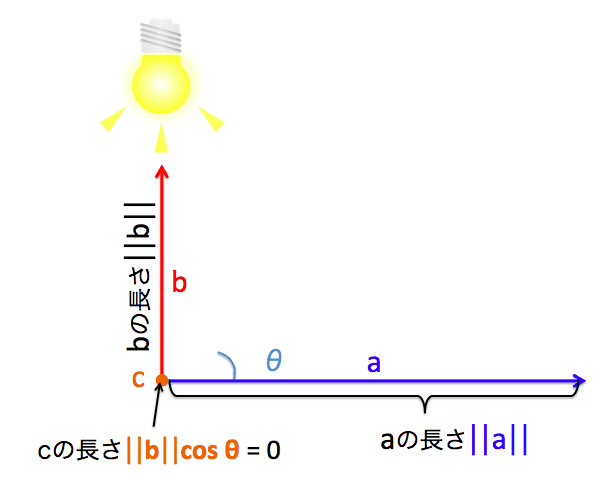
If the angles of the two vectors are right angles, you can't cast a shadow even if you shine a light from above. Therefore, at this time, the length of the vector $ {\ bf c} $ becomes 0. In other words, when the angle is right angle, the inner product is also 0.
3.3 For a vector of length 1
Make the story easier
\cos \theta = \frac{\|c\|}{\|r\|} = \|c\|
Therefore, the length of $ {\ bf c} $ becomes the value of $ \ cos \ theta $ as it is.
 Now, if you look at the inner product of $ {\ bf x} $ and $ {\ bf r} $,
Now, if you look at the inner product of $ {\ bf x} $ and $ {\ bf r} $,
{\bf x}\cdot{\bf r} = \|{\bf x}\|\|{\bf r}\|\ \cos\theta = 1 \cdot 1 \cdot \cos\theta = \cos\theta
Therefore, the inner product of two vectors with lengths of 1 is $ \ cos \ theta $ **: smile:
In the next article, I will write about "scenes where inner products are used in statistics". We will explain how the variance / standard deviation, covariance / correlation coefficient, regression coefficient, etc. look in relation to this inner product using graphs and animations in Python.
Recommended Posts