This article is the article on 12/21 of WACUL Advent Calendar 2016.

Hello, the data sign en steam of WACUL, is @onhrs that the work of data analysis.

Most recently, I have been working on natural language processing and other data analysis related to machine learning.

This time, Professor Hidetoshi Nishimori and Professor Masayuki Ozeki [Quantum Computer Accelerates Artificial Intelligence](https://www.amazon.co.jp/ Quantum Computer Accelerates Artificial Intelligence-Nishimori-Hidetoshi / dp /4822251896/ref=sr_1_1?ie=UTF8&qid=1481941470&sr=8-1&keywords=Nishimori%E3%80%80 Quantum), so I read ** Artificial Intelligence x Quantum Computer ** in line with the contents of the book. I want to talk about. (We aimed for people who do not understand physics and mathematics to understand it.)

I also tried to give an overview using Python without using mathematical formulas. Even if I don't understand the details, I tried to make it visually visible and understandable.

I am motivated to post articles other than Advent Calendar, so I would be grateful if you would like it. (Lol)

Target audience of this article

・ Those who want to know about quantum computers and quantum annealing ・ Those who want to know the current status and future potential of quantum computers ・ Those who want to know the relationship between quantum computers and artificial intelligence ・ Those who want to get started with data science in Python

Expected environment

Language: Python3 You need NumPy, SciPy, matplotlib, etc., but you can add Anaconda.

Editor: Jupyter (Of course, other editors are fine)

As a keyword

I think there will be esoteric words and unfamiliar terms. Here is a summary of the important words, keywords and their brief overviews for preparation and for later review. (It's okay if there are words you don't understand at this point. In that case, skip them.)

The order is appropriate.
It is not a strict definition, but rather, there are places where you are lying because you are pursuing clarity, but please reconstruct it after understanding it. (Laughs) In order to have a proper understanding, it is essential to understand ** statistical mechanics ** and ** quantum mechanics **.

Machine learning

It's harder to explain as easily as these words, but the point is to use statistical techniques to find the patterns that can be obtained from them. This is an indispensable method for current big data analysis.

Deep learning (or deep learning)

A method of performing machine learning using a method that imitates the brain (neural network).

It is very useful when you have a lot of data, including image judgment.

Strictly speaking, it does not necessarily have to be a multi-layer structure or deep learning must be a neural network structure.

Quantum computer

Unlike conventional computers that perform calculations with binary numbers of '0' and '1', quantum mechanics is a'** wave **' that occurs in the microscopic (extremely expanding) world of atoms and molecules. A computer that uses the properties of.

Quantum annealing

An optimization problem, a method that uses the above-mentioned quantum mechanics wave phenomenon to calculate high-speed calculations that would take a long time if all paths were calculated. Also called quantum annealing.

Qubit

While ordinary bits can only represent '0' and '1', qubits are waves, as mentioned above, so they can be superposed. You can express the ambiguity of being 1 and 0. (Details can be understood by understanding quantum entanglement.)

Quantum entangle

It is the quantum state of superposition itself. Matter is also a wave in the quantum world, so it is superposed, so it is the state itself. (Maybe this is the understanding.)

To put it in a difficult way, when considering two particles (waves), it is the correlation that they receive from each other. If one state is determined, the other state is also determined. Quantum teleportation uses this phenomenon.

Simulated annealing

It is derived from the phenomenon of "annealing", which is a phenomenon in which the crystal structure becomes beautiful when the temperature is slowly lowered while the metal is at a high temperature. This is a classical way to solve the crystallization problem.

Quantum gate method

A method in which a qubit is embedded in a semiconductor and calculated. Conventional quantum computers often refer to this method, but with the advent of quantum annealing quantum computers, the position has been reversed.

This quantum gate type quantum computer did not go well because the quantum state was liable to collapse.

Tunnel effect

In the quantum state, matter can be thought of as a wave, which is a stochastically determined wave, and in certain situations there is a situation where it "passes through" rather than overcomes an energy barrier.

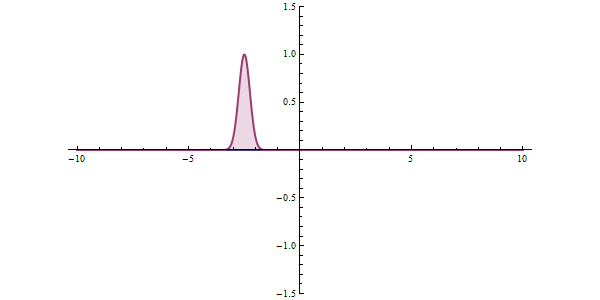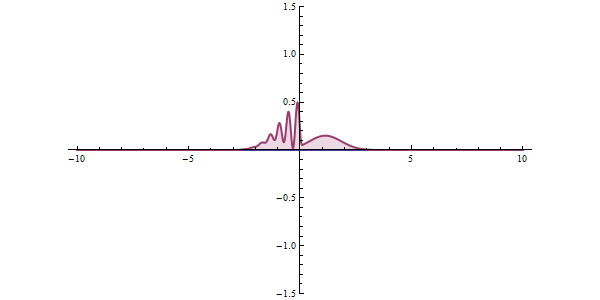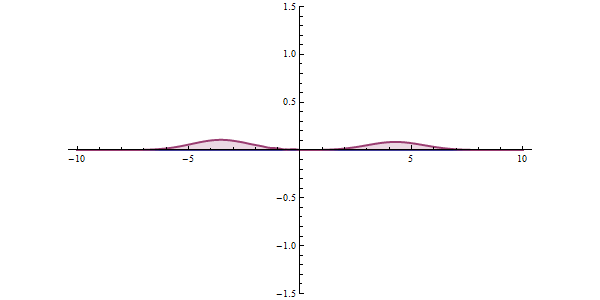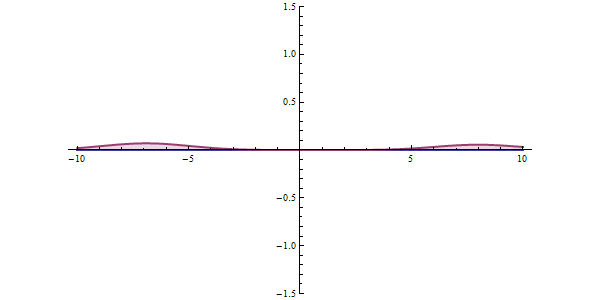
https://ja.wikipedia.org/wiki/%E3%83%88%E3%83%B3%E3%83%8D%E3%83%AB%E5%8A%B9%E6%9E%9C

spin

It is the smallest unit of a magnet. The electron, which is the smallest unit of electric current, has the property of rotation. This is to rotate. Expressed as (upward, downward) or (clockwise, counterclockwise)

~~ It seems that people who specialize in elementary particles will get really angry (laughs) ~~ Let's proceed without worrying about it.

Ising model

It is a model for realizing quantum annealing, and it is possible to make the state that minimizes the energy state of the above spins the solution of the optimization problem.

D-Wave

A company that put into practical use the theory of Professor Nishimori, who advocated quantum annealing, and produced the world's first commercial quantum computer.

About the traveling salesman problem that cannot be solved even with a supercomputer

In considering the traveling salesman problem, a salesman considers the route that minimizes the distance when traveling to multiple cities.

For example, three cities (eg Tokyo, Nagoya and Osaka) Tokyo → Osaka → Nagoya → Tokyo and Tokyo → Nagoya → Osaka → Tokyo, It seems to be considered the same when going in the opposite direction, so it is 1 for 3 cities.

[Quantum Computer 1] Dream Machine Suddenly Commercialized (3/6)

To generalize

\frac{(n-1)!}{2}Street

is. So if you write it in Python (I don't think you need to write it)

#Traveling salesman problem
import math

def travelingSales(n):
    return math.factorial(n-1)/2

With this, 8 cities

travelingSales(8)
2520

In 15 cities

travelingSales(15)
43589145600.0(45.3 billion)

In 20 cities

travelingSales(20)
6.0822550204416e+16

In 30 cities

travelingSales(30)
4.420880996869851e+30

…

It will be. Up to 20 cities can be solved in a few seconds with a supercomputer, but in 30 cities it takes 14 million years, which is too long.

The above is the outline of the traveling salesman problem.

Reference: [Quantum Computer 1] Dream Machine Suddenly Commercialized: ITpro

Then what should I do?

In practice, there are several ways to calculate various approximations to solve the above problem, but we will focus on simulated annealing, which is related to quantum annealing.

First of all, if you summarize the current situation briefly, it seems that human beings can understand a simple shortest path, but since the computer has to take the trouble to calculate the shortest path after considering all the combinations of routes, Even if there were about 30 cities, the route itself was innumerable and could not be solved.

In order to explain a concrete example, I will explain with reference to the official document of Scipy.

"Optimization problems are problems that find numerical solutions of minimum values and equations. The scipy.optimize module is a function (scalar or multidimensional) function minimization and curve fitting, And it provides a convenient algorithm for root search. (From Official Document)

Plot the optimization problem using optimize.fmin_bfgs using the BFGS algorithm and actually calculate it.

Let's define the following function and actually solve the optimization problem.

f(x)=x^2+15sin(1.2x) \\ (-10\leqq x\leqq10)

from scipy import optimize

def minfunc(x):
    return x**2+ 15*np.sin(1.2*x)


x = np.arange(-10, 10, 0.1)
plt.plot(x, minfunc(x))

You can easily find it by setting optimize.fmin_bfgs (function, initial value, disp = 0).

#disp=0 gives only the minimum value
optimize.fmin_bfgs(minfunc, 0,disp=0)

The value obtained is

array([-1.19776296])

Certainly, the minimum value that can be visually recognized was obtained.

However, tentatively in the second argument of optimize.fmin_bfgs

#Initial value x=-Set to 5
optimize.fmin_bfgs(minfunc, -5, disp=0)
array([-5.94383045])

#Initial value x=Set to 3
optimize.fmin_bfgs(minfunc, 3, disp=0)
array([ 3.58552219])

#Initial value x=Set to 10
optimize.fmin_bfgs(minfunc, 10, disp=0)
array([ 8.20653212])

Then, it will be as above.

From the initial value, only the value of y when the differential coefficient is 0 (the place where the ball is trapped in the dent when the ball is rolled from the specified place) can be obtained.

Applying to the traveling salesman problem, assuming that the vertical direction of the graph is the distance that travels around the city and the horizontal axis is the number of patterns that travel around the city (I think it's a bit aggressive), $ (-10 ) For all leqq x \ leqq10) $, take optimize.fmin_bfgs as an example, try various initial values, and the lowest value is the minimum value (that is, the minimum value of the distance traveled around the city). is.

After all, if you look for it thoroughly, it will be difficult to solve it when it reaches the amount of 30 patterns like the traveling salesman problem.

To solve the above problems, there is a technique called simulated annealing.

In simulated annealing, a stochastic distribution is given, the distribution is made large at first, and then the distribution of probabilities is gradually narrowed (this work is the part that gradually lowers the temperature of the conventional "annealing". Even if it is trapped in the above example (differential coefficient is 0), it does not finish the calculation at that point and goes to find the final minimum value.

However, even with this method, it seems that the calculation is less than the squeeze calculation, but in the case of a complicated problem, a huge amount of calculation is required and a large amount of energy is required to escape the trap. will be needed.

In quantum annealing, this is solved by the quantum phenomenon ** tunnel effect **.

In addition to the stochastic search of simulated annealing, by searching in the quantum state wave, it is possible to create a tunnel effect from the trapped position and easily move to the minimum value.

As described above, it seems that it is possible to calculate the traveling salesman problem by using the quantum effect for the conventional simulated annealing. (In "Quantum computer accelerates artificial intelligence", it was written that it would be "100 million times".)

The tunnel effect stochastically exudes a wave of particles when certain conditions are met, so it is unlikely that a tunnel will fall to the optimum solution, but the reason for this is an individual's. As a homework, I would like to find out at a later date.

Ising model that actually enables quantum annealing

Then, in fact, there is an "Ising model" as a model to solve the optimum solution under the situation that enables quantum annealing.

When viewed in terms of atomic size, the property of spin, which is the smallest unit of a magnet, appears. Actually, they are small and disjointed, so they are usually invisible, but in a special state, the spins are aligned, and as a result, the properties of a magnet are born. (* The study of "magnetism" in the field of magnets is extremely difficult !!)

This property of spin has only two states, upward and downward. (For those who know, the energy state of the quantized state can only take discrete values.)

The Ising model is a model that calculates using this property of "spin" that can be seen when it is small. (I will omit the story of interaction and the formula itself to calculate the Ising model because it is difficult.)

I don't know what you're talking about in the explanation so far, so let's take a concrete look.

To simplify the calculation, we will reduce the dimensions and discuss in two dimensions. (In short, let's discuss in the world of anime without depth.)

The original story is I will explain the Ising Model in a simple way And Monte Carlo Simulation of the Ising Model using Python with Ising model in Python Since it is implemented, refer to that (especially, the former code was explained and improved).

To animate, I use Matplotlib's ArtistAnimation to record multiple images in an array ims and actually run them with ArtistAnimation. http://qiita.com/yubais/items/c95ba9ff1b23dd33fde2

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from pandas import Series, DataFrame
from numpy.random import randint, randn, rand
import math
import matplotlib.animation as animation


#Play matplotlib animation on Jupyter
%matplotlib nbagg

#Number of atoms
Size = 50 

#J is a constant that represents the interaction between spins
J = 1

#magnetic field
H = 0

#temperature[K]
Temp = 0


#Does the spin reverse?
def spin_direction(field, x, y):
    energy = H

    '''
Periodic boundary conditions
(Because the atom located at the edge does not touch the four atoms,
Only in that case is it translated.)
    '''
    for dx, dy in [(-1,0), (1,0), (0,-1), (0,1)]:

        if x + dx < 0: 
            dx += Size
        if y + dy < 0: 
            dy += Size
        if x + dx >= Size: 
            dx -= Size
        if y + dy >= Size: 
            dy -= Size

        #Energy calculation
        energy += J * field.iloc[x + dx, y + dy]

    if Temp == 0:
        #np.sign is 1 for positive and 1 for negative for each element-Returns 0 if it is 1 or zero.
        p = (np.sign(energy) + 1) * 0.5
    else:
        #Probability of spin reversal with temperature and energy (T)=(Except when it is 0)
        p = 1/(1+np.exp(-2*(1/Temp)*energy))
        #Whether the spin calculated above has a higher probability of inversion than a floating point random number between 0 and 1.
    if rand() <= p:
        spin = 1
    else:
        spin = -1
    return spin





#I don't know much about Gibbs Sump Ring.
def run_gibbs_sampling(field, iternum=5):
    for _ in range(iternum):
        lattice = DataFrame([(y,x) for x in range(Size) for y in range(Size)])

        #Reindex re-assigns the position of the atom appropriately
        lattice = lattice.reindex(np.random.permutation(lattice.index))

        #lattice.values is the position of each grid point. For example[0,0]If so, 0th vertically and 0th horizontally
        for x, y in lattice.values:

            #Calculate if the spin is reversed
            field.iloc[x, y] = spin_direction(field, x, y)




fig = plt.figure()
field = DataFrame(randint(2,size=(Size,Size))*2-1)

temps = [0.,.5,1.,1.5,2.,2.5,5.0,10.0][::-1]

ax1=fig.add_subplot(1,2,1)
ax2=fig.add_subplot(1,3,3)
ax2.axis(xmin=-1,xmax=10.5)
ax2.set_xlabel("time")
ax2.set_ylabel("T[K]")


ims = []


for i in range(1,9):

    Temp = temps[i-1]
    run_gibbs_sampling(field)
    im1 = ax1.imshow(field.values, vmin=-1, vmax=1,cmap=plt.cm.gray_r, interpolation='nearest')
    x=np.arange(1, 9, 1)
    im2,=ax2.plot(x[0:i], temps[0:i],marker="o",markersize=12,color = "red")

    ims.append([im1,im2])

ani = animation.ArtistAnimation(fig, ims, interval = 1000)

#Save destination (if necessary)
#ani.save("ising.gif")

plt.show()

As the temperature approaches 0K (absolute temperature is −273.15 $ {} ^ \ circ \ mathrm {C} $ is 0K), the disjointed spin states become stable (that is, low energy states). You can see how the upward and downward directions are localized.

The true stable state is that everything is up or down, but because they are stochastically disjointed (more precisely, disjointed by the vibration of atoms due to temperature), they happen to be next to each other when the temperature drops. Since spins have the property of facing the same direction, some of them are localized.

Spin interaction is determined by the size of J.

When a magnetic field is applied (assuming that the magnet is brought closer), it is only necessary to execute (H = 0.5 in the above code).

Here, due to the force of the magnetic field, they all face the same direction near T = 2K.

As before, you can see that things that happened to be localized are all oriented in the same direction before they are localized with the assistance of the magnetic field.

So far, we have explained about the 2D Ising model. (It was long.)

According to this model, quantum annealing is an application of an optimization problem that actually applies the stable state of the spin of a substance.

The actual quantum computer is a three-dimensional extension of the above Ising model. Extending to this model, the spin mysteriously has only two states, up and down.

By applying a magnetic field from the side to a substance that is a three-dimensional extension of the Ising model, a superposition state (quantum entanglement state) of spins upward and downward is created.

By gradually lowering this transverse magnetic field in the same way as the temperature was lowered earlier, the spin interaction between atoms becomes larger, and the minimum value at which the spin energy state when the transverse magnetic field is 0 is to be solved. It is said to take.

As described above, by performing the spin superposition (entanglement) state with an actual substance, the optimization problem that requires a huge amount of calculation even in simulated annealing can be solved by the quantum phenomenon (especially the tunnel). It is realized by the effect).

I tried to draw a figure myself, but I was exhausted. For details, see the site I introduced earlier. (May be edited and updated later) http://itpro.nikkeibp.co.jp/article/COLUMN/20140514/556566/

Is it related to machine learning and deep learning?

It is expected to be applied in the fields of machine learning and deep learning, and AI (or machine learning) has rapidly developed in recent years, such as investment portfolio optimization problems, image authentication, medical care, law, and archeology. In the field of, this quantum computer seems to be able to accelerate them. In addition, with the advent of D-wave, google is seriously trying to realize a quantum computer with this method, and it can be said that the application fields by quantum annealing are very diverse. (For more details about this area, please refer to Professor Nishimori's "Quantum Computer Accelerates Artificial Intelligence".)

At the end

As a retrofit, I am currently working as a data scientist in the analysis of big data (mainly web data) using AI (machine learning or statistics), but I am a graduate school. So, I was researching a spin transistor, an element that realizes a quantum gate type quantum computer.

AI and quantum computers, which were thought to be unrelated at the time, have begun to be involved in recent years, and it was surprising that quantum computers play an important role in the realization of true AI. (University research was not wasted.)

Also, quantum mechanics and Ising model are still really deep, so I decided to take this opportunity to study more. (Now, I was frustrated at that time [Statistical Physics of Landau](https://www.amazon.co.jp/%E7%B5%B1%E8%A8%88%E7%89%A9%E7%90%86] % E5% AD% A6-% E4% B8% 8A-% E3% 82% A8% E3% 83% AA% E3% 83% BB% E3% 83% A9% E3% 83% B3% E3% 83% 80 You should be able to read% E3% 82% A6 / dp / 4000057200) (laughs)

Spin, quantum mechanics, and statistical mechanics are disciplines that discuss the micro world, and cannot be understood in a day or two. If you take this opportunity to study various things, you should be able to understand the fun and attention. (Originally, this book was number one in Amazon's physics category.)

* As an individual issue

-A rigorous overview of how the tunnel effect makes it easier to reach the optimal solution than traditional simulated annealing.

・ About Gibbs Sump Ring

I want to understand the above and write an article again (laughs)

Also, if you have any obvious mistakes or questions, please let us know. I will fix it.

I read "Quantum Computer Accelerates Artificial Intelligence" and tried to outline it in Python without using mathematical formulas.