[Introduction] I tried to implement it by myself while explaining to understand the binary tree

To understand the binary tree

What is a binary tree?

It is a kind of non-linear data structure having a tree structure.

Tree ADT does not consider the order of elements.

Every node in a binary tree has 0 to 2 children. Therefore, the root and the left subtree that expands to the left of the root and the right subtree that expands to the right can be generally visualized.

[Explanation of the binary tree by Wikipedia](https://ja.wikipedia.org/wiki/%E6%9C%A8%E6%A7%8B%E9%80%A0_(%E3%83%87%E3%) 83% BC% E3% 82% BF% E6% A7% 8B% E9% 80% A0))

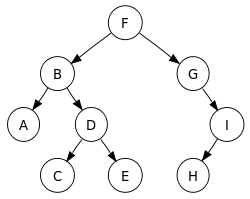
Purpose

• I want to deepen my understanding of data structures and algorithms by studying binary trees.
• Implement a binary tree data structure in python.
• Understand how-tos on how to handle binary tree data structures, not just implementing binary trees.
• Deep digging the basic binary tree to deepen the understanding of the binary search tree ⇒ Parent article

Contents

Data structure and node definition

• Node has a value (node.data)
• Have a connection to a child node (node.left = Node (data))
• The number of children is either 0, 1, or 2.
• The top node is the root node (self.root, ins.root)

Binary tree implementation

Creating a Node () object

Create a Node object and generate the following in the constructor. .Left and .right are also None because they have nothing to do with others at the time of generation

• Node value: self.data = data
• Link to child node of left subtree: self.left = None
• Link to child node of right subtree: self.right = None

Node_class.py

class Node:
    """ Node is user data structure　as binary tree  """
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

Binary tree generation

1. Create a Node object
2. Find the part where the child has no element and insert the Node.
3. There are multiple methods that traversal Node, considering the order of visits.

Points at the time of implementation

• Create a root node in the constructor.
• Introduce a function to insert a value in the constructor.
• The above implementation is defined after appearing as an instance method
• If you want to exit the method from within the while in the method, end it with return

binary_tree.py

class BinaryTree:
    """ user difine data structure BinaryTree """
    def __init__(self, arr):
        self.root = None #Create an empty root to serve as a basis for future processing

        for inserted_node_data in arr: #Process to insert the values of the nodes stored in the list sequentially
            print('....')
            print('try inserting ', inserted_node_data)
            self.insert(inserted_node_data)

    def insert(self, data):     #Insertion process (route generation ⇒ generate branch of each node) ・ ・ ・ The left branch has a value smaller than the current node
        if self.root == None:   #Because the root node is a special node that serves as the basis for tree analysis.Cases to be generated separately as root
            print('Root node is ....')
            self.root = Node(data) # Node()Create an instance and assign it
            print(self.root.data)

        else:
            level = 1
            flag = True
            next_queue = [self.root] #Create the first queue
            while flag:   #flag becomes False when all elements are None
                temp_queue, next_queue = next_queue, []
                level += 1

                for node in temp_queue:
                    #Left branch
                    #Add the currently node chiled node to the queue for the next operation
                    if node.left is not None:
                        next_queue.append(node.left)
                    #When None is found in child node, create a new node using data
                    else:
                        node.left = Node(data)
                        print('In level {}, {} is inseted'.format(level, data))
                        """
                        （AA）
After adding data to node, this insert ends
Here is for< while <Since it is in the insert method, use return to terminate the method in one shot
                        """
                        return 

                    #Right branch tree
                    #Add the currently node chiled node to the queue for the next operation
                    if node.right is not None:
                        next_queue.append(node.right)
                    #When None is found in child node, create a new node using data
                    else:
                        node.right = Node(data)
                        print('In level {}, {} is inseted'.format(level, data))
                        """
See (AA)
                        """
                        return

                flag = any(next_queue)

    ##########################
    #  Tree traversal
    ##########################
    def preoder_traversal(self, node, res):
        if node != None:
            print('queue', node.data)
            res.append(node.data)

            #Left subtree in preorder
            self.preoder_traversal(node.left, res)
            #Right subtree in preorder
            self.preoder_traversal(node.right, res)

        return res

    def inoder_traversal(self, node, res):
        if node != None:

            #Left subtree in order
            self.inoder_traversal(node.left, res)

            print('queue', node.data)
            res.append(node.data)

            #Right subtree in order
            self.inoder_traversal(node.right, res)
        return res

    def postorder_traversal(self, node, res):
        if node != None:
            self.postorder_traversal(node.left, res)
            self.postorder_traversal(node.right, res)
            print('queue', node.data)
            res.append(node.data)
        return res

    def level_order_traversal(self, queue, res= []):

        if queue == [] :
            # it's root
            print('root', self.root.data)
            res.append(self.root.data)
            queue.append(self.root)

        else:
            #Since the node of this level is a queue of arguments, turn it with for
            temp_list, queue = queue, []
            not_none_cnt = 0

            for item in temp_list:
                if item.left is not None:
                    res.append(item.left.data)
                    print('queue', item.left.data)
                    queue.append(item.left)
                    not_none_cnt += 1

                if item.right is not None:
                    res.append(item.right.data)
                    print('queue', item.right.data)
                    queue.append(item.right)
                    not_none_cnt += 1

            if not_none_cnt == 0:
                return #Go back to where you last called this function

        self.level_order_traversal(queue, res)

        return res

Binary tree method

Implemented methods to search for the maximum value, search for the presence or absence of a value, check the size, and check the height. See the comments in the code for points.

bt_method.py

#Binary tree method
class BT_method(BinaryTree):
    def __init__(self, arr):
        super().__init__(arr)

    def max_in_binary_tree(self, node, temp_max):
        """Implementation shows maximum value in parent-child relationship
It is the same even if you LIFO while travers and leave a large value.
Same thing as remembering the maximum value while traversing in a forward search"""
        if node is not None:
            temp_root_val = node.data
            left_val = self.max_in_binary_tree(node.left, temp_max)
            right_val = self.max_in_binary_tree(node.right, temp_max)

            temp_max = max(temp_root_val, left_val, right_val, temp_max)

        return temp_max

    def find_val(self, node, val, flag=False):
        if node != None:
            if node.data == val:
                return True

            else:
                flag_left = self.find_val(node.left, val) #Since the result of recursion is returned by return, it is received as a variable
                flag_right = self.find_val(node.right, val)

                if flag_left or flag_right:
                    return True

        return False


    def size(self, node):
        if node is None: #End counting when node is None
            return 0 #If you return 0, it will not be counted
        else:
            left_cnt = self.size(node.left)
            right_cnt = self.size(node.right)

            return 1 + left_cnt + right_cnt #I (not None) is 1 and the number in the left and right trees (virtual search is realized by a recursive function)


    def hight(self, level=0):
        flag = True
        queue = [self.root]

        while flag:
            level += 1
            temp_list, queue = queue, []
            for node in temp_list:
                if node.left is not None:
                    queue.append(node.left)
                if node.right is not None:
                    queue.append(node.right)


            flag = any(queue)

        return level

Run

I ran the code as below.

main.py

ins = BinaryTree(range(1,16))

print('--------------------------')
print('start preoder traversal')
print(ins.preoder_traversal(ins.root, []))

print('--------------------------')
print('start inoder traversal')
print(ins.inoder_traversal(ins.root, []))

print('--------------------------')
print('start postoder traversal')
print(ins.postorder_traversal(ins.root, []))

print('--------------------------')
print('start level order traversal')
print(ins.level_order_traversal([]))

#
print('=====================================')

ins2 = BT_method(range(1,16))
print('--------------------------')
print('find max')
print(ins2.max_in_binary_tree(ins2.root, 0))
print('--------------------------')
print('find value')
print('looking for 7', ins2.find_val(ins2.root, 7))
print('looking for 17', ins2.find_val(ins2.root, 17))


#  search size
print('--------------------------')
print('detect node size')
print(ins2.size(ins2.root))

Execution result

The print part tells us the behavior sequentially

....
try inserting  1
Root node is ....
1
....
try inserting  2
In level 2, 2 is inseted
....
try inserting  3
In level 2, 3 is inseted
....
try inserting  4
In level 3, 4 is inseted
....
try inserting  5
In level 3, 5 is inseted
....
try inserting  6
In level 3, 6 is inseted
....
try inserting  7
In level 3, 7 is inseted
....
try inserting  8
In level 4, 8 is inseted
....
try inserting  9
In level 4, 9 is inseted
....
try inserting  10
In level 4, 10 is inseted
....
try inserting  11
In level 4, 11 is inseted
....
try inserting  12
In level 4, 12 is inseted
....
try inserting  13
In level 4, 13 is inseted
....
try inserting  14
In level 4, 14 is inseted
....
try inserting  15
In level 4, 15 is inseted
--------------------------
start preoder traversal
queue 1
queue 2
queue 4
queue 8
queue 9
queue 5
queue 10
queue 11
queue 3
queue 6
queue 12
queue 13
queue 7
queue 14
queue 15
[1, 2, 4, 8, 9, 5, 10, 11, 3, 6, 12, 13, 7, 14, 15]
--------------------------
start inoder traversal
queue 8
queue 4
queue 9
queue 2
queue 10
queue 5
queue 11
queue 1
queue 12
queue 6
queue 13
queue 3
queue 14
queue 7
queue 15
[8, 4, 9, 2, 10, 5, 11, 1, 12, 6, 13, 3, 14, 7, 15]
--------------------------
start postoder traversal
queue 8
queue 9
queue 4
queue 10
queue 11
queue 5
queue 2
queue 12
queue 13
queue 6
queue 14
queue 15
queue 7
queue 3
queue 1
[8, 9, 4, 10, 11, 5, 2, 12, 13, 6, 14, 15, 7, 3, 1]
--------------------------
start level order traversal
root 1
queue 2
queue 3
queue 4
queue 5
queue 6
queue 7
queue 8
queue 9
queue 10
queue 11
queue 12
queue 13
queue 14
queue 15
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
=====================================
....
try inserting  1
Root node is ....
1
....
try inserting  2
In level 2, 2 is inseted
....
try inserting  3
In level 2, 3 is inseted
....
try inserting  4
In level 3, 4 is inseted
....
try inserting  5
In level 3, 5 is inseted
....
try inserting  6
In level 3, 6 is inseted
....
try inserting  7
In level 3, 7 is inseted
....
try inserting  8
In level 4, 8 is inseted
....
try inserting  9
In level 4, 9 is inseted
....
try inserting  10
In level 4, 10 is inseted
....
try inserting  11
In level 4, 11 is inseted
....
try inserting  12
In level 4, 12 is inseted
....
try inserting  13
In level 4, 13 is inseted
....
try inserting  14
In level 4, 14 is inseted
....
try inserting  15
In level 4, 15 is inseted
--------------------------
find max
15
--------------------------
find value
looking for 7 True
looking for 17 False
--------------------------
detect node size
15

References

• Introduction to Data Structures and Algorithms (O'Reilly)
• [Explanation of the binary tree by Wikipedia](https://ja.wikipedia.org/wiki/%E6%9C%A8%E6%A7%8B%E9%80%A0_(%E3%83%87%E3) % 83% BC% E3% 82% BF% E6% A7% 8B% E9% 80% A0))