Find the optimal cooking order

theme

Let's solve the Scheduling Problem by Professor Uno of the National Institute of Informatics.

Complete many processes (soup, yakitori, ...) as soon as possible using various resources (people, stoves, knives, ovens).

It can be formulated and solved with a general-purpose solver, but it is difficult, so use the scheduling solver OptSeq. There is a charge, but you can solve up to variable 15 with the free trial version.

See Scheduling Optimization Solver OptSeq II for installation and usage.

Solve with Python

Define an auxiliary function so that you do not have to specify the name one by one.

python

from more_itertools import pairwise
from optseq import *

def addResource(m, capacity=1, name=None, addResource_count=[0]):
    if name is None:
        addResource_count[0] += 1
        name = f'R{addResource_count[0]}'
    return m.addResource(name, capacity=capacity)
def addMode(dur, res=[], name=None, addMode_count=[0]):
    if name is None:
        addMode_count[0] += 1
        name = f'M{addMode_count[0]}'
    md = Mode(name, dur)
    for r in res:
        md.addResource(r, requirement=1)
    return md
def addActivity(m, dur, res=[], name=None, addActivity_count=[0]):
    if name is None:
        addActivity_count[0] += 1
        name = f'A{addActivity_count[0]}'
    ac = m.addActivity(name)
    md = addMode(dur, res)
    ac.addModes(md)
    return ac

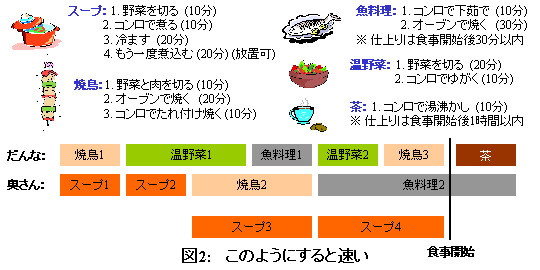
Let's actually make a model and solve it. The combinations of the four resources (person, stove, kitchen knife, oven) are 1,2,4,8 respectively so that they can be represented by one number. The 5 in "'Soup': [(5,10), ...]" means to use both 1 (person) and 4 (knife). 10 is the working time (minutes).

python

# 1:Man, 2:Stove, 4:Kitchen knife, 8:oven
prm = {'soup': [(5,10),(3,10),(0,20),(0,20)],
       'Yakitori': [(5,10),(9,20),(3,10)],
       'fish dishes': [(3,10),(9,30)],
       'Hot vegetables': [(5,20),(3,10)],
       'tea': [(3,10)]} #Resource flag,time
m = Model() #model
#resource
res = {i:addResource(m,j) for i,j in zip([1,2,4,8],[2,2,2,1])}
#Process
act = {k:[addActivity(m, d, [r for j,r in res.items() if f&j], f'{k}{i+1}')
        for i,(f,d) in enumerate(l)] for k,l in prm.items()}
for l in act.values():
    for i,j in pairwise(l):
        m.addTemporal(i,j) #In order within the same dish
m.addTemporal('sink',act['fish dishes'][1],'CC') # fish dishes2は最後に
m.addTemporal('sink',act['tea'][0],'CC') # tea1は最後に
m.Params.TimeLimit = 1 #Calculation time is up to 1 second
m.Params.Makespan = True #Minimize the end time of all processes
m.optimize() #Solver execution

result

 ================ Now solving the problem ================ 
Solutions:
    source     ---     0     0
      sink     ---    70    70
Soup 1---     0    10
Soup 2---    10    20
Soup 3---    20    40
Soup 4---    40    60
Yakitori 1---     0    10
Yakitori 2---    10    30
Yakitori 3---    30    40
Fish dish 1---    20    30
Fish dish 2---    40    70
Hot vegetables 1---    30    50
Hot vegetables 2---    50    60
Tea 1---    60    70

The two numbers represent the start and end times of the process. Since the sink is 70, we can see that the whole process is completed in 70 minutes. Also, even if you look at it individually, you can see that the answer is almost the same as the result of the teacher below.

that's all