J'ai rédigé un résumé de Cross Validation, de détermination d'hyperparamètres, de courbe ROC, AUC, etc., et une démonstration d'exécution en Python en relation avec le sobre mais important «évaluation / index du modèle».

Cet article est le 7ème jour du Calendrier de l'Avent Qiita Machine Learning 2015. Quand je l'ai regardé, 12/7 était gratuit, alors je l'ai écrit à la hâte: sourire:

Le code complet peut être trouvé dans le référentiel GitHub ici [https://github.com/matsuken92/Qiita_Contents/blob/master/Model_evaluation/Model_evaluation.ipynb).

0. Ensemble de données "Titanic"

Utilisez le jeu de données Titanic familier. Données sur les survivants du navire à passagers Titanic, souvent utilisées comme données de démonstration pour la classification.

Tout d'abord, le prétraitement et l'importation de données

J'ai un ensemble de données dans seaborn, donc je vais l'utiliser.

%matplotlib inline
import numpy as np
import pandas as pd
from time import time
from operator import itemgetter

import matplotlib as mpl
import matplotlib.pyplot as plt
from tabulate import tabulate
import seaborn as sns
sns.set(style="whitegrid", color_codes=True)

from sklearn import cross_validation
from sklearn import datasets
from sklearn import svm
from sklearn.ensemble import RandomForestClassifier
from sklearn.cross_validation import cross_val_score
from sklearn import grid_search

from sklearn.cross_validation import KFold
from sklearn.cross_validation import StratifiedKFold

from sklearn.metrics import classification_report, roc_auc_score, precision_recall_curve, auc, roc_curve

titanic = sns.load_dataset("titanic")

Ce sont les données. Les 5 premières lignes s'affichent.

headers = [c for c in titanic.columns]
headers.insert(0,"ID")
print tabulate(titanic[0:5], headers, tablefmt="pipe")

ID	survived	pclass	sex	age	sibsp	fare	embarked	class	who	adult_male	deck	embark_town	alive	alone
0	0	3	male	22	1	7.25	S	Third	man	1	nan	Southampton	no	0
1	1	1	female	38	1	71.2833	C	First	woman	0	C	Cherbourg	yes	0
2	1	3	female	26	0	7.925	S	Third	woman	0	nan	Southampton	yes	1
3	1	1	female	35	1	53.1	S	First	woman	0	C	Southampton	yes	0
4	0	3	male	35	0	8.05	S	Third	man	1	nan	Southampton	no	1

#Faire des variables catégoriques des variables factices
def convert_dummies(df, key):
    dum = pd.get_dummies(df[key])
    ks = dum.keys()
    print "Removing {} from {}...".format(ks[0], key)
    dum.columns = [key + "_" + str(k) for k in ks]  
    df = pd.concat((df, dum.ix[:,1:]), axis=1)
    df = df.drop(key, axis=1)
    return df

titanic = convert_dummies(titanic, "who")
titanic = convert_dummies(titanic, "class")
titanic = convert_dummies(titanic, "sex")
titanic = convert_dummies(titanic, "alone")
titanic = convert_dummies(titanic, "embark_town")
titanic = convert_dummies(titanic, "deck")
titanic = convert_dummies(titanic, "embarked")

titanic['age'] = titanic.age.fillna(titanic.age.median())
titanic['adult_male'] = titanic.adult_male.map( {True: 1, False: 0} ).astype(int)
titanic['alone'] = titanic.adult_male.map( {True: 1, False: 0} ).astype(int)

#Supprimer les variables inutilisées
titanic = titanic.drop("alive", axis=1)
titanic = titanic.drop("pclass", axis=1)

1. Division de l'ensemble de données

1-1. Méthode d'exclusion

Un certain pourcentage des données sur les enseignants dont nous disposons actuellement est divisé en «données de formation» et «données de test» pour l'apprentissage et l'évaluation. Par exemple, si le rapport entre les données d'entraînement et les données de test est de 80:20, cela ressemble à ceci.

#Données d'entraînement(80%),données de test(20%)Diviser en
target = titanic.ix[:, 0]
data = titanic.ix[:, [1,2,3,4,5,6,7,8,9,10,11,12,14]]
X_train, X_test, y_train, y_test = cross_validation.train_test_split(data, target, test_size=0.2, random_state=None)

print [d.shape for d in [X_train, X_test, y_train, y_test]]

`out`


[(712, 23), (179, 23), (712,), (179,)]

L'augmentation de la quantité de données d'entraînement augmente la précision de l'apprentissage, mais diminue la précision de l'évaluation du modèle.
L'augmentation de la quantité de données de test augmente la précision de l'évaluation du modèle mais diminue la précision de l'apprentissage.

Faites attention au compromis et décidez du ratio.

# SVM(Noyau linéaire)Classer et calculer le taux d'erreur
clf = svm.SVC(kernel='linear', C=1).fit(X_train, y_train)
print u"Taux d'erreur de réaffectation:", 1 - clf.score(X_train, y_train)   
print u"Taux d'erreur de maintien:", 1 - clf.score(X_test, y_test)

`out`


Taux d'erreur de réaffectation: 0.162921348315
Taux d'erreur de tenue: 0.212290502793

# SVM(noyau rbf)Classer et calculer le taux d'erreur
clf = svm.SVC(kernel='rbf', C=1).fit(X_train, y_train)
print u"Taux d'erreur de réaffectation:", 1 - clf.score(X_train, y_train)   
print u"Taux d'erreur de maintien:", 1 - clf.score(X_test, y_test)

`out`


Taux d'erreur de réaffectation: 0.101123595506
Taux d'erreur de tenue: 0.268156424581

1-2. Validation croisée (CV): pli k stratifié

K-fold Tout d'abord, à propos du simple pli en K. Prenons le cas où il y a 30 données. n_folds est le nombre de divisions, divise l'ensemble de données que vous avez maintenant par le nombre de divisions et génère toutes les combinaisons sous la forme d'une liste d'indices comme indiqué ci-dessous, qui sont les données de test.

 # KFold
# n_Divisez les données par la valeur numérique spécifiée par des plis. n_folds=S'il est 5, il est divisé en 5
#Ensuite, l'un d'eux est utilisé comme données de test et cinq modèles sont générés.
kf = KFold(30, n_folds=5,shuffle=False)
for tr, ts in kf:
    print("%s %s" % (tr, ts))

`out`


[ 6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29] [0 1 2 3 4 5]
[ 0  1  2  3  4  5 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29] [ 6  7  8  9 10 11]
[ 0  1  2  3  4  5  6  7  8  9 10 11 18 19 20 21 22 23 24 25 26 27 28 29] [12 13 14 15 16 17]
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 24 25 26 27 28 29] [18 19 20 21 22 23]
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] [24 25 26 27 28 29]

Stratified k-fold À partir du facteur K ci-dessus, une méthode de division de l'ensemble de données de manière à conserver chaque rapport de classe dans l'ensemble de données à portée de main. Le cross_validation.cross_val_score utilisé dans la section suivante l'adopte.

# StratifiedKFold
#Une version améliorée de KFold qui fait correspondre le taux d'extraction de chaque classe au rapport des données d'origine

label = np.r_[np.repeat(0,20), np.repeat(1,10)]
skf = StratifiedKFold(label, n_folds=5, shuffle=False)
for tr, ts in skf:
    print("%s %s" % (tr, ts))

`out`


[ 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 22 23 24 25 26 27 28 29] [ 0  1  2  3 20 21]
[ 0  1  2  3  8  9 10 11 12 13 14 15 16 17 18 19 20 21 24 25 26 27 28 29] [ 4  5  6  7 22 23]
[ 0  1  2  3  4  5  6  7 12 13 14 15 16 17 18 19 20 21 22 23 26 27 28 29] [ 8  9 10 11 24 25]
[ 0  1  2  3  4  5  6  7  8  9 10 11 16 17 18 19 20 21 22 23 24 25 28 29] [12 13 14 15 26 27]
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 20 21 22 23 24 25 26 27] [16 17 18 19 28 29]

Essayez de courir

# SVM(Noyau linéaire)Classer et calculer le taux d'erreur
#Calculez chaque score avec un pli en K stratifié divisé en 5

clf = svm.SVC(kernel='rbf', C=1)
scores = cross_validation.cross_val_score(clf, data, target, cv=5,)
print "scores: ", scores
print("Accuracy: %0.2f (+/- %0.2f)" % (scores.mean(), scores.std() * 2))

Puisque 5 est spécifié pour n_folds, 5 scores différents sont affichés. La précision est la valeur moyenne et l'écart type.

`out`


scores:  [ 0.67039106  0.70949721  0.74157303  0.74719101  0.78531073]
Accuracy: 0.73 (+/- 0.08)

2. Comment trouver de meilleurs hyper paramètres

2-1. Exhaustive Grid Search En d'autres termes, c'est un moyen d'essayer tous les hyperparamètres que vous avez définis à partir de zéro pour savoir lequel est le meilleur. Cela prendra du temps, mais nous essaierons tout ce que vous spécifiez pour que vous en trouviez probablement un bon.

Tout d'abord, définissez les valeurs possibles des paramètres comme suit.

param_grid = [
  {'kernel': ['rbf','linear'], 'C': np.linspace(0.1,2.0,20),}
 ]

Passez-le à grid_search.GridSearchCV avec SVC (Support Vector Classifier) et exécutez-le.

#Courir
svc = svm.SVC(random_state=None)
clf = grid_search.GridSearchCV(svc, param_grid)
res = clf.fit(X_train, y_train)

#Voir les résultats
print "score: ", clf.score(X_test, y_test)
print "best_params:", res.best_params_
print "best_estimator:", res.best_estimator_

Il essaie tous les paramètres spécifiés et affiche le score avec le meilleur résultat, quel paramètre était bon et le paramètre spécifié détaillé.

`out`


 0.787709497207
 {'kernel': 'linear', 'C': 0.40000000000000002}
 SVC(C=0.40000000000000002, cache_size=200, class_weight=None, coef0=0.0,
  degree=3, gamma=0.0, kernel='linear', max_iter=-1, probability=False,
  random_state=None, shrinking=True, tol=0.001, verbose=False)

Cependant, cela a pris du temps après tout. Lorsque le nombre de paramètres que vous souhaitez essayer augmente, vous ne pourrez pas tous les voir. Ensuite, je vais choisir une méthode qui incorpore le caractère aléatoire dans la façon de sélectionner les paramètres.

2-2. Randomized Parameter Optimization

Essayez d'augmenter les paramètres que vous souhaitez essayer. Cette fois, nous utiliserons Random forest, qui a de nombreux paramètres.

param_dist = {'n_estimators': range(4,20,2), 'min_samples_split': range(1,30,2), 'criterion':['gini','entropy']}

Exécutons-le et voyons combien de temps le temps de traitement est. (* Si le nombre de combinaisons de paramètres est inférieur ou égal à 20, une erreur apparaîtra indiquant "Utiliser la recherche par grille")

n_iter_search = 20
rfc = RandomForestClassifier(max_depth=None, min_samples_split=1, random_state=None)
random_search = grid_search.RandomizedSearchCV(rfc, 
                                   param_distributions=param_dist,
                                   n_iter=n_iter_search)
start = time()
random_search.fit(X_train, y_train)
end   = time()
print"Nombre de paramètres: {0},temps écoulé: {1:0.3f}Secondes".format(n_iter_search, end - start)

`out`


Nombre de paramètres: 20,temps écoulé: 0.805 secondes

Les 3 principaux réglages de paramètres sont indiqués ci-dessous.

#Top 3 des paramètres
top_scores = sorted(random_search.grid_scores_, key=itemgetter(1), reverse=True)[:3]
for i, score in enumerate(top_scores):
    print("Model with rank: {0}".format(i + 1))
    print("Mean validation score: {0:.3f} (std: {1:.3f})".format(
          score.mean_validation_score,
          np.std(score.cv_validation_scores)))
    print("Parameters: {0}".format(score.parameters))
    print("")

`out`


Model with rank: 1
Mean validation score: 0.834 (std: 0.007)
Parameters: {'min_samples_split': 7, 'n_estimators': 10, 'criterion': 'gini'}

Model with rank: 2
Mean validation score: 0.826 (std: 0.010)
Parameters: {'min_samples_split': 25, 'n_estimators': 18, 'criterion': 'entropy'}

Model with rank: 3
Mean validation score: 0.823 (std: 0.022)
Parameters: {'min_samples_split': 19, 'n_estimators': 12, 'criterion': 'gini'}

3. Indice d'évaluation

Considérez le résultat du diagnostic d'une certaine maladie comme exemple. À ce moment-là, il existe quatre résultats possibles, comme indiqué ci-dessous, en fonction du résultat du diagnostic et de la valeur réelle. Le tableau est le suivant.

De base,

T(true), F(false)
P(positive), N(negative)

En cas d'examen avec la combinaison de vrai signifie "le résultat du diagnostic et la valeur vraie correspondent", faux signifie "le résultat du diagnostic et la valeur vraie sont différents" Le positif est «malade», le négatif est «pas malade» Représente.

Sur cette base, les indices d'évaluation suivants sont calculés.

Taux de réponse correct [Précision]

{\rm Accuracy = { TP + TN \over TP + FP + FN + TN}}

Taux de précision [Précision]

Le pourcentage de réponses correctes parmi ceux dont le diagnostic est positif.

{\rm Precision = {TP \over TP + FP}}

Taux de rappel [Rappel]

Taux de réponse correct parmi ceux dont la vraie valeur est mauvaise

{\rm Recall = {TP \over TP + FN}}

Valeur F (mesure F)

Moyenne harmonisée de précision et de rappel.

{\rm F-measure = {2\cdot Precision \cdot Recall \over Precision +Recall }}

3-1. Essayez de calculer

# SVM(Noyau linéaire)Classer et calculer l'indice d'évaluation
clf = svm.SVC(kernel='linear', C=1, probability=True).fit(X_train, y_train)
print u"Accuracy:", clf.score(X_test, y_test)   
y_pred = clf.predict(X_test)
print classification_report(y_test, y_pred, target_names=["not Survived", "Survived"])

`out`


              precision    recall  f1-score   support

not Survived       0.80      0.86      0.83       107
    Survived       0.77      0.68      0.72        72

 avg / total       0.79      0.79      0.79       179

3-2. ROC et AUC

J'expliquerai l'index appelé AUC. Cela peut être dérivé de la courbe ROC (Receiver Operating Characteristic), mais dans l'article précédent,

[Statistiques] Comprenez ce qu'est la courbe ROC par animation.

Veuillez consulter ici pour des explications détaillées dans.

L'aire sous cette courbe ROC est AUC (Area Under the Curve). (C'est vrai ...: sweat_smile :)

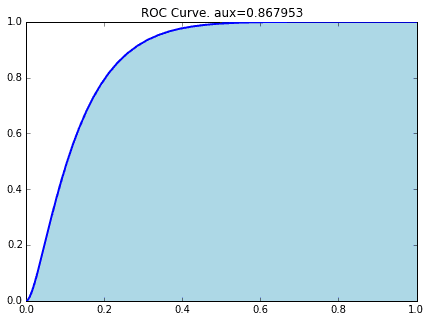
prob = clf.predict_proba(X_test)[:,1]
fpr, tpr, thresholds= roc_curve(y_test, prob)

plt.figure(figsize=(8,6))
plt.plot(fpr, tpr)
plt.title("ROC curve")
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.show()

La courbe ROC lorsque les données Titanic sont classées par SVM (Linear Kernel) est la suivante.

#Calcul de l'ASC
precision, recall, thresholds = precision_recall_curve(y_test, prob)
area = auc(recall, precision)
print "Area Under Curve: {0:.3f}".format(area)

`out`


Area Under Curve: 0.800

référence

WEB 　Scikit Learn User Guide 3. Model selection and evaluation 　　　http://scikit-learn.org/stable/model_selection.html

** Livres ** "Première reconnaissance de formes" Yuzo Hirai "Introduction à l'apprentissage automatique pour le traitement du langage" Manabu Okumura

[Apprentissage automatique] Résumé et exécution de l'évaluation / des indicateurs du modèle (avec jeu de données Titanic)

0. Ensemble de données "Titanic"

Tout d'abord, le prétraitement et l'importation de données

1. Division de l'ensemble de données

1-1. Méthode d'exclusion

out

out

out

1-2. Validation croisée (CV): pli k stratifié

out

out

Essayez de courir

out

2. Comment trouver de meilleurs hyper paramètres

out

out

out

3. Indice d'évaluation

Taux de réponse correct [Précision]

Taux de précision [Précision]

Taux de rappel [Rappel]

Valeur F (mesure F)

3-1. Essayez de calculer

out

3-2. ROC et AUC

out

référence

`out`

`out`

`out`

`out`

`out`

`out`

`out`

`out`

`out`

`out`

`out`