Méthode Ford-Falkerson et ses applications - Supplément au chapitre 8 de la référence rapide de l'algorithme -

Aperçu

Il s'agit d'une série de lecture de livres, de réétude de diverses choses et d'écriture de ce qui vous intéresse. Cette fois-ci, [Référence rapide de l'algorithme](http://www.amazon.co.jp/%E3%82%A2%E3%83%AB%E3%82%B4%E3%83%AA%E3%82% BA% E3% 83% A0% E3% 82% AF% E3% 82% A4% E3% 83% 83% E3% 82% AF% E3% 83% AA% E3% 83% 95% E3% 82% A1% E3% 83% AC% E3% 83% B3% E3% 82% B9-George-T-Heineman / dp / 4873114284) Le thème est "Algorithme de flux réseau" dans le chapitre 8. Dans l'ensemble, la méthode Ford-Falkerson est incroyable.

Partie principale 1: Aperçu de la méthode Ford-Falkerson

À propos de diverses quantités sur le graphique

(Dirigé) Nous pondérons souvent les arêtes sur le graphique. Le montant de ce poids est

――Temps et distance ――C'est le coût,

• Un certain débit

Cela correspond à divers concepts, mais tous sont formulés comme la même «pondération latérale».

Pour la méthode de prendre cette quantité de poids comme temps et distance et effectuer le calcul correspondant à "combien de temps il faudra entre un certain point de départ et le point de but", voir le Dikstra au chapitre 6. Je pense par la loi. Dans ce chapitre, nous examinerons les coûts et les débits mentionnés dans l'exemple ci-dessus.

Méthode Ford Falkerson et ses points

Tout d'abord, considérez débit = débit. Il existe une méthode bien connue sous le nom de méthode Ford Falkerson. Je pense que l'idée d'augmenter avidement la voie de l'augmentation est relativement facile à comprendre, mais je pense que le point important est de "penser au flux dans la direction opposée à la direction normale". Ici, je vais essayer d'expliquer en mettant l'accent sur cette idée. Par souci de clarté, considérez le graphique suivant, qui a un poids de 1 de chaque côté, et trouvez le débit maximum de S à T dans ce graphique. Dans ce graphique, il y a les trois routes suivantes de S à T, et toutes les routes sont épuisées uniquement par cette route. 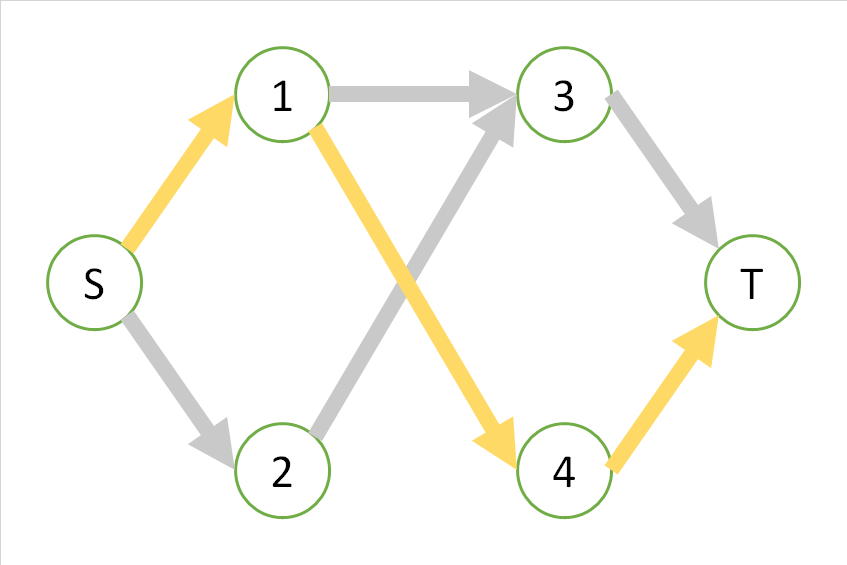Pour le moment, en regardant le premier itinéraire orange, cet itinéraire ne peut pas être utilisé en même temps que les itinéraires jaune et bleu. En ce sens, si vous prenez un chemin orange, vous ne pourrez plus augmenter le débit "en ajoutant plus de chemins parallèles au chemin orange", et le flux semble être "maximum". .. Par contre, puisque le chemin jaune et le chemin bleu peuvent être empruntés en même temps, même si seul le chemin jaune ou le chemin bleu est emprunté, ils ne sont pas "maximum", et le chemin qui prend le jaune et le bleu en même temps est "maximum". Il semble y avoir. Et dans ce cas, c'est aussi le débit maximum qui peut être prélevé en même temps. En général, un algorithme gourmand peut rester bloqué dans une valeur maximale appropriée, mais dans la méthode de Ford-Falkerson, cela est résolu en considérant le "flux incluant le sens inverse". En d'autres termes, nous pensons que les itinéraires suivants existent. Les côtés 3 à 1 n'existent pas dans le graphique d'origine, seuls les côtés 1 à 3 existent, donc les couleurs sont modifiées. Si vous écrivez le côté de 3 à 1 sous la forme $ e_ {31} $, ce sera $ e_ {31} = -e_ {13} $. Compte tenu de cet itinéraire également, l'itinéraire orange n'est plus le maximum, et le flux suivant peut être considéré. Les bords entre 1 et 3 sur cette figure s'annulent finalement et sont identiques à ne pas être utilisés. Si vous pensez à quelque chose comme "route imaginaire" comme le côté 3 à 1 de l'exemple actuel, vous n'avez pas à tomber dans une valeur maximale étrange. Cela dit, il n'est pas évident que cela ne correspond pas, alors je pense que c'est une affirmation surprenante. Bien que la preuve soit relativement facile.

Ce que j'ai dit jusqu'ici C'est aussi quelque chose comme ça. Et, selon la méthode Ford-Falkerson, cela signifie que peu importe laquelle des trois routes «existantes» est prise comme point de départ, le chemin croissant atteindra toujours le côté gauche ou droit de cette équation. je dis (Bien sûr, on dit que la même signification est vraie non seulement dans ce graphique, mais aussi dans les graphiques généraux.) C'est une propriété mathématique assez forte et je la trouve très intéressante. En fait, sur la façon d'emprunter ces itinéraires

• Si vous décidez de donner la priorité à la profondeur, la méthode originale de Ford Falkerson --Si vous décidez de donner la priorité à la largeur, la méthode Edmonds Carp
• Si vous décidez de hiérarchiser les coûts, la méthode double primale, qui est la solution au problème de flux de coût minimum

Vous pouvez obtenir un algorithme similaire. Derrière cela, comme nous l'avons vu ici, se trouve le fait que ** le débit maximum semble être une connexion linéaire (addition) des chemins ci-dessus **.

Pour expliquer la méthode Ford-Falkerson (généralisation) grosso modo en termes mathématiques,

――Clarifiez tous les itinéraires de S à T, y compris les itinéraires avec le sens de la flèche inversé. Dans le cas de cet exemple, $ e_ {s1} + e_ {13} + e_ {3t}, e_ {s2} + e_ {23} -e_ {13} + e_ {14} + e_ {4t}, e_ {s1} + e_ {14} + e_ {4t}, e_ {s2} + e_ {23} + e_ {3t} $ --Pour chacune de ces routes, définissez le débit sur 1 et créez l'équation suivante. Dans le cas de cet exemple $\\begin{align}+e_{s1}&&+e_{13}&&+e_{3t}&= 1 \\\\ &+e_{s2}+e_{23}&-e_{13}&+e_{14}+e_{4t}&&= 1 \\\\ +e_{s1}&&&+e_{14}+e_{4t}&&= 1 \\\\ &+e_{s2}+e_{23}&&&+e_{3t}&= 1 \\end{align}$

• Sous cette condition, je voudrais trouver la valeur maximale de la somme de ces connexions linéaires. La contrainte est $ 0 \ leq a_ {xy} \ leq $ (débit maximum de chaque côté), où le coefficient de $ e_ {xy} $ est $ a_ {xy} $.
• Afin de trouver réellement $ a_ {xy} $, ajoutez des équations qui satisfont les conditions de contrainte à une extrémité. ――La valeur maximale est atteinte quelle que soit la façon d'ajouter, mais la façon d'ajouter est modifiée en fonction de conditions telles que la vitesse de calcul et le coût.

Cela signifie que.

Partie principale 2: Implémentation du calcul du flux de coût minimum par Python

Problème de réglage

Maintenant, en plus des débits ci-dessus, des coûts peuvent être définis pour chaque côté. À ce stade, vous voudrez peut-être maintenir le coût aussi bas que possible tout en garantissant le débit de $ x $ de S à T. Par exemple, envisagez de traiter un article produit dans l'usine principale $ A $ dans l'usine secondaire $ B_1, B_2, B_3 $ et de le stocker dans le magasin $ C_1, C_2, C_3 $.

Plus précisément, supposez que vous disposez des débits et des coûts suivants:

• (Du sommet au sommet (débit, coût)) format

Les données

edges = {('A', 'B1', (100, 10)),
 ('A', 'B2', (100, 5)),
 ('A', 'B3', (100, 6)),
 ('B1', 'C1', (11, 5)),
 ('B1', 'C2', (10, 9)),
 ('B1', 'C3', (14, 5)),
 ('B2', 'C1', (17, 9)),
 ('B2', 'C2', (12, 6)),
 ('B2', 'C3', (20, 7)),
 ('B3', 'C1', (13, 7)),
 ('B3', 'C2', (11, 6)),
 ('B3', 'C3', (13, 10))}

Dans ces conditions, envisagez de faire passer le flux total de ** $ A $ 100 $ pour maintenir le coût aussi bas que possible **.

Réduire le problème de la synchronisation de source unique et ajouter des restrictions

En premier lieu, je vais modifier un peu le format du graphique pour indiquer clairement que la méthode Ford-Falkerson est un problème valide.

Ajouter un évier

C'est vraiment un problème formel, mais j'ajouterai le point $ D $ avant $ C_1, C_2, C_3 $. Cela correspond à T dans l'explication jusqu'à présent. L'arête de $ C_i $ à $ D $ est uniformément définie sur $ (100,0) $. Évidemment, cela n'a pas d'effet essentiel sur le problème.

Ajouter une source

Or, appliquer immédiatement la méthode Ford-Falkerson à ce problème donnerait un débit maximum simple, qui coûterait plus que le débit total de $ = 100 $. Donc, ajoutez le sommet $ A '$ avant $ A $. Le côté de $ A '$ à $ A $ est $ (100,0) $. Dans ces conditions, trouver le débit maximal correspond clairement à la limite de débit total de $ = 100 $ (en supposant que le débit maximal dans le graphique original dépasse 100 $). En fait, le débit maximum dans le graphique original est de 121 $, donc cette condition est bonne.

redessiner

résoudre

Je vais faire quelque chose qui peut être résolu pour le moment sans être conscient de la performance.

Les données

edges = {("A'", 'A', (100, 0)),
 ('A', 'B1', (100, 10)),('A', 'B2', (100, 5)),('A', 'B3', (100, 6)),
 ('B1', 'C1', (11, 5)),('B1', 'C2', (10, 9)),('B1', 'C3', (14, 5)),
 ('B2', 'C1', (17, 9)),('B2', 'C2', (12, 6)),('B2', 'C3', (20, 7)),
 ('B3', 'C1', (13, 7)),('B3', 'C2', (11, 6)),('B3', 'C3', (13, 10)),
 ('C1', 'D', (100, 0)),('C2', 'D', (100, 0)),('C3', 'D', (100, 0))}

definition.py

#Obtenez une liste de chemins ... Le résultat est une liste de coûts, une liste d'arêtes, une liste de coefficients
def getAllPath(edges, visited, f, t, r, c, e, a):
    if f == t:
        r.append((c,e,a))
    for k in neighbor[f].keys():
        if k not in visited:
            getAllPath(edges, visited + [f], k, t, r, c + neighbor[f][k][2], e + [neighbor[f][k][1]], a + [neighbor[f][k][0]])

#Renvoie "la valeur maximale que le chemin peut prendre maintenant" pour le chemin
def getMaximalFlow(world, (c,e,a)):
    l = len(e)
    delta = float("inf")
    for i in range(0, l):
        if a[i] > 0:
            if delta > world[e[i]][0] - world[e[i]][1]:
                delta = world[e[i]][0] - world[e[i]][1]
        elif a[i] < 0:
            if delta > world[e[i]][1]:
                delta = world[e[i]][1]
        else:
            delta = 0
    return delta

#Mettre à jour le graphique
def updateWorld(world, (c,e,a), delta):
    l = len(e)
    for i in range(0, l):
        world[e[i]] = (world[e[i]][0], world[e[i]][1] + a[i] * delta)

Les noms des variables sont plutôt bons. Au fait, bien que les fichiers soient séparés, ils sont en fait exécutés dans un autre bloc du notebook ipython (jupyter). (Autrement dit, les variables, etc. sont héritées)

solve.py

neighbor = {}
world = {}
for (f,t,(v,c)) in edges:
    #Dictionnaire des coûts
    if not f in neighbor.keys():
        neighbor[f] = {}
    neighbor[f][t] = (1,(f,t),c) #Facteur de pondération, base, coût
    if not t in neighbor.keys():
        neighbor[t] = {}
    neighbor[t][f] = (-1,(f,t),-c) #Facteur de pondération, base, coût
    #Dictionnaire pour stocker la valeur actuelle
    world[(f,t)] = (v,0) #Valeur maximale, valeur actuelle

r = []
getAllPath(edges,[],"A'",'D',r,0,[],[])
r.sort()

l = len(r)
i = 0
while i < l:
    delta = getMaximalFlow(world, r[i])
    if delta > 0:
        updateWorld(world, r[i], delta)
        i = 0
    else:
        i = i + 1

world

résultat

{('A', 'B1'): (100, 25), ('A', 'B2'): (100, 49), ('A', 'B3'): (100, 26),
 ("A'", 'A'): (100, 100),
 ('B1', 'C1'): (11, 11), ('B1', 'C2'): (10, 0), ('B1', 'C3'): (14, 14),
 ('B2', 'C1'): (17, 17), ('B2', 'C2'): (12, 12), ('B2', 'C3'): (20, 20),
 ('B3', 'C1'): (13, 13), ('B3', 'C2'): (11, 11), ('B3', 'C3'): (13, 2),
 ('C1', 'D'): (100, 41), ('C2', 'D'): (100, 23), ('C3', 'D'): (100, 36)}

Cela peut être un peu déroutant. Il ressemble à ceci lorsqu'il est visualisé. Bien qu'il soit partiellement coupé.

En tant que méthode de vérification simple, $ B_3 \ à C_3 $ est $ 2/13 $ et $ B_1 \ à C_2 $ est $ 0/10 $, mais c'est une route très coûteuse, donc le calcul lui-même est Ça rentre. Si vous voulez évaluer la vitesse, je pense que vous devriez la comparer avec Solver que Python (Networkx) a, mais comme il s'agit essentiellement d'étudier, la comparaison est inférieure.

Autres suppléments

Points concernant le retour

"Ajouter des points et des arêtes qui ne sont pas dans le graphe courant" est une pratique courante utilisée pour réduire à un autre problème en relation avec le graphe. C'est facile à comprendre, comme la conversion d'un graphe non orienté en graphe orienté, l'ajout d'un nouveau nœud et d'une arête au début, l'ajout d'un nouveau nœud et d'une arête à la fin, etc. Il existe d'autres méthodes telles que la division du nœud en deux. (Dans ce cas, je pense que $ A` $ ressemble plus à la division de nœuds qu'à l'ajout de nouveaux points.)

Code de dessin

drawGraphy.py

#Visualisation
import networkx as nx
import matplotlib.pyplot as plt
import math

G = nx.DiGraph()
srcs, dests = zip(* [(fr, to) for (fr, to) in world.keys()])
G.add_nodes_from(srcs + dests)

for (s,r,(d,c)) in edges:
    G.add_edge(s, r, weight=20/math.sqrt(d))

#Position, affiner
pos = {"A'"  : ([-0.55,0]),
       'A'  : ([0.25,0]),
       'B1' : ([1,-1.2]),
       'B2' : ([1,0]),
       'B3' : ([1,1.2]),
       'C1' : ([2,-1.2]),
       'C2' : ([2,0]),
       'C3' : ([2,1.2]),
       'D' : ([2.8,0]),
      }

edge_labels=dict([((f,t,),str(world[(f,t)][1]) + '/' + str(world[(f,t)][0]) )
             for (f,t) in world.keys()]) #Changer l'étiquette latérale de manière appropriée

plt.figure(1)
nx.draw_networkx(G, pos, with_labels=True)
nx.draw_networkx_edge_labels(G,pos,edge_labels=edge_labels,label_pos=0.74) #Ceci est également ajusté de manière appropriée

plt.axis('equal')
plt.show()

La fin

Vient ensuite A *. Le chapitre 7 est également Python. À propos, il existe d'autres articles de cette série comme suit. Bucket sort and n log n wall-Supplement to Chapter 4 of Algorithm Quick Reference- * Ruby Division de la recherche et du calcul - Supplément au chapitre 5 de la référence rapide de l'algorithme- * Python Résoudre le labyrinthe avec Python-Supplément au chapitre 6 de la Référence rapide de l'algorithme- * Python [Cet article →] Méthode Ford-Falkerson et son application - Supplément au chapitre 8 de la référence rapide de l'algorithme- * Python