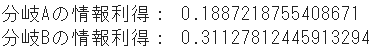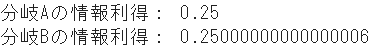- Il existe plusieurs critères de classification pour l'arbre de décision.
- On utilise couramment deux mesures d'impuretés, les impuretés Gini et l'entropie, et un critère de division appelé erreur de classification erronée.
- Voyons ces différences.
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
Comparaison de chaque indice en 2 classes de classification
- Dans la classification à 2 classes, si le rapport d'une classe est p, chaque indice est calculé comme suit.
- ** Gini: 2 p $ * (1 p) $ **
- ** entropie: $ -p * \ log p- (1-p) * log (1-p) $ **
- ** taux d'erreur de classification: 1 $ max (p, 1 p) $ **
#Générer une séquence d'égalité correspondant à p
xx = np.linspace(0, 1, 50) #Valeur de départ 0, valeur de fin 1, nombre d'éléments 50
plt.figure(figsize=(10, 8))
#Calculer chaque indice
gini = [2 * x * (1-x) for x in xx]
entropy = [-x * np.log2(x) - (1-x) * np.log2(1-x) for x in xx]
misclass = [1 - max(x, 1-x) for x in xx]
#Afficher le graphique
plt.plot(xx, gini, label='gini', lw=3, color='b')
plt.plot(xx, entropy, label='entropy', lw=3, color='r')
plt.plot(xx, misclass, label='misclass', lw=3, color='g')
plt.xlabel('p', fontsize=15)
plt.ylabel('criterion', fontsize=15)
plt.legend(fontsize=15)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.grid()
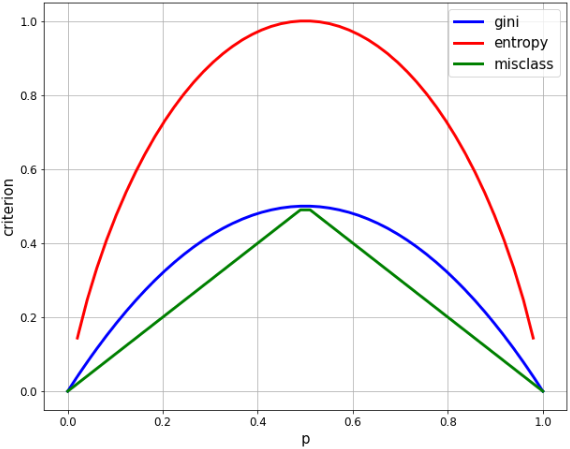
- Lorsque le rapport de 2 classes est égal (p = 0,5), les deux sont les valeurs maximales,
- L'entropie maximale est de 1,0 et le gini est de 0,5, donc mettez à l'échelle l'entropie d'un facteur 1/2 pour une comparaison facile.
#Générer une séquence d'égalité correspondant à p
xx = np.linspace(0, 1, 50) #Valeur de départ 0, valeur de fin 1, nombre d'éléments 50
plt.figure(figsize=(10, 8))
#Calculer chaque indice
gini = [2 * x * (1-x) for x in xx]
entropy = [(x * np.log((1-x)/x) - np.log(1-x)) / (np.log(2)) for x in xx]
entropy_scaled = [(x * np.log((1-x)/x) - np.log(1-x)) / (2*np.log(2)) for x in xx]
misclass = [1 - max(x, 1-x) for x in xx]
#Afficher le graphique
plt.plot(xx, gini, label='gini', lw=3, color='b')
plt.plot(xx, entropy, label='entropy', lw=3, color='r', linestyle='dashed')
plt.plot(xx, entropy_scaled, label='entropy(scaled)', lw=3, color='r')
plt.plot(xx, misclass, label='misclass', lw=3, color='g')
plt.xlabel('p', fontsize=15)
plt.ylabel('criterion', fontsize=15)
plt.legend(fontsize=15)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.grid()
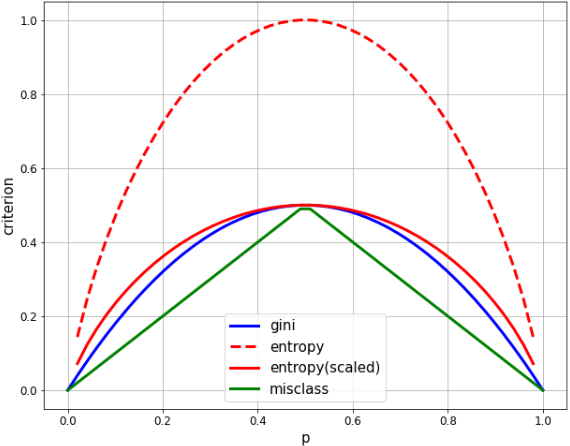
- Gini et l'entropie sont très similaires, tous deux dessinant une courbe quadratique et maximisant à p = 1/2.
- La classification erronée est clairement différente en ce qu'elle est linéaire, mais partage plusieurs des mêmes caractéristiques. Il maximise à p = 1/2, égale zéro à p = 0, 1 et change dans une montagne.
Différences dans chaque indice de gain d'information
1. Qu'est-ce que le gain d'information?
- ** gain d'information ** est un indice qui montre à quel point l'impureté est réduite avant et après ** la division lorsque les données sont divisées à l'aide d'une certaine variable.
- Moins elle est impure, plus la variable est utile comme condition de classification.
- En ce sens, réduire la pureté est synonyme de ** maximiser le gain d'information à chaque succursale **.
- Pour la classification à deux classes, le ** gain d'information (IG) ** est défini dans la formule suivante.
- \displaystyle IG(D_{p}, a) = I(D_{p}) - \frac{N_{left}}{N} I(D_{left}) - \frac{N_{right}}{N} I(D_{right})
- $ I $ signifie impur, $ D_ {p} $ est les données du nœud parent, la gauche et la droite des données du nœud enfant sont $ D_ {gauche} $ et $ D_ {droite} $, et le parent Les rapports gauche et droit des nœuds enfants sont basés sur le nombre d'échantillons de nœuds $ N $ comme dénominateur.
2. Calculez le gain d'information pour chaque indice
- Supposons les deux conditions de branchement suivantes A et B.
- Comparez le gain d'informations entre les conditions de branchement A et B pour chacun des taux de Gini, d'entropie et de mauvaise classification.
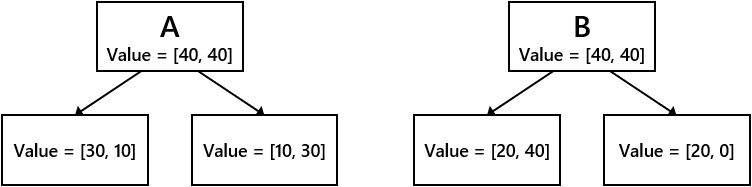
➀ Gain d'information dû à Gini impur
#Pureté Gini du nœud parent
IGg_p = 2 * 1/2 * (1-(1/2))
#Impureté de Gini du nœud enfant A
IGg_A_l = 2 * 3/4 * (1-(3/4)) #la gauche
IGg_A_r = 2 * 1/4 * (1-(1/4)) #droite
#Impureté de Gini du nœud enfant B
IGg_B_l = 2 * 2/6 * (1-(2/6)) #la gauche
IGg_B_r = 2 * 2/2 * (1-(2/2)) #droite
#Gain d'information de chaque agence
IG_gini_A = IGg_p - 4/8 * IGg_A_l - 4/8 * IGg_A_r
IG_gini_B = IGg_p - 6/8 * IGg_B_l - 2/8 * IGg_B_r
print("Gain d'information de la branche A:", IG_gini_A)
print("Gain d'information de la branche B:", IG_gini_B)

➁ Gain d'information de l'entropie
#Entropie du nœud parent
IGe_p = (4/8 * np.log((1-4/8)/(4/8)) - np.log(1-4/8)) / (np.log(2))
#Entropie du nœud enfant A
IGe_A_l = (3/4 * np.log((1-3/4)/(3/4)) - np.log(1-3/4)) / (np.log(2)) #la gauche
IGe_A_r = (1/4 * np.log((1-1/4)/(1/4)) - np.log(1-1/4)) / (np.log(2)) #droite
#Entropie du nœud enfant B
IGe_B_l = (2/6 * np.log((1-2/6)/(2/6)) - np.log(1-2/6)) / (np.log(2)) #la gauche
IGe_B_r = (2/2 * np.log((1-2/2+1e-7)/(2/2)) - np.log(1-2/2+1e-7)) / (np.log(2)) #droite,+1e-7 ajoute une petite valeur pour éviter 0 division
#Gain d'information de chaque agence
IG_entropy_A = IGe_p - 4/8 * IGe_A_l - 4/8 * IGe_A_r
IG_entropy_B = IGe_p - 6/8 * IGe_B_l - 2/8 * IGe_B_r
print("Gain d'information de la branche A:", IG_entropy_A)
print("Gain d'information de la branche B:", IG_entropy_B)
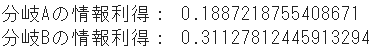
➂ Gain d'informations en raison du taux d'erreurs de classification
#Taux d'erreur de classification du nœud parent
IGm_p = 1 - np.maximum(4/8, 1-4/8)
#Taux d'erreur de classification du nœud enfant A
IGm_A_l = 1 - np.maximum(3/4, 1-3/4) #la gauche
IGm_A_r = 1 - np.maximum(1/4, 1-1/4) #droite
#Taux d'erreur de classification du nœud enfant B
IGm_B_l = 1 - np.maximum(2/6, 1-2/6) #la gauche
IGm_B_r = 1 - np.maximum(2/2, 1-2/2) #droite
#Gain d'information de chaque agence
IG_misclass_A = IGm_p - 4/8 * IGm_A_l - 4/8 * IGm_A_r
IG_misclass_B = IGm_p - 6/8 * IGm_B_l - 2/8 * IGm_B_r
print("Gain d'information de la branche A:", IG_misclass_A)
print("Gain d'information de la branche B:", IG_misclass_B)
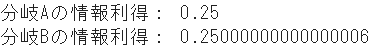
Résumé
|
Condition de classification A |
Condition de classification B |
| Gini Impure |
0.125 |
0.167 |
| Entropie |
0.189 |
0.311 |
| Taux d'erreurs de classification |
0.250 |
0.250 |
- Il est clair que la condition de classification B est prioritaire à la fois dans Gini et Entropy. En fait, les résultats seront très similaires.
- Par contre, dans le taux d'erreurs de classification, les conditions de classification A et B sont presque les mêmes.
- De cette façon, le taux d'erreurs de classification a tendance à ne pas prendre une différence claire entre les variables, donc dans le modèle d'arbre de décision de sklearn, il y a deux critères de division (semble-t-il): gini et entropie.
- De plus, Gini peut être un peu plus rapide car il n'y a pas de calcul logarithmique comme l'entropie.