[Python] Mes prévisions de cours de bourse [HFT]
1. Motivation
- Il existe divers articles sur les prévisions de cours boursiers même si vous regardez l'article de Qiita, mais dans cet article, j'ai décidé d'essayer sérieusement de prévoir les cours boursiers.
- La prévision du cours de l'action ici est une ** prévision à court terme ** qui est à quelques minutes.
- ** Lorsque vous regardez le tableau de la bourse, vous pouvez avoir l'impression que l'achat est fort ou que la vente est élevée, mais cette approche consiste à prédire le cours de l'action en fonction de cela.
- Je me suis référé à l'article "Deep Convolutional Neural Networks for Limit Order Books". Limit Order Book (LOB) signifie des informations sur la carte.
- En outre, l'ensemble de données utilise des données de la Bourse d'Helsinki en Finlande appelée FI-2010.
2. À propos des informations sur la carte
- Pour plus d'informations sur le forum, l'article Zai Online explique d'une manière facile à comprendre. En termes simples, un tableau est un ensemble des besoins de vente et d'achat suivants. Les ordres d'achat et de vente de diverses personnes sont rassemblés en bourse. ●● Les ordres tels que la volonté d'acheter (vendre) XX actions en yens sont agrégés par prix et le nombre total d'actions est affiché.
| Quantité de vente(ASK) | Prix de l'action | Acheter la quantité(BID) |
|---|---|---|
| 500 | 670 | |
| 400 | 669 | |
| 600 | 668 | |
| 667 | 300 | |
| 666 | 1,200 | |
| 665 | 400 |
- Il existe différentes façons de penser pourquoi et comment le cours de l'action fluctue, mais ici, nous pensons que si la quantité vendue des personnes qui veulent acheter est supérieure à la quantité vendue des personnes qui veulent vendre, le prix de l'action augmentera.
- Dans l'exemple du tableau ci-dessus, considérons le cas où une personne souhaitant acheter 100 actions apparaît et passe une nouvelle commande. Il existe à peu près deux modèles de commande.
- La première méthode consiste à passer votre propre ordre d'achat même s'il existe un ordre de vente de 600 actions pour 668 yens. À ce stade, la carte change comme indiqué ci-dessous.
| ASK | Prix de l'action | BID |
|---|---|---|
| 500 | 670 | |
| 400 | 669 | |
| 500 | 668 | |
| 667 | 300 | |
| 666 | 1,200 | |
| 665 | 400 |
- L'autre est de passer un ordre d'achat pour 667 yens, par exemple. Ce n'est pas toujours un contrat, mais un achat sera réalisé lorsqu'un ordre de vente sortira à 667 yens. À ce stade, la carte change comme indiqué ci-dessous.
| ASK | Prix de l'action | BID |
|---|---|---|
| 500 | 670 | |
| 400 | 669 | |
| 600 | 668 | |
| 667 | 400 | |
| 666 | 1,200 | |
| 665 | 400 |
- Ce que je veux dire ici est le suivant.
- Lorsque le nombre de personnes qui veulent acheter augmente, les informations du tableau seront une réaction que ** la quantité de DEMANDE diminue ou la quantité de BID augmente **.
- Lorsque le nombre de personnes qui veulent vendre augmente, les informations du tableau seront une réaction que ** la quantité de DEMANDE augmente ou la quantité de BID diminue **.
- ** Pensez-vous que si vous suivez attentivement les informations du conseil, vous pouvez obtenir des suggestions sur la transition ultérieure du cours des actions **? ??
3. Ensemble de données FI-2010
Qu'est-ce que le jeu de données FI-2010?
- Il y a une explication détaillée dans le document Benchmark Dataset for Mid-Price Forecasting of Limit Order Book Data with Machine Learning Methods, et ce qui suit en est un extrait.
- Données d'information sur le conseil tirées de la bourse d'Helsinki en Finlande.
- Données pour la période du 1er au 14 juin 2010.
- Les actions cibles sont 5 actions. Kesco (KESBV), Out Kumpu (OUT1V), Sampo Konzern (SAMPO), Rotor Rookie (RTRKS), Balchira (WET1V). Je ne connaissais pas toutes les marques.
- Il semble que les données soient échantillonnées à chaque fois qu'il y a un changement dans la carte. (Je pense que le nombre de données est petit pour cela, donc ma compréhension peut être différente ici. Cependant, je ne sais pas car nous sommes en 2010.)
- Vous pouvez télécharger les données normalisées. Les trois types de normalisation suivants sont disponibles.
- Z-score
\quad x_i^{Zscore} = \frac{x_i - x_{mean}}{x_{std}} \quad \rm where \quad x_{mean} = \frac{1}{N} \sum_{j=1}^{N} x_j, \quad x_{std} = \sqrt{\frac{1}{N} \sum_{j=1}^{N} (x_j - x_{mean})^2} - Min-Max Scaling
\quad x_i^{(MM)} = \frac{x_i - x_{min}}{x_{max} - x_{min}} - Decimal Precision
\quad x_i^{DP} = \frac{x_i}{10^k} \quad where k is the integer that will give the maximum value for|x_i^{(DP)}|<1 - Cliquez sur le lien ici (https://etsin.avointiede.fi/dataset/urn-nbn-fi-csc-kata20170601153214969115) Disponibilité des données Accédez gratuitement à cet ensemble de données Pour le télécharger.
Aperçu des données
- Ci-dessous, nous examinerons les données normalisées par la précision décimale. C'est parce que je pense que les chiffres dans les données sont les plus faciles à comprendre intuitivement. Tout d'abord, vous pouvez lire les données du premier jour sur les 10 jours de données.
data = pd.read_csv('Train_Dst_Auction_DecPre_CF_1.txt',
header=None, delim_whitespace=True)
print(data.shape)
#=> (149, 47342)
- Il y a 47 342 données au total, et vous pouvez voir que chacune est composée de 149 éléments.
- Il est difficile de saisir l'image dans son ensemble, alors regardons la carte thermique.
plt.figure(figsize=(20,10))
plt.imshow(data, interpolation='nearest', vmin=0, vmax=0.75,
cmap='jet', aspect=data.shape[1]/data.shape[0])
plt.colorbar()
plt.grid(False)
plt.show()
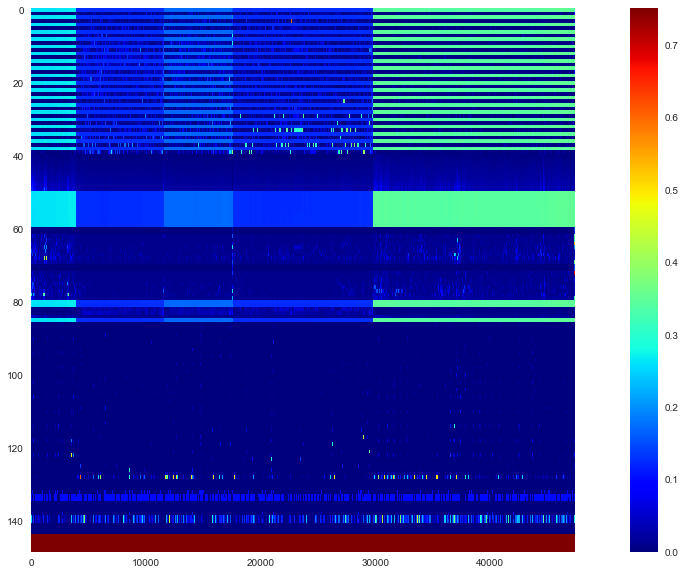
- Si vous regardez cela, vous pouvez voir que les données de 5 marques sont connectées côte à côte. Les 144 lignes du haut représentent les entités et les 5 dernières lignes représentent les étiquettes. En outre, il y a la description suivante dans l'article sur la quantité de caractéristiques spécifiques.

- Les informations de base sur le tableau sont en 40 lignes de $ u_1 $. Après cela, il s'agit d'une quantité de caractéristiques créée par le traitement des informations de la carte. Examinons de plus près comment les données sont contenues dans les informations du tableau. Utilisez la première colonne comme un essai.
lob = data.iloc[:40,0].values
lob_df = pd.DataFrame(lob.reshape(10,4),
columns=['ask','ask_vol','bid','bid_vol'])
print(lob_df)
| ask | ask_vol | bid | bid_vol | |
|---|---|---|---|---|
| 0 | 0.2631 | 0.00392 | 0.2616 | 0.00663 |
| 1 | 0.2643 | 0.00028 | 0.2615 | 0.00500 |
| 2 | 0.2663 | 0.00165 | 0.2614 | 0.00500 |
| 3 | 0.2664 | 0.00500 | 0.2613 | 0.00043 |
| 4 | 0.2667 | 0.00039 | 0.2612 | 0.00646 |
| 5 | 0.2710 | 0.00700 | 0.2611 | 0.00200 |
| 6 | 0.2745 | 0.00200 | 0.2609 | 0.00199 |
| 7 | 0.2749 | 0.00487 | 0.2602 | 0.00081 |
| 8 | 0.2750 | 0.00300 | 0.2600 | 0.00197 |
| 9 | 0.2769 | 0.01000 | 0.2581 | 0.01321 |
- C'est facile à comprendre lorsque vous venez ici. Les meilleurs ASK et BID sont en haut, et les informations du tableau deviennent progressivement loin du meilleur signe.
$ \ quad u_1 = \ {P_i ^ {ask}, V_i ^ {ask}, P_i ^ {bid}, V_i ^ {bid} \} _ {i = 1} ^ {10} $
Comme décrit dans>, les données en 40 lignes se présentent sous la forme "1er (meilleur) prix DEMANDER, quantité DEMANDER, prix BID, quantité BID, 2ème prix DEMANDER, quantité DEMANDER, prix BID, quantité BID ..." Il est stocké au format.
4. Modèle
Données de formation et étiquettes
- À partir de là, nous expliquerons le modèle d'apprentissage automatique qui est réellement utilisé. Les données d'apprentissage $ \ mathbb X $ et l'étiquette correspondante $ \ mathbb y $ sont nécessaires pour l'entraînement, mais c'est environ $ (\ mathbb x_t, y_t) $ qui compose cela.
- ** Données utilisées pour l'apprentissage **, mais à un moment donné $ t $ données de la carte
$ \ quad v_t = \ {P_ {t, i} ^ {ask}, V_ {t, i} ^ {ask}, P_ {t, i} ^ {bid}, V_ {t, i} ^ {bid} \} _ {i = 1} ^ {10} $
et voici le dernier $ p Une donnée d'apprentissage ($ \ mathbb x \ _t $) est obtenue en collectant $ pièces. Plus précisément,
$ \ quad \ mathbb x \ _t = \ begin {pmatrix} v \ _ {t-p + 1} \\ v \ _ {t-p + 2} \\ \ vdots \\ v \ _t \ end {pmatrix} = \ begin {pmatrix} P \ _ {t-p + 1,1} ^ {demander} & V \ _ {t-p + 1,1} ^ {demander} & P \ _ {t-p + 1,1} ^ {bid} & V \ _ {t-p + 1,1} ^ {bid} & P \ _ {t-p + 1,2} ^ {ask } & \ cdots & P \ _ {t-p + 1,10} ^ {bid} & V \ _ {t-p + 1,10} ^ {bid} \\ P \ _ {t-p + 2 , 1} ^ {demander} & V \ _ {t-p + 2,1} ^ {demander} & P \ _ {t-p + 2,1} ^ {bid} & V \ _ {t-p + 2,1} ^ {bid} & P \ _ {t-p + 2,2} ^ {ask} & \ cdots & P \ _ {t-p + 2,10} ^ {bid} & V \ _ { t-p + 2,10} ^ {bid} \\ \ vdots & \ vdots & \ vdots & \ vdots & \ vdots & \ ddots & \ vdots & \ vdots \\ P \ _ {t, 1} ^ {ask} & V \ _ {t, 1} ^ {ask} & P \ _ {t, 1} ^ {bid} & V \ _ {t, 1} ^ {bid} & P \ _ {t, 2 } ^ {ask} & \ cdots & P \ _ {t, 10} ^ {bid} & V \ _ {t, 10} ^ {bid} \ end {pmatrix} $
$ p × 40 $ Ce sera une file d'attente. Après la convolution avec CNN, elles sont passées par LSTM, de sorte que les données les plus anciennes se trouvent sur la première ligne et les données à $ t $ sont sur la ligne du bas. - ** L'étiquette ** ($ y_t $) indique si le prix médian moyen de la période $ k $ après $ t $ augmente, diminue ou se stabilise en fonction du seuil $ \ alpha
. Allouer à et. Premièrement, le point médian ( p_t $) est la moyenne des meilleurs ASK et BID à chaque instant, donc
$ \ quad p_t = \ frac {P_ {t, 1} ^ {ask} + P_ { Il devient t, 1} ^ {bid}} {2} $
. De plus, la valeur moyenne ($ m_ {+} (t) $) du prix médian dans la période $ k $ et son taux d'augmentation / diminution ($ l_t $) sont
$ \ quad m_ {+} (t) = \ frac. {1} {k} \ sum_ {i = 1} ^ {k} p_ {t + i}, \ quad l_t = \ frac {m_ {+} (t) --p_t} {p_t} $
peut faire. Enfin, en fonction du seuil ($ \ alpha $),
$ \ quad y_t = \ left \ {\ begin {array} {} 1, & l_t> \ alpha \\ -1, & l_t < - \ alpha \\ 0, & \ rm sinon \ end {array} \ right. $
Libellez-le
Architecture modèle
- Ce qui suit est un exemple du modèle en premier. Tout d'abord, les informations de la carte à chaque instant sont pliées par CNN, et enfin, la relation de série chronologique est traitée par LSTM.
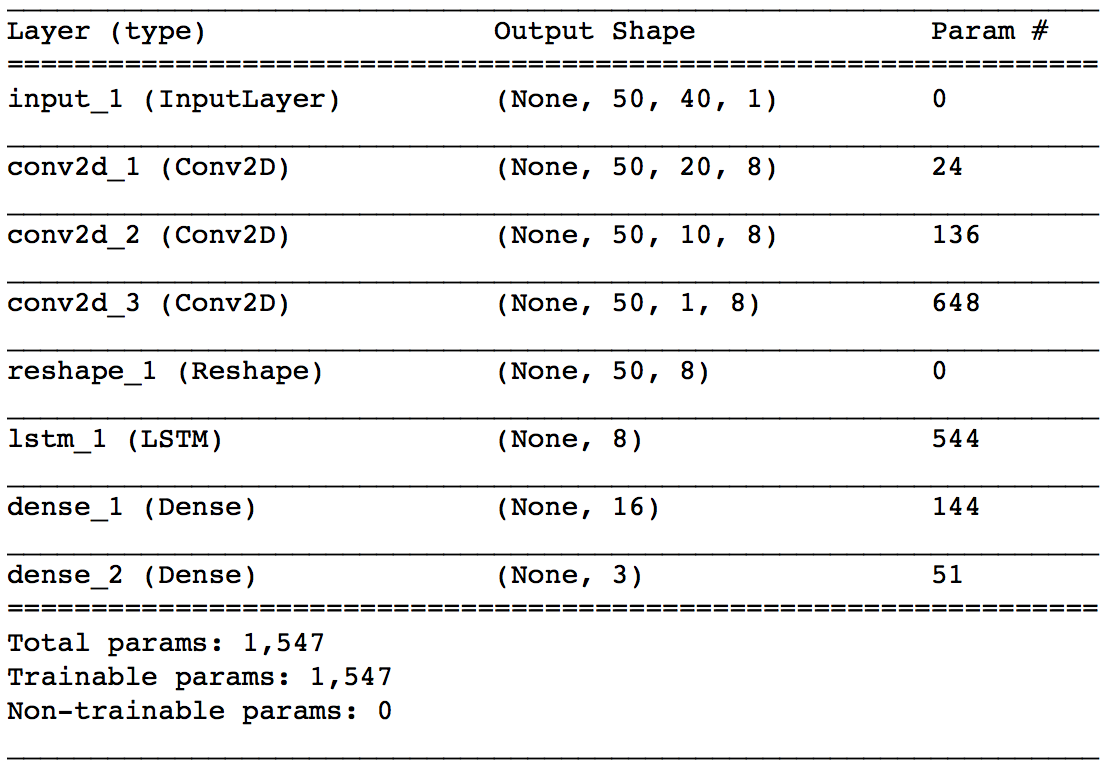
- ** input_1 ** Commençons par les couches. La forme de sortie signifie (taille du lot, nombre d'informations de carte auxquelles se référer ($ p $), nombre de données incluses dans une information de carte (40), 1). Ici, $ p = 50 $.
- ** conv2d_1 ** La couche est la première couche de convolution. La taille du noyau est de 1 $ x 2 $ et la foulée est de 1 $ x 2 $. Les paires de prix et de quantité d'informations sur la carte sont listées dans $ \ mathbb x_t $, mais ici nous convoluons chaque paire. Le nombre de noyaux est spécifié comme 8. Ici, seul le pliage dans le sens de la rangée est effectué, de sorte que le nombre d'informations de carte référencées par Output Shape reste inchangé à $ p (= 50) $, et le nombre de données contenues dans une information de carte est divisé par deux. Je vais.
La couche * ** conv2d_2 ** est également une couche convolutive avec une taille de noyau de $ 1x2 $ et une foulée de $ 1x2
. Le nombre de noyaux est spécifié comme 8. Le pliage ici est pour les informations de planche "ASK côté prix / quantité plié avec conv2d_1" et "BID côté prix / quantité plié avec conv2d_1", si le meilleur signe À propos du meilleur devis Il joue le rôle de rassembler les quatre nombres de prix et de quantité ASK et BID. En fonction des poids de conv2d_1 et conv2d_2, vous pouvez obtenir une petite image lorsque vous pensez au comportement de calcul du point médian moyen pondéré des ASK et BID correspondants. Ce point médian moyen pondéré est également appelé microprix ( p_t ^ {(micro)} $) et est défini comme suit.
$ \ quad p_ {t, i} ^ {(micro)} = \ frac {P_ \ {t, i} ^ {demander} V_ \ {t, i} ^ {demander} + P_ \ {t, i} ^ {bid} V_ \ {t, i} ^ {bid}} {V_ \ {t, i} ^ {ask} + V_ \ {t, i} ^ {bid}} $ - ** La couche conv2d_3 ** est une couche convolutive avec une taille de noyau de 1 $ x 10 $ et une foulée de 1 $. Le nombre de noyaux est spécifié comme 8. En premier lieu, les deux côtés de ASK et BID font référence à 10 cartes, donc la sortie de conv2d_2 se compose de 10 nombres pour chaque information de carte. C'est cette couche qui plie ces 10 nombres ensemble. Les informations du tableau à ce stade ont été regroupées en un seul chiffre. Le calque * ** reshape_1 ** est là pour transmettre la sortie de conv2d_3 au lstm_1 suivant. La couche * ** ltsm_1 ** tente de capturer les relations chronologiques des informations de la carte qui ont été réduites jusqu'à présent. Le nombre d'unités spécifie 8. La couche * ** dense_1 ** est une simple couche cachée qui reçoit la sortie de LSTM. La couche * ** dense_2 ** est la couche de sortie de ce réseau. Trois sorties sont utilisées en fonction du nombre de types d'étiquettes et softmax est utilisé pour l'activation.
5. Mise en œuvre
Prétraitement des données
- Ici, nous déplacerons le modèle en utilisant les données de la 5ème marque avec le plus grand nombre d'échantillons parmi les données lues précédemment.
#Les informations sur le conseil se trouvent dans les 40 premières lignes. 29738 comme données de la cinquième marque~Spécifiez 47294.
lob = data.iloc[:40, 29738:47294].T.values
#Ici, standardisez par prix et quantité.
lob = lob.reshape(-1,2)
lob = (lob - lob.mean(axis=0)) / lob.std(axis=0)
lob = lob.reshape(-1,40)
lob_df = pd.DataFrame(lob)
#Calculez le point médian non standardisé.
lob_df['mid'] = (data.iloc[0,29738:47294].T.values + data.iloc[2,29738:47294].T.values) / 2
- Lorsque je trace le prix médian, cela ressemble à ce qui suit. Eh bien, c'est un graphique boursier commun. On a l'impression qu'il y a beaucoup de petites vibrations car il n'y a pas de prix limite pour tous les prix de soumission qui sont proches du prix actuel. Le fait que le cours de l'action ne soit pas une donnée qui continue d'évoluer dans une direction semble être une bonne chose pour créer un modèle.
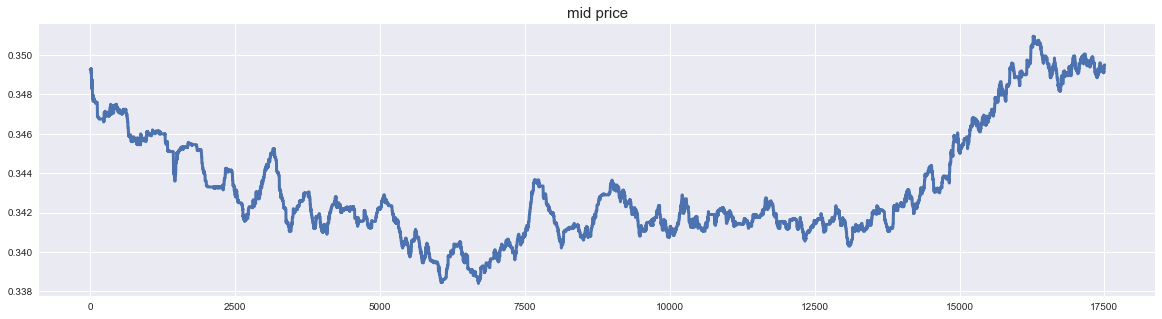
- Ensuite, nous allons créer une étiquette.
#Spécifiez les paramètres.
p = 50
k = 50
alpha = 0.0003
#Créez une étiquette à partir du milieu en fonction des paramètres.
lob_df['lt'] = (lob_df['mid'].rolling(window=k).mean().shift(-k)-lob_df['mid'])/lob_df['mid']
lob_df = lob_df.dropna()
lob_df['label'] = 0
lob_df.loc[lob_df['lt']>alpha, 'label'] = 1
lob_df.loc[lob_df['lt']<-alpha, 'label'] = -1
-
L'étiquetage avec ce paramètre ressemble à ce qui suit. Lorsque le cours de l'action augmente, il envoie un signal à la hausse et lorsqu'il baisse, il envoie un signal à la baisse.
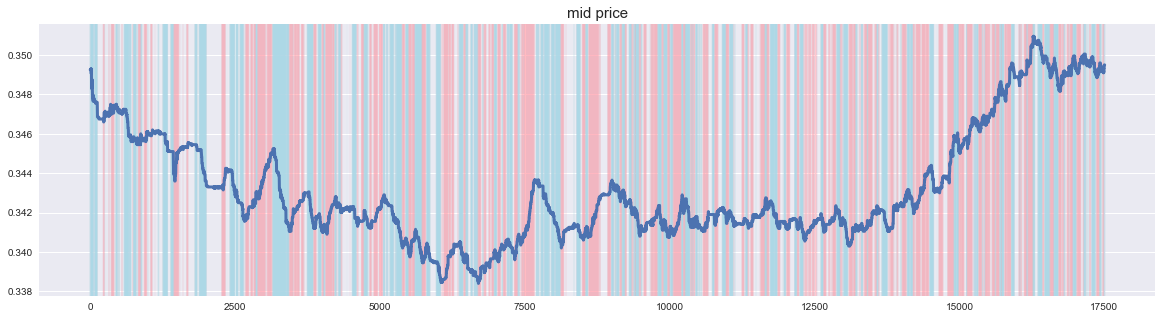
-
Chargez la bibliothèque requise.
from sklearn.model_selection import train_test_split
from keras.utils import to_categorical
from keras.layers import Conv2D, Dense, Reshape, Input, LSTM
from keras import Model, backend
import tensorflow as tf
- Nous créerons des données d'entraînement.
#Créez des données d'entraînement.
X = np.zeros((len(lob_df)-p+1, p, 40, 1))
lob = lob_df.iloc[:,:40].values
for i in range(len(lob_df)-p+1):
X[i] = lob[i:i+p,:].reshape(p,-1,1)
y = to_categorical(lob_df['label'].iloc[p-1:], 3)
print(X.shape, y.shape)
#=> (17457, 50, 40, 1) (17457, 3)
- Enfin, divisez en données d'entraînement et données de test.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
- Ceci termine le prétraitement!
Construction de modèles
- À partir de là, nous allons créer un modèle du réseau neuronal à l'aide de keras. Je suis plus familier avec l'API fonctionnelle que Sequential, je vais donc l'écrire ici.
tf.reset_default_graph()
backend.clear_session()
inputs = Input(shape=(p,40,1))
x = Conv2D(8, kernel_size=(1,2), strides=(1,2), activation='relu')(inputs)
x = Conv2D(8, kernel_size=(1,2), strides=(1,2), activation='relu')(x)
x = Conv2D(8, kernel_size=(1,10), strides=1, activation='relu')(x)
x = Reshape((p, 8))(x)
x = LSTM(8, activation='relu')(x)
x = Dense(16, activation='relu')(x)
outputs = Dense(3, activation='softmax')(x)
model = Model(inputs=inputs, outputs=outputs)
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
Apprenons!
- Tout ce que vous avez à faire est d'apprendre.
epochs = 50
batch_size = 256
history = model.fit(X_train, y_train,
epochs=epochs,
batch_size=batch_size,
verbose=1,
validation_data=(X_test, y_test))
Epoch 100/100 13965/13965 [==============================] - 5s 326us/step - loss: 0.6526 - acc: 0.6808 - val_loss: 0.6984 - val_acc: 0.6595
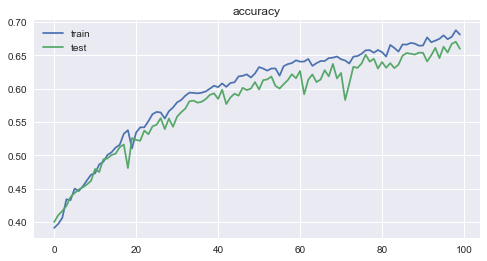
- La perte et la précision pour chaque époque sont les suivantes. Vous pouvez voir comment l'apprentissage progresse raisonnablement bien.

6. Examen
-
La précision était de 0,6808 pour les données d'entraînement et de 0,6595 ** pour les données de test, ce qui était un résultat étonnamment bon.
-
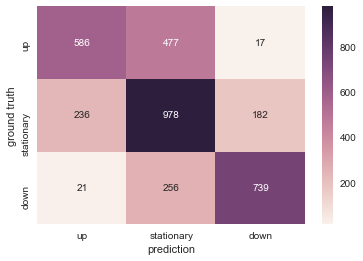
Visualisons le résultat des données de test avec une carte thermique. Il est bon qu'ils puissent être classés correctement, mais compte tenu de l'application pratique, «donner un signal à la baisse lorsque le cours de l'action augmente» et «donner un signal à la hausse lorsque le cours de l'action baisse» conduisent à une perte. C'est donc le plus problématique. À cet égard, il existe de nombreux cas où le signal opposé est donné, ce qui est un résultat positif.
-
Tâches futures
-
Hyper réglage des paramètres.
-
Apprenez également les données d'autres marques.
-
Apprenez à utiliser les données d'autres jours de négociation. (En général, on sait que même si un modèle est créé sur la base des données d'un jour, les performances se détérioreront s'il est utilisé un autre jour.)
-
Vérifier si des performances similaires peuvent être obtenues sur le récent marché boursier japonais.
Recommended Posts