Reproduction sur plaque de régression linéaire bayésienne (PRML §3.3)

salutation

Je suis @naoya_t, le secrétaire du Machine Learning Advent Calendar 2013, qui a commencé aujourd'hui. J'ai hâte de travailler à nouveau avec vous cette année. (Le jour a changé à l'heure du Japon. Je suis désolé qu'il soit très tard. J'étais juste à temps pour l'heure standard argentine (GMT-3)!)

Le contenu de cet article du calendrier de l'Avent convient à tout ce qui concerne la science des données, comme la reconnaissance de formes, l'apprentissage automatique, le traitement du langage naturel et l'exploration de données. Le montant n'a pas d'importance tant qu'il suit le thème. (Résumé des parties lues telles que PRML, MLaPP, etc., essayées de mettre en œuvre, introduction sur papier, développement de formules, etc.)

Profitons ensemble avec tous ceux qui écrivent et tous ceux qui ne font que lire!

Sujet du jour

Aujourd'hui, puisqu'il s'agit d'un sujet léger de PRML que tout le monde aime, je voudrais reproduire les figures 3.8 et 3.9 de "Bayes Linear Regression" au §3.3.

図3.8 図3.9

Je pensais dessiner un graphe 3D du noyau équivalent (Fig. 3.10), mais le temps était écoulé. (Je l'ajouterai quand j'en aurai envie!)

Calcul requis

La légende de la figure 3.8 dit: «Le modèle se compose de neuf fonctions gaussiennes (de base) de la forme (3.4)». Fonction de base gaussienne $ \ phi_j (x) = exp \ left (- \ frac {(x- \ mu_j) ^ 2} {2s ^ 2} \ right) $ dans la plage de x = [0,1] Je vais essayer d'en organiser 9 uniformément.

figure 3.8 est la distribution préditep(t|\mathbf{x},\mathbf{t},\alpha,\beta)=N(t|\mathbf{m}_N\mathbf{\phi(x)},\sigma_N^2(\mathbf{x})) (3.58)Vous pouvez dessiner si vous pouvez obtenir la moyenne et la variance de. Nécessaire pour cela $ \ mathbf {m} _N $, $ \ mathbf {S} _N $, $ \ sigma_N ^ 2 (\ mathbf {x}) $

\mathbf{S}_N^{-1}=\alpha I+\beta\Phi^\mathrm{T}\Phi (3.54)
\mathbf{m}_N=\beta\mathbf{S}_N\Phi^\mathrm{T}\mathbf{t} (3.53)
\sigma_N^2(\mathbf{x})=\frac1\beta+\mathbf{\phi(x)}^\mathrm{T}\mathbf{S}_N\mathbf{\phi(x)} (3.59)

Il peut être trouvé par. Le $ \ Phi $ qui apparaît ici est la matrice de planification (3.16) que tout le monde connaît. Assemblez à partir de la fonction de base $ \ phi_j (x) $ et des données d'entrée $ \ mathbf {x} $.

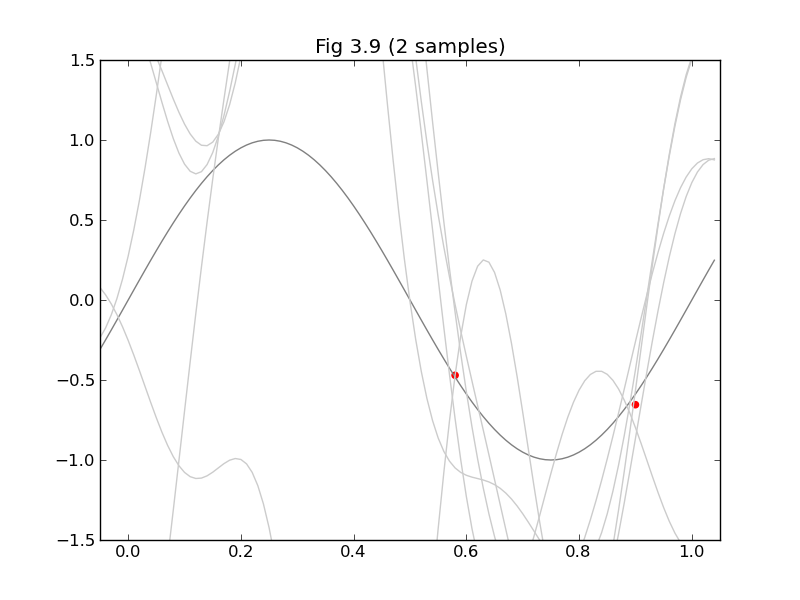
figure 3.9 est\mathbf{w}Distribution postérieure dep(\mathbf{w}|\mathbf{t})=N(\mathbf{w}|\mathbf{m}_N,\mathbf{S}_N) (3.49)De\mathbf{w}Échantillonnage de 5 chacun, environ chacuny(x,\mathbf{w})=\mathbf{w}^\mathrm{T}\mathbf{\phi(x)}Juste complot.

code

`fig38_39.py`


#!/usr/bin/env python
# -*- coding: utf-8 -*-

from pylab import *

S     = 0.1
ALPHA = 0.1
BETA  = 9

def sub(xs, ts):
    # φj(x)Adopte la fonction de base gaussienne
    def gaussian_basis_func(s, mu):
        return lambda x:exp(-(x - mu)**2 / (2 * s**2))

    # φ(x)
    def gaussian_basis_funcs(s, xs):
        return [gaussian_basis_func(s, mu) for mu in xs]

    xs9 = arange(0, 1.01, 0.125) # 9 points
    bases = gaussian_basis_funcs(S, xs9)

    N = size(xs) #Score des données
    M = size(bases) #Nombre de fonctions de base

    def Phi(x):
        return array([basis(x) for basis in bases])

    # Design matrix
    PHI = array(map(Phi, xs))
    PHI.resize(N, M)

    # predictive distribution
    def predictive_dist_func(alpha, beta):
        S_N_inv = alpha * eye(M) + beta * dot(PHI.T, PHI)
        m_N = beta * solve(S_N_inv, dot(PHI.T, ts)) # 20.1

        def func(x):
            Phi_x = Phi(x)
            mu = dot(m_N.T, Phi_x)
            s2_N = 1.0/beta + dot(Phi_x.T, solve(S_N_inv, Phi_x))
            return (mu, s2_N)

        return m_N, S_N_inv, func

    xmin = -0.05
    xmax =  1.05
    ymin = -1.5
    ymax =  1.5

    #
    #figure 3.8
    #
    clf()
    axis([xmin, xmax, ymin, ymax])
    title("Fig 3.8 (%d sample%s)" % (N, 's' if N > 1 else ''))

    x_ = arange(xmin, xmax, 0.01)
    plot(x_, sin(x_*pi*2), color='gray')

    m_N, S_N_inv, f = predictive_dist_func(ALPHA, BETA)

    y_h = []
    y_m = []
    y_l = []
    for mu, s2 in map(f, x_):
        s = sqrt(s2)
        y_m.append(mu)
        y_h.append(mu + s)
        y_l.append(mu - s)

    fill_between(x_, y_h, y_l, color='#cccccc')
    plot(x_, y_m, color='#000000')

    scatter(xs, ts, color='r', marker='o')
    show()

    #
    #figure 3.9
    #
    clf()
    axis([xmin, xmax, ymin, ymax])
    title("Fig 3.9 (%d sample%s)" % (N, 's' if N > 1 else ''))

    x_ = arange(xmin, xmax, 0.01)
    plot(x_, sin(x_*pi*2), color='gray')

    for i in range(5):
        w = multivariate_normal(m_N, inv(S_N_inv), 1).T
        y = lambda x: dot(w.T, Phi(x))[0]
        plot(x_, y(x_), color='#cccccc')

    scatter(xs, ts, color='r', marker='o')
    show()


def main():
    #Exemple de données (ajoute du bruit gaussien)
    xs = arange(0, 1.01, 0.02)
    ts = sin(xs*pi*2) + normal(loc=0.0, scale=0.1, size=size(xs))

    #Choisissez un nombre approprié à partir des exemples de données
    def randidx(n, k):
        r = range(n)
        shuffle(r)
        return sort(r[0:k])

    for k in (1, 2, 5, 20):
        indices = randidx(size(xs), k)
        sub(xs[indices], ts[indices])


if __name__ == '__main__':
    main()

l'a fait!

À la fin

L'année dernière, il a été souligné que j'avais trop sauté dès le premier jour, donc ce n'est pas à cause du moment de la rédaction, mais cette année, je suis désolé de ne pas pouvoir répondre aux attentes de tout le monde avec un thème un peu plus léger.

Le responsable de 12/2 est @ puriketu99. Restez à l'écoute!