Régression linéaire avec statsmodels

J'avais l'habitude d'utiliser scipy.stats.linregress comme régression linéaire de Python, mais j'ai introduit statsmodels car il a peu de fonctions et est difficile à utiliser. Je ne l'ai utilisé que pendant 2 heures, donc j'ai peut-être mal compris quelque chose de fondamentalement. Je ne l'ai utilisé que pendant 2 heures, donc je suis désolé

Ce qui suit décrit comment utiliser OLS (méthode des moindres carrés ordinaires; méthode des moindres carrés ordinaires) des statsmodels. Cliquez ici pour les documents officiels http://statsmodels.sourceforge.net/stable/regression.html

Installation

Habituellement avec pip.

$ sudo pip install statsmodels

Le code ci-dessous utilise également numpy et matplotlib, alors installez-les si vous ne les avez pas.

$ sudo pip install numpy
$ sudo pip install matplotlib

Exemple simple

Pour le moment, comme exemple le plus simple

y = a + bx + \varepsilon

Considérez la régression linéaire dans le modèle. En d'autres termes, étant donné les données de $ (x_i, y_i) $, le paramètre $ (a, b) $ est déterminé de sorte que l'erreur $ \ sum \ varepsilon_i ^ 2 $ soit minimisée.

Par exemple, supposons que vous ayez les données suivantes. Ce sont les données que j'ai faites maintenant, et si je répondais d'abord, ce serait a = 1.0, b = 3.0, mais je fais semblant de ne pas le savoir et je le trouve par régression.

data.txt

#      x        y
  -1.000   -1.656
  -0.900   -0.734
  -0.800   -3.036
  -0.700   -1.026
  -0.600   -1.104
  -0.500    0.023
  -0.400    0.246
  -0.300    1.817
  -0.200    0.651
  -0.100    0.082
  -0.000    2.524
   0.100    2.231
   0.200    0.783
   0.300    2.489
   0.400    1.892
   0.500    3.207
   0.600    1.868
   0.700    3.954
   0.800    4.447
   0.900    4.024

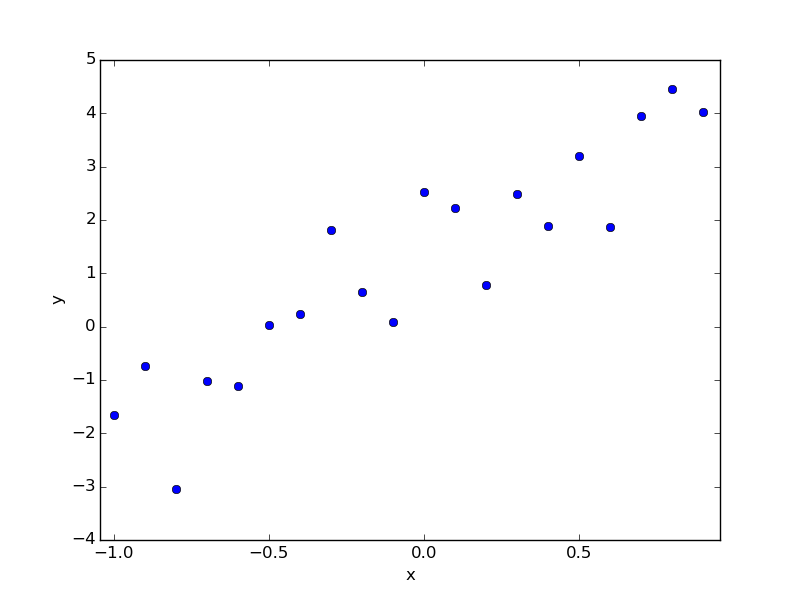
Le retour à ceci est le suivant.

regression.py

# coding: utf-8
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt

#Lire les données
data = np.loadtxt("data.txt")
x = data.T[0]
y = data.T[1]

#Nombre d'échantillons
nsample = x.size

#la magie(Commentaire plus tard)
X = np.column_stack((np.repeat(1, nsample), x))

#Exécution de la régression
model = sm.OLS(y, X)
results = model.fit()

#Afficher le résumé des résultats
print results.summary()

#Obtenir des estimations de paramètres
a, b = results.params

#Afficher le tracé
plt.plot(x, y, 'o')
plt.plot(x, a+b*x)
plt.text(0, 0, "a={:8.3f}, b={:8.3f}".format(a,b))
plt.show()

Une fois exécuté, le texte et le graphique suivants seront affichés.

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.831
Model:                            OLS   Adj. R-squared:                  0.822
Method:                 Least Squares   F-statistic:                     88.59
Date:                Thu, 25 Dec 2014   Prob (F-statistic):           2.25e-08
Time:                        14:07:16   Log-Likelihood:                -24.450
No. Observations:                  20   AIC:                             52.90
Df Residuals:                      18   BIC:                             54.89
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [95.0% Conf. Int.]
------------------------------------------------------------------------------
const          1.2922      0.194      6.647      0.000         0.884     1.701
x1             3.1611      0.336      9.412      0.000         2.455     3.867
==============================================================================
Omnibus:                        0.801   Durbin-Watson:                   2.495
Prob(Omnibus):                  0.670   Jarque-Bera (JB):                0.653
Skew:                          -0.402   Prob(JB):                        0.721
Kurtosis:                       2.628   Cond. No.                         1.74
==============================================================================

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Ce sera comme ça.

Modèle de fonction de base linéaire

Dans le modèle mentionné ci-dessus, la relation entre x et y était une expression linéaire, mais dans la vie, nous voulons souvent envisager une relation plus compliquée entre x et y. Par conséquent, en utilisant un modèle de fonction de base linéaire, il devient possible d'exprimer une relation relativement diverse entre x et y.

y = \beta_0 + \beta_1 \phi_1(x) + \beta_2\phi_2(x) + \cdots + \beta_{M-1}\phi_{M-1}(x) + \varepsilon

Ici, $ x et y $ sont des données, $ \ phi_j (x) $ est une fonction connue, et $ \ beta_j $ est un paramètre à obtenir. Notez que cette formule peut être facilement définie sur $ \ phi_0 (x) \ equiv 1 $.

y = \sum_{j=0}^{M-1} \beta_j\phi_j(x) + \varepsilon

Peut également être écrit. Par exemple, si $ M = 3, \ phi_1 (x) = x, \ phi_2 (x) = x ^ 2 $, alors la fonction quadratique $ y = \ beta_0 + \ beta_1x + \ beta_2x ^ 2 + \ varepsilon $ ..

Lorsque vous effectuez une régression avec statsmodels, il vous suffit de saisir les informations pour les données $ (x_i, y_i) $ et la fonction connue $ \ phi_j (x) $, mais il est difficile de saisir directement les informations de la fonction, donc $ Entrez la matrice suivante qui résume les informations de x_i $ et $ \ phi_j (x_i) $. (Lorsque M = 3)

X = \begin{Bmatrix}
\phi_0(x_0) & \phi_1(x_0) & \phi_2(x_0) \\
\phi_0(x_1) & \phi_1(x_1) & \phi_2(x_1) \\
\phi_0(x_2) & \phi_1(x_2) & \phi_2(x_2) \\
& \vdots & \\
\end{Bmatrix}

Ici, $ \ phi_0 (x) \ equiv 1 $, donc la première colonne de cette matrice est toute 1. C'est pourquoi j'ai ajouté la colonne np.repeat (1, nsample) `dans le code précédent comme" magic ".

Donc, si nous changeons la façon dont cette matrice X est créée, la régression linéaire de n'importe quel modèle sera possible.

Exemple un peu compliqué

Par exemple

y = a + bx + cx^2 + \varepsilon

Considérez le modèle. Tout ce que vous avez à faire est d'ajouter une colonne correspondant à $ x ^ 2 $ à la partie de la matrice X dans le code précédent. Tout d'abord, préparez l'ensemble de données. Comme d'habitude, la réponse est a = 3.0, b = 1.0, c = 2.0.

data.txt

#      x        y
  -2.000   10.260
  -1.800    7.403
  -1.600    7.779
  -1.400    4.310
  -1.200    4.051
  -1.000    4.577
  -0.800    3.416
  -0.600    3.628
  -0.400    3.968
  -0.200    3.780
  -0.000    1.873
   0.200    2.741
   0.400    2.106
   0.600    5.286
   0.800    8.138
   1.000    5.316
   1.200    9.159
   1.400    9.748
   1.600    7.585
   1.800   10.726

Le code est ci-dessous. Cependant, je n'ai changé que la partie où la matrice X a été créée et le numéro des derniers paramètres.

regression_2.py

# coding: utf-8
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt

#Lecture des données
data = np.loadtxt("data.txt")
x = data.T[0]
y = data.T[1]

#Nombre d'échantillons
nsample = x.size

#Création de la matrice X
X = np.column_stack((np.repeat(1, nsample), x, x**2))

#Effectuer une régression
model = sm.OLS(y, X)
results = model.fit()

#Afficher le résumé des résultats
print results.summary()

#Obtenir des estimations de paramètres
a, b, c = results.params

#Afficher sous forme de graphique
plt.plot(x, y, 'o')
plt.plot(x, a+b*x+c*x**2)
plt.title("a={:.4f}, b={:.4f}, c={:.4f}".format(a,b,c))
plt.show()

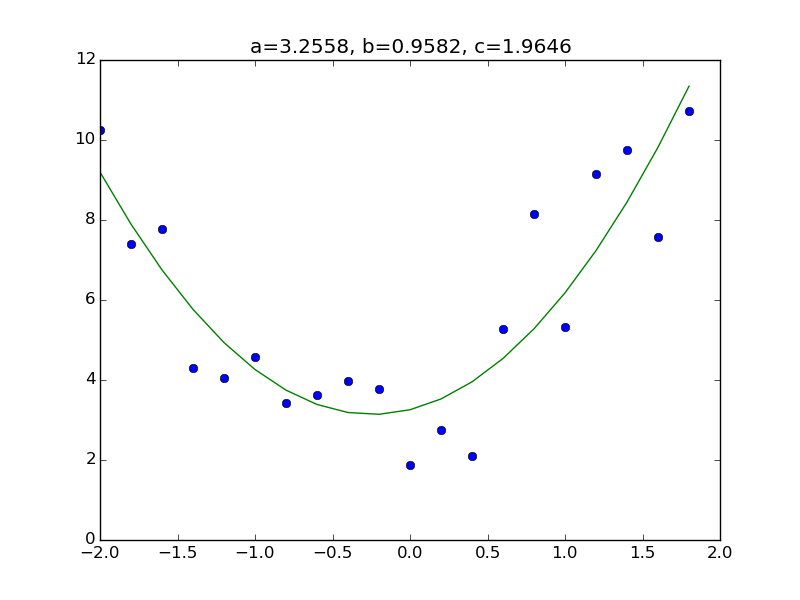
Autre

En plus de OLS (méthode du carré minimum ordinaire), statsmodels a également WLS (méthode du carré minimum pondéré), alors écrivez-le si vous en avez envie.