Cet article est le 12ème jour du Calendrier de l'Avent JavaFX 2016. Hier, c'est [Scene Builder 3 petites histoires] de @ skrb (http://skrb.hatenablog.com/entry/2016/12/11/000300). Demain, c'est @ sk44_.

introduction

JavaFX Canvas a une fonction graphique 2D qui dessine des données vectorielles et des données d'image telles que des lignes, des rectangles, des ellipses et des polygones. Vous pouvez également spécifier des transformations affines pour transformer des dessins 2D tels que l'agrandissement, la réduction, le mouvement parallèle, la rotation et le cisaillement.

Supposons maintenant que vous puissiez utiliser la conversion Affin pour afficher des données 2D plus grandes que l'écran en les agrandissant ou en les réduisant arbitrairement, ou en les faisant défiler vers le haut, le bas, la gauche ou la droite pour les afficher. Les exemples incluent l'affichage de la carte et l'affichage des données CAO.

Le principe de la transformation affine semble simple, mais il rentre souvent dans le jeu quand je l'essaie, et il y a deux ans [la transformation affine dans Canvas convient beaucoup (je n'avais pas assez de sens mathématique ...)]( J'ai même écrit un blog appelé http://d.hatena.ne.jp/torutk/20140415/p1).

Lors du JJUG CCC 2016 Automne qui s'est tenu le 3 de ce mois, nous avons annoncé le contenu du dessin de données cartographiques (données du littoral mondial) avec JavaFX Canvas sous le titre "Le monde n'est pas un carré-tracer une carte avec JavaFX". Dans le programme d'exemple d'affichage de carte préparé à ce moment, l'agrandissement / la réduction / le défilement est effectué à l'aide de la conversion Affin. Cependant, il y avait un problème en ce que la position de la carte affichée se déplaçait lors de l'agrandissement / réduction. Malheureusement, il n'a pas pu être résolu le jour de l'annonce.

Par conséquent, pour me venger, lors de l'agrandissement / réduction de l'affichage, j'ai décidé de réétudier la conversion Affin à partir des bases et de l'organiser de manière à ce que le centre des données affichées à l'écran ne se déplace pas.

Environnement d'exécution de cet article

Cet article est écrit dans le but d'étudier et de comprendre la conversion affine JavaFX, il n'y a donc pas d'exemple de programme. Pour vérifier facilement le fonctionnement de la conversion Affine, j'utilise l'environnement de ligne de commande jshell qui sera inclus dans JDK 9, qui sortira l'année prochaine.

Sur l'environnement Windows 10 64 bits, j'ai mis Java SE Development Kit 9 Early Access version et j'utilise la commande shell. Au moment de la rédaction de cet article, il s'agit de la version JDK 9 Build 148.

Système de coordonnées de données et système de coordonnées d'écran

Généralement, la forme des données est définie dans le système de coordonnées orthogonales. Ce système de coordonnées orthogonales représente le système droitier, c'est-à-dire la direction dans laquelle la direction positive de l'axe x est tournée de 90 degrés dans le sens antihoraire en tant que direction positive de l'axe y.

D'autre part, les coordonnées de l'écran JavaFX sont également définies dans le système de coordonnées orthogonales, qui représente le système de gauche, c'est-à-dire la direction dans laquelle la direction positive de l'axe x est tournée de 90 degrés dans le sens des aiguilles d'une montre comme la direction positive de l'axe y. ..

データ座標系と画面座標系.png

Par conséquent, si les coordonnées des données sont affichées à l'écran telles quelles, elles seront à l'envers.

Lors de l'affichage des données cartographiques sans conversion ...

Les données cartographiques sont généralement définies en coordonnées de latitude et de longitude. L'exprimer sur l'axe des y pour la latitude et sur l'axe des x pour la longitude donne les données suivantes.

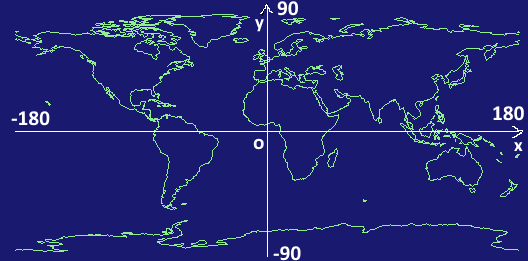
Si ces données cartographiques sont affichées à l'écran sans aucune conversion de coordonnées, l'affichage sera comme suit.

La plage du premier quadrant (0,0) à (180,90) du système de coordonnées des données cartographiques est affichée à l'envers.

Par conséquent, nous allons introduire une conversion de coordonnées du système de coordonnées de données vers le système de coordonnées d'écran afin que les données puissent être affichées en agrandissant / réduisant arbitrairement / déplacement parallèle / rotation. La transformation de coordonnées utilisée à ce moment est la transformation affine.

Conversion du système de coordonnées de données en système de coordonnées d'écran par conversion Affin

Soit le système de coordonnées des données le système de coordonnées xy et le système de coordonnées d'écran le système de coordonnées x'y '. En supposant que les points sur le système de coordonnées xy sont (x, y) et les points sur le système de coordonnées x'y 'sont (x', y '), la conversion des coordonnées du système de coordonnées des données vers le système de coordonnées de l'écran est (x, y). ) Est l'entrée et (x ', y') est la sortie.

x' = ax + by + t_x\\
y' = cx + dy + t_y

Lorsque cette formule de conversion est réexprimée sous forme de vecteur de coordonnées et de matrice de conversion,

\begin{pmatrix}
x'\\ 
y'\\
1
\end{pmatrix}
= \begin{pmatrix}
a & b & t_x\\
c & d & t_y\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
1
\end{pmatrix}

Ce sera. Cette matrice devient la matrice de transformation affine. (Dans le cas de 2 dimensions) En termes de traitement du calcul, il est calculé avec un vecteur / matrice cubique (coordonnées du même ordre).

Transformation de coordonnées (1): transformation uniforme

x' = x\\
y' = y\\

Si vous appliquez la conversion (c'est-à-dire ne convertissez rien), l'affichage sera à l'envers. Exprimé par conversion Affin, il se présente comme suit.

\begin{pmatrix}
x'\\y\\1'
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\y\\1
\end{pmatrix}

Avec cette conversion (pas de conversion), les données s'affichent à l'écran comme suit.

データ座標→画面座標（恒等変換）.png

La partie rectangulaire jaune est la zone de dessin d'écran. Les points A, B et C sont convertis (sans conversion) en A ', B', C 'comme suit.

\begin{align*}
(A'_x, A'_y) &= (A_x, A_y) = (160, 200)\\
(B'_x, B'_y) &= (B_x, B_y) = (320, 0)\\
(C'_x, C'_y) &= (C_x, C_y) = (160, -200)
\end{align*}

Cette transformation affine est créée avec le code suivant.

Affine affine = new Affine();

Expérimentation d'Affine dans l'environnement jshell du JDK 9

Placez la variable d'environnement PATH dans JDK 9. Exécutez jshell.

C:\>java -version
java version "9-ea"
Java(TM) SE Runtime Environment (build 9-ea+148)
Java HotSpot(TM) 64-Bit Server VM (build 9-ea+148, mixed mode)

C:\>jshell
|Bienvenue dans JShell--Version 9-ea
|Pour un aperçu, tapez: /help intro
|
jshell>

Génère une transformation affine (transformation égale).

jshell> import javafx.scene.transform.Affine

jshell> Affine affine = new Affine()
affine ==> Affine [
        1.0, 0.0, 0.0, 0.0
        0.0, 1.0, 0.0, 0.0
        0.0, 0.0, 1.0, 0.0
]

L'environnement jshell est pratique car il affiche le contenu des variables définies. Cependant, il est affiché sur 3 lignes et 4 colonnes. En effet, JavaFX est fourni en standard avec des graphiques 3D afin de pouvoir gérer les transformations de coordonnées 3D.

Lorsque vous traitez des transformations affines 2D, ne vous inquiétez pas pour la troisième colonne, comme indiqué ci-dessus.

Ensuite, créons un point dans le système de coordonnées des données et convertissons-le avec cette affine.

jshell> import javafx.geometry.Point2D

jshell> Point2D dataA = new Point2D(160, 200)
dataA ==> Point2D [x = 160.0, y = 200.0]

jshell> affine.transform(dataA)
$5 ==> Point2D [x = 160.0, y = 200.0]

jshell>

Des coordonnées avec les mêmes valeurs que les coordonnées d'origine (160 200) ont été obtenues à la suite de cette conversion affine.

Conversion de coordonnées (2): élimination de la tête en bas

Puisque l'axe y est inversé, nous pensons que nous pouvons simplement inverser le signe de la coordonnée y et introduire la transformation de coordonnées suivante.

\begin{align*}
x' &= x\\
y' &= -y\\
\end{align*}

Exprimé par conversion Affin, il se présente comme suit.

\begin{pmatrix}
x'\\y'\\1
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & 0\\
0 & -1 & 0\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\y\\1
\end{pmatrix}

データ座標→画面座標（上下反転）.png

Les points A, B et C sont convertis en A ', B', C 'comme suit.

\begin{align*}
(A'_x, A'_y) &= (A_x, -A_y) = (160, -200)\\
(B'_x, B'_y) &= (B_x, -B_y) = (320, 0)\\
(C'_x, C'_y) &= (C_x, -C_y) = (160, 200)
\end{align*}

L'affichage des données a été résolu à l'envers, mais la zone d'affichage des données n'est pas alignée avec la zone d'affichage de (Partie 1) (en face de l'axe X).

Cette transformation affine est créée avec le code suivant.

Affine affine = new Affine(1, 0, 0, 0, -1, 0);

Expérimentation d'Affine dans l'environnement jshell du JDK 9

jshell> affine = new Affine(1, 0, 0, 0, -1, 0)
affine ==> Affine [
        1.0, 0.0, 0.0, 0.0
        0.0, -1.0, 0.0, 0.0
        0.0, 0.0, 1.0, 0.0
]

jshell> affine.transform(dataA)
$9 ==> Point2D [x = 160.0, y = -200.0]

jshell>

Le point A a été converti de (160, 200) à (160, -200). De même, voyons les résultats de conversion pour les points B et C.

jshell> Point2D dataB = new Point2D(320, 0)
dataB ==> Point2D [x = 320.0, y = 0.0]

jshell> affine.transform(dataB)
$12 ==> Point2D [x = 320.0, y = -0.0]

jshell> Point2D dataC = new Point2D(160, -200)
dataC ==> Point2D [x = 160.0, y = -200.0]

jshell> affine.transform(dataC)
$13 ==> Point2D [x = 160.0, y = 200.0]

jshell>

Le point B a été converti de (320, 0) à (320, -0) (les valeurs de coordonnées ne changent pas). Le point C a été converti de (160, -200) à (160, 200).

Conversion de coordonnées (3): mouvement parallèle d'origine

L'origine du système de coordonnées de données est le coin inférieur gauche de la zone que vous souhaitez dessiner, mais l'origine du système de coordonnées d'écran est le coin supérieur gauche de la zone à dessiner. Par conséquent, déplacez l'origine du système de coordonnées de données parallèlement à l'origine du système de coordonnées d'écran pour correspondre à la zone que vous souhaitez dessiner.

Dans ce cas, le mouvement parallèle correspond à la hauteur de la zone de dessin dans la direction de l'axe y. Si la hauteur de la zone de dessin est h, la formule de conversion est la suivante.

\begin{align*}
x' &= x\\
y' &= -(y - h) = -y + h\\
\end{align*}

Exprimé par conversion Affin, il se présente comme suit.

\begin{pmatrix}
x'\\y'\\1
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & 0\\
0 & -1 & h\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\y\\1
\end{pmatrix}

Le chiffre et chaque coordonnée lorsque la hauteur h est de 200 sont les suivants.

データ座標→画面座標（上下反転＋原点一致）.png

\begin{align*}
(A'_x, A'_y) &= (A_x, -A_y + 200) = (160, 0)\\
(B'_x, B'_y) &= (B_x, -B_y + 200) = (320, 200)\\
(C'_x, C'_y) &= (C_x, -C_y + 200) = (160, 0)
\end{align*}

Cette transformation affine est créée avec le code suivant.

Affine affine = new Affine(1, 0, 0, 0, -1, 200);

Expérimentation d'Affine dans l'environnement jshell du JDK 9

jshell> affine = new Affine(1, 0, 0, 0, -1, 200)
affine ==> Affine [
        1.0, 0.0, 0.0, 0.0
        0.0, -1.0, 0.0, 200.0
        0.0, 0.0, 1.0, 0.0
]

jshell> affine.transform(dataA)
$19 ==> Point2D [x = 160.0, y = 0.0]

jshell> affine.transform(dataB)
$20 ==> Point2D [x = 320.0, y = 200.0]

jshell> affine.transform(dataC)
$21 ==> Point2D [x = 160.0, y = 400.0]

jshell>

Le point A a été converti de (160, 200) à (160, 0). Le point B a été converti de (320, 0) à (320, 200). Le point C a été converti de (160, -200) à (160, 400).

Conversion de coordonnées (4): déplacer la zone de dessin

Déplacez la zone de dessin vers n'importe quelle partie du système de coordonnées des données. En supposant que les coordonnées du coin supérieur gauche de la zone de dessin sont (x1, y1), la formule suivante exprime un mouvement parallèle.

\begin{align*}
x' &= x - x_1\\
y' &= -(y - y_1) = -y + y_1
\end{align*}

Exprimé par conversion Affin, il se présente comme suit.

\begin{pmatrix}
x'\\y'\\1
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & -x_1\\
0 & -1 & y_1\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\y\\1
\end{pmatrix}

Le chiffre et chaque coordonnée lorsque (x1, y1) est (-280, 500) sont les suivants.

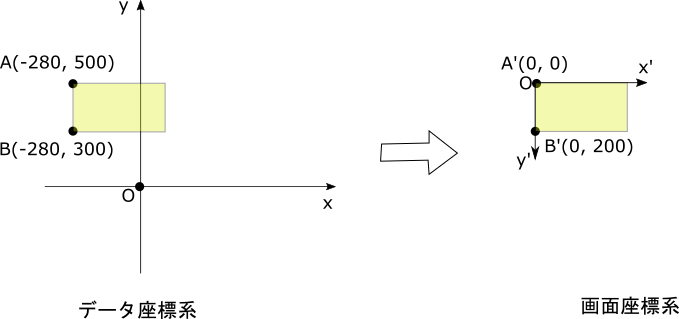
データ座標→画面座標（平行移動）.png

\begin{align*}
(A'_x, A'_y) &= (A_x - (-280), -(A_y - 500))\\
 &= (A_x + 280, -A_y + 500)\\
 &= (0, 0)\\
(B'_x, B'_y) &= (B_x - (-280), -(B_y - 500))\\
 &= (B_x + 280, -B_y + 500)\\
 &= (0, 200)
\end{align*}

Cette transformation affine est créée avec le code suivant.

Affine affine = new Affine(1, 0, 280, 0, -1, 500);

C'est un peu déroutant.

Considérez une combinaison de deux transformations de coordonnées.

Mouvement parallèle
À l'envers

La transformation affine de mouvement parallèle est exprimée par l'équation matricielle suivante.

\begin{pmatrix}
1 & 0 & -x_1\\
0 & 1 & -y_1\\
0 & 0 & 1
\end{pmatrix}

La transformation affine à l'envers est exprimée par l'équation matricielle suivante.

\begin{pmatrix}
1 & 0 & 0\\
0 & -1 & 0\\
0 & 0 & 1
\end{pmatrix}

Effectuez d'abord un mouvement parallèle, puis retournez-le. Dans ce cas, lors de la jonction de la matrice, écrivez celle à appliquer en premier sur le côté droit.

\begin{pmatrix}
1 & 0 & 0\\
0 & -1 & 0\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & -x_1\\
0 & 1 & -y_1\\
0 & 0 & 1
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & -x_1\\
0 & -1 & y_1\\
0 & 0 & 1
\end{pmatrix}

Expérimentation d'Affine dans l'environnement jshell du JDK 9

Combinez deux affines.

jshell> Affine affineMove = new Affine(1, 0, -(-280), 0, 1, -500)
affineMove ==> Affine [
        1.0, 0.0, 0.0, 280.0
        0.0, 1.0, 0.0, -500.0
        0.0, 0.0, 1.0, 0.0
]

jshell> Affine affineReverse = new Affine(1, 0, 0, 0, -1, 0)
affineReverse ==> Affine [
        1.0, 0.0, 0.0, 0.0
        0.0, -1.0, 0.0, 0.0
        0.0, 0.0, 1.0, 0.0
]

jshell> affineReverse.createConcatenation(affineMove)
$35 ==> Affine [
        1.0, 0.0, 0.0, 280.0
        0.0, -1.0, 0.0, 500.0
        0.0, 0.0, 1.0, 0.0
]

Eh bien, c'est encore difficile à comprendre ...

Maintenant, effectuons la conversion des coordonnées.

jshell> affine = new Affine(1, 0, 280, 0, -1, 500)
affine ==> Affine [
        1.0, 0.0, 0.0, 280.0
        0.0, -1.0, 0.0, 500.0
        0.0, 0.0, 1.0, 0.0
]

jshell> Point2D dataJ = new Point2D(-280, 500)
dataJ ==> Point2D [x = -280.0, y = 500.0]

jshell> affine.transform(dataJ)
$29 ==> Point2D [x = 0.0, y = 0.0]

jshell> Point2D dataK = new Point2D(-280, 300)
dataK ==> Point2D [x = -280.0, y = 300.0]

jshell> affine.transform(dataK)
$30 ==> Point2D [x = 0.0, y = 200.0]

Le système de coordonnées de données (-280, 500) a été converti en système de coordonnées d'écran (0, 0). Le système de coordonnées de données (-280, 300) a été converti en système de coordonnées d'écran (0, 200).

Conversion de coordonnées (5): mise à l'échelle et mouvement parallèle

Agrandit ou réduit la taille de la zone de dessin du système de coordonnées de données à n'importe quelle taille. En supposant que le rapport d'agrandissement est S et que les coordonnées du coin supérieur gauche de la zone de dessin sur le système de coordonnées de données sont (x1, y1), l'équation suivante exprime l'agrandissement / réduction et le mouvement parallèle.

\begin{align*}
x' &= s(x - x_1) = sx - sx_1\\
y' &= -s(y - y_1) = -sy + sy_1
\end{align*}

Exprimé par conversion Affin, il se présente comme suit.

\begin{pmatrix}
x'\\y'\\1
\end{pmatrix}=
\begin{pmatrix}
s & 0 & -sx_1\\
0 & -s & sy_1\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\y\\1
\end{pmatrix}

En cas de grossissement 2 et mouvement parallèle (0, 100)

Ici, regardons la zone d'affichage du système de coordonnées de données et la conversion en système de coordonnées d'écran lorsque le taux d'agrandissement est de 2 et la quantité de mouvement parallèle est (0,100).

データ座標→画面座標（スケール１）.png

Étant donné que le grossissement est doublé, la plage de 160x100 dans le système de coordonnées de données est dessinée dans le système de coordonnées d'écran 320x200.

\begin{align*}
(A'_x, A'_y) &= (2A_x +2.0, -2A_y +2.100)\\
 &= (0, 0)\\
(B'_x, B'_y) &= (2B_x +2.0, -2B_y +2.100)\\
 &= (320, 0)\\
(C'_x, C'_y) &= (2C_x +2.0, -2C_y +2.100)\\
 &= (320, 200)
\end{align*}

Le contenu des données ressemble à la figure suivante.

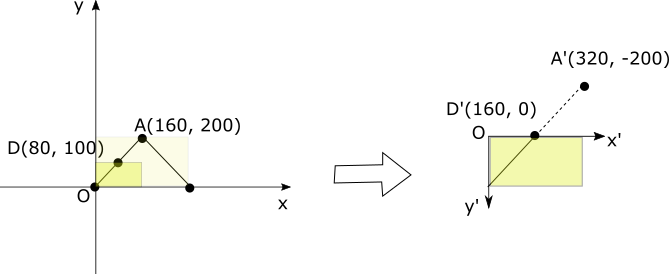
データ座標→画面座標（スケール）.png

Cette transformation affine est créée avec le code suivant.

Affine affine = new Affine(2, 0, 0, 0, -2, 200);

Expérimentation d'Affine dans l'environnement jshell du JDK 9

jshell> affine = new Affine(2, 0, 0, 0, -2, 200)
affine ==> Affine [
        2.0, 0.0, 0.0, 0.0
        0.0, -2.0, 0.0, 200.0
        0.0, 0.0, 1.0, 0.0
]

jshell> dataA = new Point2D(0, 100)
dataA ==> Point2D [x = 0.0, y = 100.0]

jshell> affine.transform(dataA)
$38 ==> Point2D [x = 0.0, y = 0.0]

jshell> dataB = new Point2D(160, 100)
dataB ==> Point2D [x = 160.0, y = 100.0]

jshell> affine.transform(dataB)
$40 ==> Point2D [x = 320.0, y = 0.0]

jshell> dataC = new Point2D(160, 0)
dataC ==> Point2D [x = 160.0, y = 0.0]

jshell> affine.transform(dataC)
$42 ==> Point2D [x = 320.0, y = 200.0]

Le système de coordonnées de données (0, 100) a été converti en système de coordonnées d'écran (0, 0). Le système de coordonnées de données (160, 100) a été converti en système de coordonnées d'écran (320, 0). Le système de coordonnées de données (160, 0) a été converti en système de coordonnées d'écran (320, 200).

Exemple avec un grossissement de 0,5 et un mouvement parallèle (100, 1000)

Le chiffre de conversion lorsque le grossissement est de 0,5 et la quantité de mouvement parallèle est (100,1000) est indiqué ci-dessous.

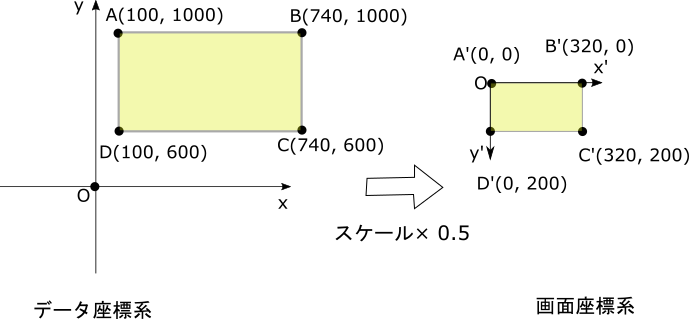
データ座標→画面座標（スケール＋平行移動）.png

La matrice de transformation affine à ce moment est la suivante.

\begin{pmatrix}
0.5 & 0 & -50\\
0 & -0.5 & 500\\
0 & 0 & 1
\end{pmatrix}

Expérimentation d'Affine dans l'environnement jshell du JDK 9

jshell> Affine affine = new Affine(0.5, 0, -50, 0, -0.5, 500)
affine ==> Affine [
        0.5, 0.0, 0.0, -50.0
        0.0, -0.5, 0.0, 500.0
        0.0, 0.0, 1.0, 0.0
]

jshell> affine.transform(100, 1000)
$4 ==> Point2D [x = 0.0, y = 0.0]

jshell> affine.transform(740, 1000)
$5 ==> Point2D [x = 320.0, y = 0.0]

jshell> affine.transform(740, 600)
$6 ==> Point2D [x = 320.0, y = 200.0]

jshell> affine.transform(100, 600)
$7 ==> Point2D [x = 0.0, y = 200.0]

jshell>

Cette fois, j'ai essayé d'entrer directement la valeur de coordonnée x et la valeur de coordonnée y au lieu de l'instance Point2D comme entrée de conversion.

Le système de coordonnées de données (100, 1000) a été converti en système de coordonnées d'écran (0, 0). Le système de coordonnées de données (740, 1000) a été converti en système de coordonnées d'écran (320, 0). Le système de coordonnées de données (740, 600) a été converti en système de coordonnées d'écran (320, 200). Le système de coordonnées de données (100, 600) a été converti en système de coordonnées d'écran (0, 200).

Conversion de coordonnées (6): agrandissement / réduction au centre de l'écran

Dans l'agrandissement / réduction de la conversion des coordonnées jusqu'à présent, le coin supérieur gauche de l'écran est utilisé comme point de base. Ensuite, jetons un coup d'œil à l'affichage d'un exemple de programme Canvas qui implémente jusqu'à présent la transformation de coordonnées. Si vous passez de l'affichage (1) à l'affichage (3), vous pouvez voir que l'affichage est basé sur le coin supérieur gauche.

Affichage (1)
Affichage (2)
Affichage (3)

Cependant, comme opération intuitive, je voudrais que vous zoomiez en avant et en arrière avec le centre de l'écran comme point de base.

Par conséquent, cette fois, nous ajouterons un mouvement parallèle qui déplace les coordonnées du coin supérieur gauche de l'écran vers le centre de l'écran dans le système de coordonnées de l'écran.

Tout d'abord, la formule de la transformation de coordonnées utilisée dans "Transformation de coordonnées (5): agrandissement / réduction et mouvement parallèle" est à nouveau répertoriée.

\begin{align*}
x' &= sx - sx_1 \\
y' &= -sy + sy_1
\end{align*}

Soit w la largeur de l'écran et h la hauteur de l'écran. La formule de conversion des coordonnées pour l'opération de déplacement du coin supérieur gauche de l'écran parallèlement au centre de l'écran est la suivante.

\begin{align*}
x'' &= x' + \frac{w}{2}\\
y'' &= y' + \frac{h}{2}
\end{align*}

La formule de conversion de coordonnées qui ajoute l'opération pour déplacer le coin supérieur gauche de l'écran parallèlement au centre de l'écran est la suivante.

\begin{align*}
x'' &= sx - sx_1 + \frac{w}{2}\\
y'' &= -sy + sy_1 + \frac{h}{2}
\end{align*}

Etant donné que le mouvement parallèle selon la taille de l'écran n'est pas affecté par la mise à l'échelle du système de coordonnées de données, le facteur de mise à l'échelle s n'est pas appliqué comme dans la formule ci-dessus.

La figure est illustrée ci-dessous.

データ座標→画面座標（画面中心）.png

La transformation affine est exprimée par l'expression de matrice suivante.

\begin{pmatrix}
s & 0 & -sx_1 + \frac{w}{2}\\
0 & -s & sy_1 + \frac{h}{2}\\
0 & 0 & 1
\end{pmatrix}

Expérimentation d'Affine dans l'environnement jshell du JDK 9

Lorsque la taille de l'écran est 320x200, la coordonnée du coin supérieur gauche de la zone de dessin dans le système de coordonnées de données est (200, 500) et l'échelle est 2.

jshell> affine = new Affine(2, 0, -240, 0, -2, 1100)
affine ==> Affine [
        2.0, 0.0, 0.0, -240.0
        0.0, -2.0, 0.0, 1100.0
        0.0, 0.0, 1.0, 0.0
]

jshell> affine.transform(200, 500)
$12 ==> Point2D [x = 160.0, y = 100.0]

Et vous pouvez voir que le coin supérieur gauche (200, 500) du système de coordonnées de données a été converti en (160, 100) dans le système de coordonnées d'écran et au centre de l'écran.

Lorsque la taille de l'écran est de 320 x 200, la coordonnée du coin supérieur gauche de la zone de dessin dans le système de coordonnées de données est (200, 500) et l'échelle est de 0,5.

jshell> affine = new Affine(0.5, 0, 60, 0, -0.5, 350)
affine ==> Affine [
        0.5, 0.0, 0.0, 60.0
        0.0, -0.5, 0.0, 350.0
        0.0, 0.0, 1.0, 0.0
]

jshell> affine.transform(200, 500)
$14 ==> Point2D [x = 160.0, y = 100.0]

Et vous pouvez voir que le coin supérieur gauche (200, 500) du système de coordonnées de données a été converti en (160, 100) dans le système de coordonnées d'écran et au centre de l'écran.

Résumé

Les transformations affines utilisées pour afficher les données définies dans le système de coordonnées orthogonales droitier à l'écran sont les suivantes:

\begin{pmatrix}
s & 0 & -sx_1 + \frac{w}{2}\\
0 & -s & sy_1 + \frac{h}{2}\\
0 & 0 & 1
\end{pmatrix}

cependant,\\
s est le taux d'expansion\\
(x_1, y_1)Les coordonnées des données à afficher au centre de l'écran\\
(w, h)Est la largeur et la hauteur de la taille d'affichage dans le système de coordonnées de l'écran

Référence / informations connexes

L'exemple de programme d'affichage d'écran sur JavaFX Canvas utilisant cette conversion affine et son explication sont décrits ci-dessous.

[Opération de dessin vectoriel et de mise à l'échelle du mouvement à l'aide de JavaFX Canvas](http://www.torutk.com/projects/swe/wiki/JavaFX_Canvas%E3%82%92%E4%BD%BF%E3%81% A3% E3% 81% 9F% E3% 83% 99% E3% 82% AF% E3% 82% BF% E3% 83% BC% E6% 8F% 8F% E7% 94% BB% E3% 81% A8% E6% 8B% A1% E5% A4% A7% E7% B8% AE% E5% B0% 8F% E7% A7% BB% E5% 8B% 95% E6% 93% 8D% E4% BD% 9C)

Les diapositives présentées au JJUG CCC 2016 Fall, qui m'ont inspiré pour écrire cet article, sont les suivantes.

Un blog qui a écrit que j'étais impliqué dans la conversion Affin avec Canvas dans le passé

La conversion affine avec Canvas convient beaucoup (je n'avais pas assez de sens mathématique ...)

Agrandir / réduire et mouvement parallèle avec JavaFX Canvas (Revenge)

introduction

Environnement d'exécution de cet article

Système de coordonnées de données et système de coordonnées d'écran

Lors de l'affichage des données cartographiques sans conversion ...

Conversion du système de coordonnées de données en système de coordonnées d'écran par conversion Affin

Transformation de coordonnées (1): transformation uniforme

Expérimentation d'Affine dans l'environnement jshell du JDK 9

Conversion de coordonnées (2): élimination de la tête en bas

Expérimentation d'Affine dans l'environnement jshell du JDK 9

Conversion de coordonnées (3): mouvement parallèle d'origine

Expérimentation d'Affine dans l'environnement jshell du JDK 9

Conversion de coordonnées (4): déplacer la zone de dessin

Expérimentation d'Affine dans l'environnement jshell du JDK 9

Conversion de coordonnées (5): mise à l'échelle et mouvement parallèle

En cas de grossissement 2 et mouvement parallèle (0, 100)

Exemple avec un grossissement de 0,5 et un mouvement parallèle (100, 1000)

Conversion de coordonnées (6): agrandissement / réduction au centre de l'écran

Expérimentation d'Affine dans l'environnement jshell du JDK 9

Résumé

Référence / informations connexes